Найти локальные максимумы
pks = findpeaks(data)data. Локальный пик является выборкой данных, которая либо больше, чем ее две соседние выборки, либо равна Inf. Не- Inf конечные точки сигнала исключены. Если пик плоский, функция возвращает только точку с самым низким индексом.
[___] = findpeaks(___, задает опции, использующие аргументы пары "имя-значение" в дополнение к любому из входных параметров в предыдущих синтаксисах.Name,Value)
findpeaks(___) без выходных аргументов строит график сигнала и накладывает пиковые значения.
Задайте вектор с тремя пиками и постройте график.
data = [25 8 15 5 6 10 10 3 1 20 7]; plot(data)

Найдите локальные максимумы. Peaks выводятся в порядке вхождения. Первая выборка не включена, несмотря на то, что является максимальным. Для плоского пика функция возвращает только точку с самым низким индексом.
pks = findpeaks(data)
pks = 1×3
15 10 20
Использование findpeaks без выходные аргументы для отображения peaks.
findpeaks(data)

Создайте сигнал, который состоит из суммы кривых колокола. Укажите местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [3 4 4 2 2 3]; Wdt = [2 6 3 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
Постройте график отдельных кривых и их суммы.
plot(x,Gauss,'--',x,PeakSig)
Использование findpeaks с настройками по умолчанию, чтобы найти peaks сигнала и их местоположения.
[pks,locs] = findpeaks(PeakSig,x);
Постройте график peaks с помощью findpeaks и пометьте их.
findpeaks(PeakSig,x) text(locs+.02,pks,num2str((1:numel(pks))'))

Отсортируйте peaks от самых высоких до самых коротких.
[psor,lsor] = findpeaks(PeakSig,x,'SortStr','descend'); findpeaks(PeakSig,x) text(lsor+.02,psor,num2str((1:numel(psor))'))

Создайте сигнал, который состоит из суммы кривых колокола, катающихся на полном периоде косинуса. Укажите местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); base = 4*cos(2*pi*x); Pos = [1 2 3 5 7 8]/10; Hgt = [3 7 5 5 4 5]; Wdt = [1 3 3 4 2 3]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss)+base;
Постройте график отдельных кривых и их суммы.
plot(x,Gauss,'--',x,PeakSig,x,base)
Использование findpeaks для определения местоположения и построения peaks, которые имеют известность не менее 4.
findpeaks(PeakSig,x,'MinPeakProminence',4,'Annotate','extents')

Самый высокий и самый низкий peaks являются единственными таковыми, которые удовлетворяют условию.
Отобразите проминенции и ширины на половинном значении всего peaks.
[pks,locs,widths,proms] = findpeaks(PeakSig,x); widths
widths = 1×6
0.0154 0.0431 0.0377 0.0625 0.0274 0.0409
proms
proms = 1×6
2.6816 5.5773 3.1448 4.4171 2.9191 3.6363
Солнечные пятна являются циклическим явлением. Их число, как известно, достигает максимума примерно каждые 11 лет.
Загрузите файл sunspot.dat, которая содержит среднее количество солнечных пятен, наблюдаемых каждый год с 1700 по 1987 год. Найдите и постройте график максимумов.
load sunspot.dat
year = sunspot(:,1);
avSpots = sunspot(:,2);
findpeaks(avSpots,year)
Улучшите свою оценку длительности цикла, игнорируя peaks, которые очень близки друг к другу. Найдите и постройте график peaks снова, но теперь ограничьте приемлемые разделения пик-пик значениями более шести лет.
findpeaks(avSpots,year,'MinPeakDistance',6)
Используйте пиковые местоположения, возвращенные findpeaks для вычисления среднего интервала между максимумами.
[pks,locs] = findpeaks(avSpots,year,'MinPeakDistance',6);
meanCycle = mean(diff(locs))meanCycle = 10.9600
Создайте datetime массив с использованием данных года. Предположим, что солнечные пятна подсчитывались каждый год 20 марта, близко к весеннему равноденствию. Найдите пик солнечного пятна лет. Используйте years функция, чтобы задать минимальное разделение пиков как duration.
ty = datetime(year,3,20); [pk,lk] = findpeaks(avSpots,ty,'MinPeakDistance',years(6)); plot(ty,avSpots,lk,pk,'o')

Вычислите среднее значение цикла солнечного пятна с помощью datetime функциональность.
dttmCycle = years(mean(diff(lk)))
dttmCycle = 10.9600
Составьте расписание с данными. Задайте переменную времени в годах. Постройте график данных. Отображение последних пяти записей расписания.
TT = timetable(years(year),avSpots); plot(TT.Time,TT.Variables)

entries = TT(end-4:end,:)
entries=5×1 timetable
Time avSpots
________ _______
1983 yrs 66.6
1984 yrs 45.9
1985 yrs 17.9
1986 yrs 13.4
1987 yrs 29.3
Загрузите аудиосигнал, дискретизированный с частотой 7418 Гц. Выберите 200 выборки.
load mtlb
select = mtlb(1001:1200);Найдите peaks, которые разделены не менее чем на 5 мс.
Чтобы применить это ограничение, findpeaks выбирает самый высокий пик в сигнале и устраняет весь peaks в пределах 5 мс от него. Функция затем повторяет процедуру для самого высокого оставшегося пика и итерация до тех пор, пока у нее не закончатся peaks, которые нужно учитывать.
findpeaks(select,Fs,'MinPeakDistance',0.005)
Найдите peaks, которые имеют амплитуду не менее 1 В.
findpeaks(select,Fs,'MinPeakHeight',1)
Найдите peaks, которые по крайней мере на 1 В выше, чем их соседние выборки.
findpeaks(select,Fs,'Threshold',1)
Найдите peaks, которые падают по крайней мере на 1 В с каждой стороны, прежде чем сигнал достигнет более высокого значения.
findpeaks(select,Fs,'MinPeakProminence',1)
Датчики могут возвращать отсеченные показания, если данные больше заданной точки насыщения. Вы можете принять решение игнорировать эти пики как бессмысленные или включить их в свой анализ.
Сгенерируйте сигнал, который состоит из продукта тригонометрических функций частот 5 Гц и 3 Гц, встроенных в белый Гауссов шум отклонения 0,1 ². Сигнал дискретизируется в течение одной секунды со скоростью 100 Гц. Сбросьте генератор случайных чисел для воспроизводимых результатов.
rng default
fs = 1e2;
t = 0:1/fs:1-1/fs;
s = sin(2*pi*5*t).*sin(2*pi*3*t)+randn(size(t))/10;Симулируйте насыщенное измерение путем усечения каждого показания, которое больше заданной границы 0,32. Постройте график насыщенного сигнала.
bnd = 0.32;
s(s>bnd) = bnd;
plot(t,s)
xlabel('Time (s)')
Определите местоположение peaks сигнала. findpeaks сообщает только переднее ребро каждого плоского пика.
[pk,lc] = findpeaks(s,t); hold on plot(lc,pk,'x')

Используйте 'Threshold' Пара "имя-значение", чтобы исключить плоский peaks. Требовать минимальное различие амплитуды между пиком и его соседями.
[pkt,lct] = findpeaks(s,t,'Threshold',1e-4); plot(lct,pkt,'o','MarkerSize',12)

Создайте сигнал, который состоит из суммы кривых колокола. Укажите местоположение, высоту и ширину каждой кривой.
x = linspace(0,1,1000); Pos = [1 2 3 5 7 8]/10; Hgt = [4 4 2 2 2 3]; Wdt = [3 8 4 3 4 6]/100; for n = 1:length(Pos) Gauss(n,:) = Hgt(n)*exp(-((x - Pos(n))/Wdt(n)).^2); end PeakSig = sum(Gauss);
Постройте график отдельных кривых и их суммы.
plot(x,Gauss,'--',x,PeakSig)
grid
Измерьте ширины peaks, используя половинную известность как ссылку.
findpeaks(PeakSig,x,'Annotate','extents')

Еще раз измерьте ширину, на этот раз используя половину высоты в качестве опорной.
findpeaks(PeakSig,x,'Annotate','extents','WidthReference','halfheight') title('Signal Peak Widths')

data - Входные данныеВходные данные, заданные как вектор. data должен быть реальным и должен иметь по крайней мере три элемента.
Типы данных: double | single
x - Расположениеdatetime массивМестоположения, заданные как вектор или datetime массив. x должен увеличиться монотонно и иметь ту же длину, что и data. Если x опускается, тогда индексы data используются как местоположения.
Типы данных: double | single | datetime
Fs - Частота дискретизацииЧастота дискретизации, заданная как положительная скалярная величина. Частота дискретизации является количеством выборок в единицу времени. Если модулем времени является секунды, частота дискретизации имеет модули измерения hertz.
Типы данных: double | single
Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.
'SortStr','descend','NPeaks',3 находит три самых высоких peaks сигнала.'NPeaks' - Максимальное количество peaksМаксимальное количество peaks, заданное как разделенная разделенными запятой парами, состоящая из 'NPeaks' и положительный целочисленный скаляр. findpeaks действует от первого элемента входных данных и заканчивается, когда количество peaks достигает значения 'NPeaks'.
Типы данных: double | single
'SortStr' - Пиковая сортировка'none' (по умолчанию) | 'ascend' | 'descend'Пиковая сортировка, заданная как разделенная разделенными запятой парами, состоящая из 'SortStr' и одно из следующих значений:
'none' возвращает peaks в том порядке, в котором они происходят во входных данных.
'ascend' возвращает peaks в порядке возрастания или увеличения от наименьшего до наибольшего значения.
'descend' возвращает peaks в порядке убывания от наибольшего до наименьшего значения.
'MinPeakHeight' - Минимальная высота пика-Inf (по умолчанию) | действительный скалярМинимальная пиковая высота, заданная как разделенная разделенными запятой парами, состоящая из 'MinPeakHeight' и настоящий скаляр. Используйте этот аргумент для findpeaks возвращают только те пики выше 'MinPeakHeight'. Установка минимальной высоты пика может сократить время вычислений.
Типы данных: double | single
'MinPeakProminence' - Минимальная пиковая известностьМинимальная пиковая известность, заданная как разделенная разделенными запятой парами, состоящая из 'MinPeakProminence' и настоящий скаляр. Используйте этот аргумент для findpeaks возвращают только те пики, которые имеют относительную важность как минимум 'MinPeakProminence'. Для получения дополнительной информации смотрите Prominence.
Типы данных: double | single
'Threshold' - Минимальное различие высотМинимальное различие высот между пиком и его соседями, заданная как разделенная разделенными запятой парами, состоящая из 'Threshold' и неотрицательный действительный скаляр. Используйте этот аргумент для findpeaks возвращают только те пики, которые превышают их непосредственные соседние значения по крайней мере на значение 'Threshold'.
Типы данных: double | single
'MinPeakDistance' - Минимальное пиковое разделениеМинимальное разделение пиков, заданное как разделенная разделенными запятой парами, состоящая из 'MinPeakDistance' и положительный действительный скаляр. Когда вы задаете значение для 'MinPeakDistance'алгоритм выбирает самый высокий пик в сигнале и игнорирует весь peaks в 'MinPeakDistance' его. Функция затем повторяет процедуру для самого высокого оставшегося пика и итерация до тех пор, пока у нее не закончатся peaks, которые нужно учитывать.
Если вы задаете вектор местоположения, x, затем 'MinPeakDistance' должны быть выражены в терминах x. Если x является datetime массив, затем задайте 'MinPeakDistance' как duration скаляром или как числовым скаляром, выраженной в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MinPeakDistance' должно быть выражено в единицах времени.
Если вы не задаете ни одного xни Fs, затем 'MinPeakDistance' должны быть выражены в единицах выборок.
Используйте этот аргумент для findpeaks игнорируйте небольшой peaks, которые происходят в районе большей вершины.
Типы данных: double | single | duration
'WidthReference' - Базовая высота для измерений ширины'halfprom' (по умолчанию) | 'halfheight'Эталонная высота для измерений ширины, заданная как разделенная разделенными запятой парами, состоящая из 'WidthReference' и любой из них 'halfprom' или 'halfheight'. findpeaks оценивает ширину пика как расстояние между точками, где нисходящий сигнал перехватывает горизонтальную исходную линию. Высота линии выбирается с помощью критерия, заданного в 'WidthReference':
'halfprom' позиционирует ссылку линию под пиком на вертикальном расстоянии, равном половине пиковой известности. Смотрите Prominence для получения дополнительной информации.
'halfheight' позиционирует ссылку линию на половине высоты пика. Линия обрезается, если какая-либо из ее точек точки пересечения находится за границами выбранного peaks путем установки 'MinPeakHeight', 'MinPeakProminence', и 'Threshold'. Граница между peaks определяется горизонтальным положением самого низкого оврага между ними. Peaks с высотой менее нуля отбрасываются.
Местоположения точек точки пересечения вычисляются линейной интерполяцией.
'MinPeakWidth' - Минимальная пиковая ширинаМинимальная пиковая ширина, заданная как разделенная разделенными запятой парами, состоящая из 'MinPeakWidth' и положительный действительный скаляр. Используйте этот аргумент, чтобы выбрать только те пики, которые имеют ширину не менее 'MinPeakWidth'.
Если вы задаете вектор местоположения, x, затем 'MinPeakWidth' должны быть выражены в терминах x. Если x является datetime массив, затем задайте 'MinPeakWidth' как duration скаляром или как числовым скаляром, выраженной в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MinPeakWidth' должно быть выражено в единицах времени.
Если вы не задаете ни одного xни Fs, затем 'MinPeakWidth' должны быть выражены в единицах выборок.
Типы данных: double | single | duration
'MaxPeakWidth' - Максимальная пиковая ширинаInf (по умолчанию) | положительный действительный скалярМаксимальная пиковая ширина, заданная как разделенная разделенными запятой парами, состоящая из 'MaxPeakWidth' и положительный действительный скаляр. Используйте этот аргумент для выбора только тех пиков, которые имеют ширину не более 'MaxPeakWidth'.
Если вы задаете вектор местоположения, x, затем 'MaxPeakWidth' должны быть выражены в терминах x. Если x является datetime массив, затем задайте 'MaxPeakWidth' как duration скаляром или как числовым скаляром, выраженной в днях.
Если вы задаете частоту дискретизации, Fs, затем 'MaxPeakWidth' должно быть выражено в единицах времени.
Если вы не задаете ни одного xни Fs, затем 'MaxPeakWidth' должны быть выражены в единицах выборок.
Типы данных: double | single | duration
'Annotate' - Стиль графика'peaks' (по умолчанию) | 'extents'Стиль графика, заданный как разделенная разделенными запятой парами, состоящая из 'Annotate' и одно из следующих значений:
'peaks' строит график сигнала и аннотирует местоположение и значение каждого пика.
'extents' строит график сигнала и аннотирует местоположение, значение, ширину и известность каждого пика.
Этот аргумент игнорируется, если вы вызываете findpeaks с выходными аргументами.
pks - Локальные максимумыЛокальные максимумы, возвращенные как вектор значений сигналов. Если локальных максимумов нет, то pks пуст.
locs - Пиковые местоположенияПиковые местоположения, возвращенные как вектор.
Если вы задаете вектор местоположения, x, затем locs содержит значения x в пиковых индексах.
Если вы задаете частоту дискретизации, Fs, затем locs является числовым вектором моментов времени с временного различия 1/ Fs между последовательными выборками.
Если вы не задаете ни одного xни Fs, затем locs является вектором целочисленных индексов.
w - Пиковые шириныПиковые ширины, возвращенные как вектор вещественных чисел. Ширина каждого пика вычисляется как расстояние между точками слева и справа от пика, где сигнал перехватывает ссылку линии, высота которого задана WidthReference. Сами точки находят путем линейной интерполяции.
p - Peak prominencesПиковые проминенции, возвращенные как вектор вещественных чисел. Известность пика является минимальным вертикальным расстоянием, которое сигнал должен опуститься с каждой стороны пика, прежде чем подняться назад на уровень выше пика или достигнуть конечной точки. Смотрите Prominence для получения дополнительной информации.
Известность пика измеряет, насколько пик выделяется из-за собственной высоты и расположения относительно другого peaks. Низкий изолированный пик может быть более заметным, чем тот, который выше, но в противном случае является ничем не примечательным представитель высокой области значений.
Чтобы измерить известность пика:
Поместите маркер на пик.
Удлините горизонтальную линию от пика налево и вправо, пока линия не сделает одно из следующих:
Пересекает сигнал, потому что существует более высокий пик
Достигает левого или правого конца сигнала
Найдите минимум сигнала в каждом из двух интервалов, определенных на шаге 2. Эта точка является или оврагом, или одной из сигнальных конечных точек.
Более высокий из двух минимумов интервала задает уровень ссылки. Высота пика над этим уровнем является его известностью.
findpeaks не делает никаких предположений о поведении сигнала за пределами его конечных точек, независимо от их высоты. Это отражено на шагах 2 и 4 и часто влияет на значение опорного уровня. Рассмотрим, например, peaks этого сигнала:
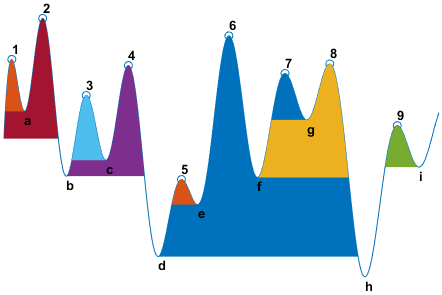
| Пиковое число | Левый интервал лежит между пиками | Правый интервал лежит между пиками | Самая низкая точка левого интервала | Самая низкая точка правого интервала | Эталонный уровень (наивысший минимум) |
|---|---|---|---|---|---|
| 1 | Левый конец | Пересечение из-за пика 2 | Левая конечная точка | a | a |
| 2 | Левый конец | Правый конец | Левая конечная точка | h | Левая конечная точка |
| 3 | Пересечение из-за пика 2 | Пересечение из-за пика 4 | b | c | c |
| 4 | Пересечение из-за пика 2 | Пересечение из-за пика 6 | b | d | b |
| 5 | Пересечение из-за пика 4 | Пересечение из-за пика 6 | d | e | e |
| 6 | Пересечение из-за пика 2 | Правый конец | d | h | d |
| 7 | Пересечение из-за пика 6 | Пересечение из-за пика 8 | f | g | g |
| 8 | Пересечение из-за пика 6 | Правый конец | f | h | f |
| 9 | Пересечение из-за пика 8 | Пересечение из-за правой конечной точки | h | я | я |
fminbnd | fminsearch | fzero | islocalmax | islocalmin | max
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.