Обратное кратковременное преобразование Фурье
x = istft(___,Name,Value)
Сгенерируйте трехканальный сигнал, состоящий из трех различных щебетов, дискретизированных с частотой 1 кГц в течение 1 секунды.
Первый канал состоит из вогнутого квадратичного щебета с мгновенной частотой 100 Гц при t = 0 и пересекает 300 Гц при t = 1 секунде. Начальная фаза равна 45 степеням.
Второй канал состоит из выпуклого квадратичного щебета с мгновенной частотой 200 Гц при t = 0 и пересекает 600 Гц при t = 1 секунде.
Третий канал состоит из логарифмического щебета с мгновенной частотой 300 Гц при t = 0 и пересекает 500 Гц при t = 1 секунде.
Вычислите STFT многоканального сигнала с помощью периодического окна Хэмминга длины 256 и длины перекрытия 15 выборки.
fs = 1e3; t = 0:1/fs:1-1/fs; x = [chirp(t,100,1,300,'quadratic',45,'concave'); chirp(t,200,1,600,'quadratic',[],'convex'); chirp(t,300,1,500,'logarithmic')]'; [S,F,T] = stft(x,fs,'Window',hamming(256,'periodic'),'OverlapLength',15);
Постройте график оригинальной и реконструированной версий первого и второго каналов.
[ix,ti] = istft(S,fs,'Window',hamming(256,'periodic'),'OverlapLength',15); plot(t,x(:,1)','LineWidth',1.5) hold on plot(ti,ix(:,1)','r--') hold off legend('Original Channel 1','Reconstructed Channel 1')

plot(t,x(:,2)','LineWidth',1.5) hold on plot(ti,ix(:,2)','r--') legend('Original Channel 2','Reconstructed Channel 2')

Вокодер фазы выполняет растяжение во времени и масштабирование тангажа путем преобразования аудио в частотный диапазон. Эта схема показывает операции, участвующие в реализации фазы вокодера.

Фазовый вокодер принимает STFT сигнала с окном анализа размера скачка а затем выполняет ISTFT с окном синтеза размера скачка . Таким образом, вокодер использует в своих интересах метод WOLA. Чтобы растянуть сигнал во времени, в окне анализа используется большее количество выборок перекрытия, чем синтез. В результате на выходе больше выборок, чем на входе (), хотя содержимое остается неизменным. Теперь можно поднять шкалу этого сигнала путем воспроизведения его с более высокой частотой дискретизации, которая выдает сигнал с исходной длительностью, но с более высоким тангажом.
Загрузите аудио файла, содержащее фрагмент Hallelujah Chorus Генделя, выбранный с частотой дискретизации 8192 Гц.
load handelСпроектируйте окно корня-Ханна длиной 512. Установите длину перекрытия анализа равную 192, и длину перекрытия синтеза равную 166.
wlen = 512;
win = sqrt(hann(wlen,'periodic'));
noverlapA = 192;
noverlapS = 166;Реализуйте фазовый вокодер с помощью окна анализа перекрытия 192 и окна синтеза перекрытия 166.
S = stft(y,Fs,'Window',win,'OverlapLength',noverlapA); iy = istft(S,Fs,'Window',win,'OverlapLength',noverlapS); %To hear, type soundsc(w,Fs), pause(10), soundsc(iw,Fs);
Если окна анализа и синтеза совпадают, но длина перекрытия изменена, будет дополнительная прибыль/потеря, которую вам нужно будет настроить. Это общий подход к реализации фазы вокодера.
Вычислите коэффициент скачка и используйте его, чтобы настроить усиление восстановленного сигнала. Также вычислите частоту сдвинутых по тангажу данных с помощью коэффициента скачка.
hopRatio = (wlen-noverlapS)/(wlen-noverlapA);
iyg = iy*hopRatio;
Fp = Fs*hopRatio;
%To hear, type soundsc(iwg,Fs), pause(15), soundsc(iwg,Fp);Постройте график исходного сигнала и растянутого по времени сигнала с фиксированным усилением.
plot((0:length(iyg)-1)/Fs,iyg,(0:length(y)-1)/Fs,y) xlabel('Time (s)') xlim([0 (length(iyg)-1)/Fs]) legend('Time Stretched Signal with Fixed Gain','Original Signal','Location','best')

Сравните растянутый по времени сигнал и сдвинутый по тангажу сигнал на том же графике.
plot((0:length(iy)-1)/Fs,iy,(0:length(iy)-1)/Fp,iy) xlabel('Time (s)') xlim([0 (length(iyg)-1)/Fs]) legend('Time Stretched Signal','Pitch Shifted Signal','Location','best')

Чтобы лучше понять эффект данных перемены тангажа, рассмотрите следующую синусоиду частоты Fs более 2 секунд.
t = 0:1/Fs:2; x = sin(2*pi*10*t);
Вычислите короткое преобразование Фурье и обратное короткое преобразование Фурье с длинами перекрытия 192 и 166 соответственно.
Sx = stft(x,Fs,'Window',win,'OverlapLength',noverlapA); ix = istft(Sx,Fs,'Window',win,'OverlapLength',noverlapS);
Постройте график исходного сигнала на одном графике и растянутого по времени и смещенного по тангажу сигнала на другом.
subplot(2,1,1) plot((0:length(ix)-1)/Fs,ix,'LineWidth',2) xlabel('Time (s)') ylabel('Signal Amplitude') xlim([0 (length(ix)-1)/Fs]) legend('Time Stretched Signal') subplot(2,1,2) hold on plot((0:length(x)-1)/Fs,x) plot((0:length(ix)-1)/Fp,ix,'--','LineWidth',2) legend('Original Signal','Pitch Shifted Signal','Location','best') hold off xlabel('Time (s)') ylabel('Signal Amplitude') xlim([0 (length(ix)-1)/Fs])

Сгенерируйте комплексную синусоиду частоты 1 кГц и длительности 2 секунды.
fs = 1e3; ts = 0:1/fs:2-1/fs; x = exp(2j*pi*100*cos(2*pi*2*ts));
Проектируйте периодическое окно Ханна длиной 100 и установите количество выборок перекрытия равным 75. Проверьте длину окна и перекрытия для податливости COLA.
nwin = 100;
win = hann(nwin,'periodic');
noverlap = 75;
tf = iscola(win,noverlap)tf = logical
1
Обнулите сигнал, чтобы удалить эффекты края. Чтобы избежать усечения, дополните входной сигнал нулями так, чтобы
- целое число. Установите длину БПФ равной 128. Вычислите кратковременное преобразование Фурье комплексного сигнала.
nPad = 100; xZero = [zeros(1,nPad) x zeros(1,nPad)]; fftlen = 128; s = stft(xZero,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);
Вычислите обратное кратковременное преобразование Фурье и удалите нули для идеальной реконструкции.
[is,ti] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen); is(1:nPad) = []; is(end-nPad+1:end) = []; ti = ti(1:end-2*nPad);
Постройте график реальных частей исходных и восстановленных сигналов. Мнимая часть сигнала также прекрасно реконструирована.
plot(ts,real(x)) hold on plot(ti,real(is),'--') xlim([0 0.5]) xlabel('Time (s)') ylabel('Amplitude (V)') legend('Original Signal','Reconstructed Signal') hold off

Сгенерируйте синусоиду, отобранную с частотой дискретизации 2 кГц в течение 1 секунды.
fs = 2e3; t = 0:1/fs:1-1/fs; x = 5*sin(2*pi*10*t);
Проектируйте периодическое окно Хэмминга длины 120. Проверьте ограничение COLA для окна с перекрытием 80 выборок. Комбинация оконного перекрытия совместима с COLA.
win = hamming(120,'periodic');
noverlap = 80;
tf = iscola(win,noverlap)tf = logical
1
Установите длину БПФ равной 512. Вычислите кратковременное преобразование Фурье.
fftlen = 512; s = stft(x,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen);
Вычислите обратное кратковременное преобразование Фурье.
[X,T] = istft(s,fs,'Window',win,'OverlapLength',noverlap,'FFTLength',fftlen,'Method','ola','ConjugateSymmetric',true);
Постройте график исходных и восстановленных сигналов.
plot(t,x,'b') hold on plot(T,X,'-.r') xlabel('Time (s)') ylabel('Amplitude (V)') title('Original and Reconstructed Signal') legend('Original Signal','Reconstructed Signal') hold off

s - Короткое преобразование ФурьеКратковременное преобразование Фурье, заданное как матрица или трехмерный массив. Для одноканальных сигналов задайте s как матрица с увеличением времени по столбцам и увеличением частоты вниз по строкам. Для многоканальных сигналов задайте s как трехмерный массив с третьей размерностью, соответствующим каналам. Частота и временные векторы получаются как выходы stft.
Примечание
Если вы инвертируете s использование istft и хотите, чтобы результат был такой же длины, как и x, значение (length(x)-noverlap)/(length(window)-noverlap) должно быть целым числом.
Типы данных: double | single
Поддержка комплексного числа: Да
fs - Частота дискретизации2π (по умолчанию) | положительная скалярная величинаЧастота дискретизации в герцах, заданная как положительная скалярная величина.
Типы данных: double | single
ts - Шаг расчетаШаг расчета, заданный как duration скаляр.
Пример: seconds(1) является duration
Типы данных: duration
Задайте необязательные разделенные разделенными запятой парами Name,Value аргументы. Name - имя аргумента и Value - соответствующее значение. Name должны находиться внутри кавычек. Можно задать несколько аргументов в виде пар имен и значений в любом порядке Name1,Value1,...,NameN,ValueN.
istft(s,'Window',win,'OverlapLength',50,'FFTLength',128) окон данных с помощью окна winс 50 выборками перекрываются между смежными сегментами и 128 точками ДПФ.'Window' - Функция оконной обработкиhann(128,'periodic') (по умолчанию) | векторФункция окна, заданная как разделенная разделенными запятой парами, состоящая из 'Window' и вектор. Если вы не задаете окно или задаете его как пустой, функция использует периодическое окно Ханна длины 128. Длина Window должно быть больше или равно 2.
Список доступных окон см. в разделе Windows.
Пример: hann(N+1) и (1-cos(2*pi*(0:N)'/N))/2 оба задают окно Ханна длины N + 1.
Типы данных: double | single
'OverlapLength' - Количество перекрываемых выборок75% длины окна (по умолчанию) | неотрицательным целым числомКоличество перекрывающихся выборок, заданное как разделенная разделенными запятой парами, состоящая из 'OverlapLength' и положительное целое число, меньше длины window. Если вы опускаете 'OverlapLength' или укажите его как пустой, оно устанавливается на самое большое целое число менее 75% длины окна, что оказывается 96 выборками для окна Ханна по умолчанию.
Типы данных: double | single
'FFTLength' - Количество точек ДПФ128 (по умолчанию) | положительное целое числоКоличество точек ДПФ, заданное как разделенная разделенными запятой парами, состоящая из 'FFTLength' и положительное целое число. Чтобы достичь идеальной реконструкции во временной области, необходимо задать количество точек ДПФ, соответствующее тому, которое использовалось в stft.
Типы данных: double | single
'Method' - Метод перекрытия-добавления'wola' (по умолчанию) | 'ola'Метод наложения-сложения, заданный как разделенная разделенными запятой парами, состоящая из 'Method' и одно из следующего:
'wola' - Взвешенное перекрытие-добавить
'ola' - Наложение-добавление
'ConjugateSymmetric' - Сопряженная симметрия исходного сигналаfalse (по умолчанию) | trueСопряженная симметрия исходного сигнала, заданная как разделенная разделенными запятой парами, состоящая из 'ConjugateSymmetric' и true или false. Если для этой опции задано значение true, istft принимает, что входной s симметрично, в противном случае симметричное предположение не делается. Когда s не является точно сопряженным симметричным из-за ошибки округления, устанавливая паре "имя-значение" равной true обеспечивает обработку STFT как сопряженной симметрии. Если s является сопряженным симметричным, тогда расчет обратного преобразования происходит быстрее, и выход является вещественным.
'FrequencyRange' - частотная область значений STFT'centered' (по умолчанию) | 'twosided' | 'onesided'Область значений STFT, заданный как разделенная разделенными запятой парами, состоящая из 'FrequencyRange' и 'centered', 'twosided', или 'onesided'.
'centered' - Лечите s как двусторонний, центрированный STFT. Если nfft даже, тогда s считается вычисленным по интервалу (- π, π] рад/выборка. Если nfft нечетно, тогда s считается вычисленным по интервалу (- π, π) рад/выборка. Если вы задаете информацию о времени, то интервалы являются (- f s, f s/2] циклами/единичным временем и (- f s, f s/2) циклами/единичным временем, соответственно, где f s - частота дискретизации.
'twosided' - Лечите s как двусторонний STFT, вычисленный через интервал [0, 2 π) рад/отсчета. Если вы задаете информацию о времени, то интервал составляет [0, f с) циклов/единичное время.
'onesided' - Лечите s как односторонний STFT. Если nfft даже, тогда s считается вычисленным за интервал [0, π] рад/выборка. Если nfft нечетно, тогда s считается вычисленным за интервал [0, π) рад/выборка. Если вы задаете информацию о времени, то интервалы являются [0, f s/2] циклами/единичным временем и [0, f s/2) циклами/единичным временем, соответственно, где f s - частота дискретизации.
Примечание
Когда для этого аргумента задано значение 'onesided', istft принимает значения в положительной области значений Найквиста, которые были вычислены без сохранения общей степени.
Для получения примера смотрите STFT Frequency Областей значений.
Типы данных: char | string
'InputTimeDimension' - Входное измерение времени'acrosscolumns' (по умолчанию) | 'downrows'Входная размерность, заданный как разделенная разделенными запятой парами, состоящая из 'InputTimeDimension' и 'acrosscolumns' или 'downrows'. Если для этого значения задано значение 'downrows', istft принимает, что временная размерность s опускается вниз по строкам, и частота пересекает столбцы. Если для этого значения задано значение 'acrosscolumns', функцию istft принимает, что временная размерность s пересекает столбцы, и размерность вниз по строкам.
x - Восстановленный сигналВосстановленный сигнал во временном интервале, возвращенный как вектор или матрица.
Типы данных: single | double
t - Моменты времениМомент времени, возвращенный как вектор.
Типы данных: double | single
Обратное короткое преобразование Фурье вычисляется путем взятия ОБПФ каждого вектора DFT STFT и добавления-перекрытия инвертированных сигналов. ISTFT рассчитывается следующим образом:
где - размер скачка между последовательными ДПФ, - ДПФ оконных данных с центром во времени и . Обратный STFT является идеальной реконструкцией исходного сигнала, пока где analysis window использовался для окна исходного сигнала и является константой. Следующий рисунок изображает шаги, следующие при восстановлении исходного сигнала.
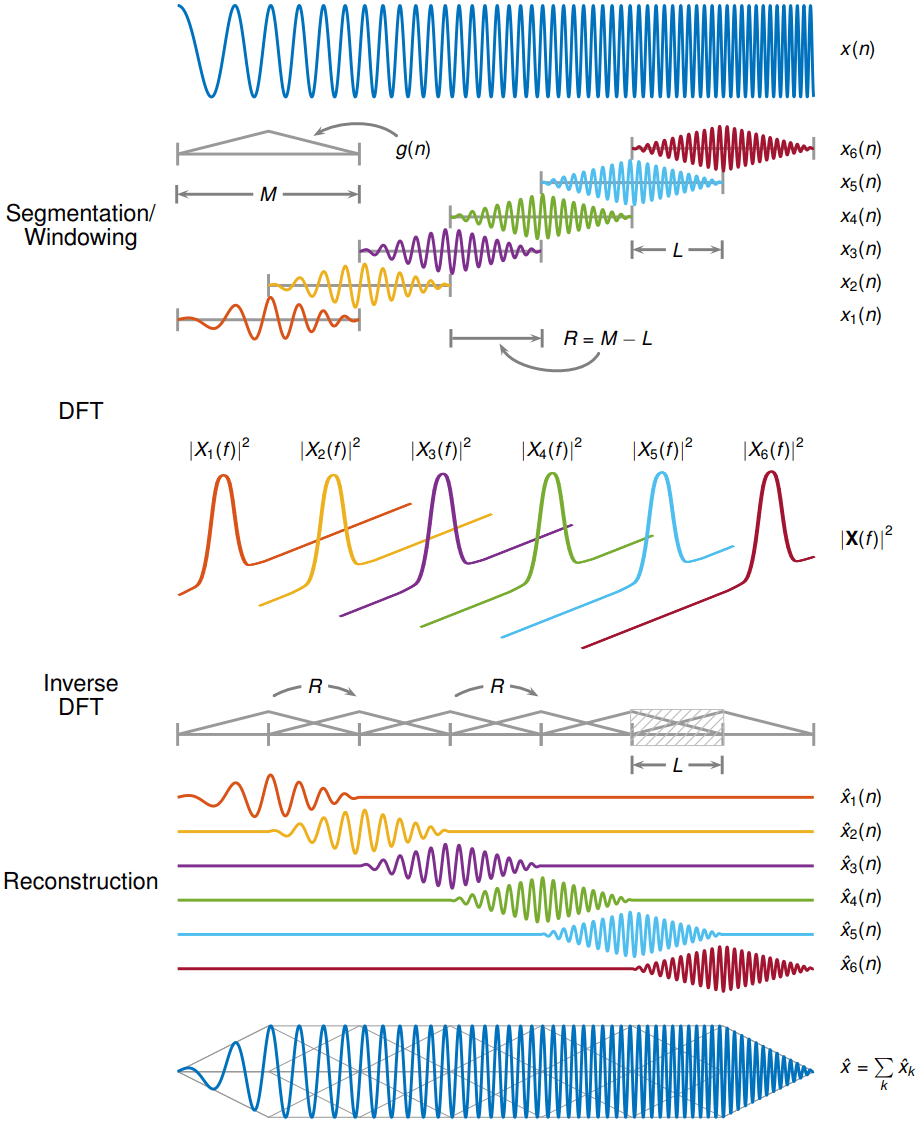
Чтобы гарантировать успешную реконструкцию немодифицированных спектров, окно анализа должно удовлетворять ограничению COLA. В целом, если окно анализа удовлетворяет условию окно считается совместимым с COLA. Кроме того, податливость COLA может быть описано как слабое или сильное.
Слабая податливость COLA подразумевает, что преобразование Фурье окна анализа имеет нули в гармониках частоты кадров, таких что
Подавление псевдонима нарушается спектральными модификациями. Слабая COLA полагается на отмену псевдонима в частотный диапазон. Поэтому возможна идеальная реконструкция с использованием слабо совместимых с COLA окон, пока сигнал не претерпел никаких спектральных модификаций.
Для сильной податливости COLA, преобразование Фурье окна должно быть ограничено последовательно с понижающей дискретизацией частотой систем координат, такой что
Это уравнение показывает, что никакое сглаживание не допускается сильным ограничением COLA. Кроме того, для сильной податливости COLA, значение константы должно равняться 1. В целом, если короткий спектр модифицирован каким-либо образом, предпочтительным является более сильное окно, совместимое с COLA.
Вы можете использовать iscola функция для проверки на слабую податливость COLA. Количество суммаций, используемых для проверки податливости COLA, определяется длиной окна и размером скачка. В целом, обычно использовать в для взвешенного наложения-сложения (WOLA), и для наложения-добавления (OLA). По умолчанию, istft использует метод WOLA, применяя synthesis window перед выполнением метода перекрытия-суммы.
В целом окно синтеза совпадает с окном анализа. Можно создать полезные окна WOLA, взяв квадратный корень сильного окна OLA. Можно использовать этот метод для всех неотрицательных окон OLA. Например, окно root-Hann является хорошим примером окна WOLA.
В целом вычисление STFT входного сигнала и инвертирование его не приводит к идеальной реконструкции. Если вы хотите, чтобы выход ISTFT максимально совпадал с исходным входным сигналом, сигнал и окно должны удовлетворять следующим условиям:
Вход - Если вы инвертируете выходной параметр stft использование istft и хотите, чтобы результат был такой же длины, как и входной сигнал x, значение должно быть целым числом.
Податливость COLA - Используйте совместимые с COLA окна, принимая, что вы не изменили краткосрочное преобразование Фурье сигнала.
Заполнение - Если длина входного сигнала такова, что значение k не является целым числом, обнулите сигнал перед вычислением кратковременного преобразования Фурье. Удалите дополнительные нули после инвертирования сигнала.
[1] Crochiere, R. E. «A Weighted Overlap-Add Method of Short-Time Fourier Analysis/Synthesis». Транзакции IEEE по акустике, обработке речи и сигналов. Том 28, № 1, февраль 1980, стр. 99-102.
[2] Готцен, А. Д., Н. Бернардини, и Д. Арфиб. Традиционные реализации фазового вокодера: трюки торговли. Материалы Конференции COST G-6 по цифровому аудио Эффектов (DAFX-00), Верона, Италия, 7-9 декабря 2000 года.
[3] Гриффин, Дэниел У. и Чжэ С. Лим. Оценка сигнала из модифицированного краткосрочного преобразования Фурье. Транзакции IEEE по акустике, обработке речи и сигналов. Том 32, № 2, апрель 1984, стр. 236-243.
[4] Портнофф, М. Р. «Представление временных частот цифровых сигналов и систем на основе кратковременного Фурье-анализа». Транзакции IEEE по акустике, обработке речи и сигналов. Том 28, № 1, фев 1980, стр. 55-69.
[5] Смит, Джулиус Орион. Спектральная обработка аудиосигнала. https://ccrma.stanford.edu/~jos/sasp/, онлайн книга, издание 2011, доступ к Nov. 2018.
[6] Шарп, Брюс. Обратимость обработки перекрытия-добавления. https://gauss256.github.io/blog/cola.html, доступ к июлю 2019 года.
Указания и ограничения по применению:
'InputTimeDimension' необходимо всегда задавать и устанавливать на 'downrows'.
Для получения дополнительной информации см. Раздел «Длинные массивы»
Указания и ограничения по применению:
The 'ConjugateSymmetric' аргумент не поддерживается для генерации кода.
Указания и ограничения по применению:
The 'ConjugateSymmetric' аргумент не поддерживается для генерации кода.
Указания и ограничения по применению:
Если только 'ConjugateSymmetric' установлено в true, а выход x всегда комплексно, даже если все мнимые части равны нулю.
Для получения дополнительной информации смотрите Запуск функций MATLAB на графическом процессоре (Parallel Computing Toolbox).
У вас есть измененная версия этого примера. Вы хотите открыть этот пример с вашими правками?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.