Документация

Зачем использовать Windows?

Как при создании цифровых фильтров, так и при спектральной оценке, выбор оконной функции может сыграть важную роль в определении качества общих результатов. Главная роль окна состоит в том, чтобы смочить эффекты феномена Гиббса, который возникает в результате усечения бесконечного ряда.

Доступные функции окна

Графические инструменты пользовательского интерфейса

Для работы с окнами в продукте Signal Processing Toolbox™ предусмотрены два графических инструмента интерфейса:

Для получения дополнительной информации см. страницы с описанием.

Основные формы

Основным окном является rectangular window, вектор из них соответствующей длины. Прямоугольное окно длины 50

n = 50;
w = rectwin(n);

Signal Processing Toolbox хранит окна в векторах-столбцах по соглашению, поэтому эквивалентное выражение является

w = ones(50,1);

Чтобы использовать приложение Window Designer для создания этого окна, введите

windowDesigner

Откроется приложение с окном Хэмминга по умолчанию. Чтобы визуализировать прямоугольное окно, установите Type = Rectangular и Length = 50 на панели «Информация о активном окне» и нажмите Apply.

Окно Бартлетта (или треугольное) является сверткой двух прямоугольных окон. Функции bartlett и triang вычислить аналогичные треугольные окна с тремя важными различиями. The bartlett функция всегда возвращает окно с двумя нулями на концах последовательности, так что для n odd, центральное сечение bartlett(n+2) эквивалентно triang(n):

Bartlett = bartlett(7);
isequal(Bartlett(2:end-1),triang(5))

ans =
     1

Для n четные, bartlett все еще является сверткой двух прямоугольных последовательностей. Для треугольного окна не существует стандартного определения n четные; склоны линии сегментов triang результат немного круче, чем у bartlett в этом случае:

w = bartlett(8); 
[w(2:7) triang(6)]

Вы можете увидеть различие между нечетными и даже окнами Бартлетта в Window Designer.

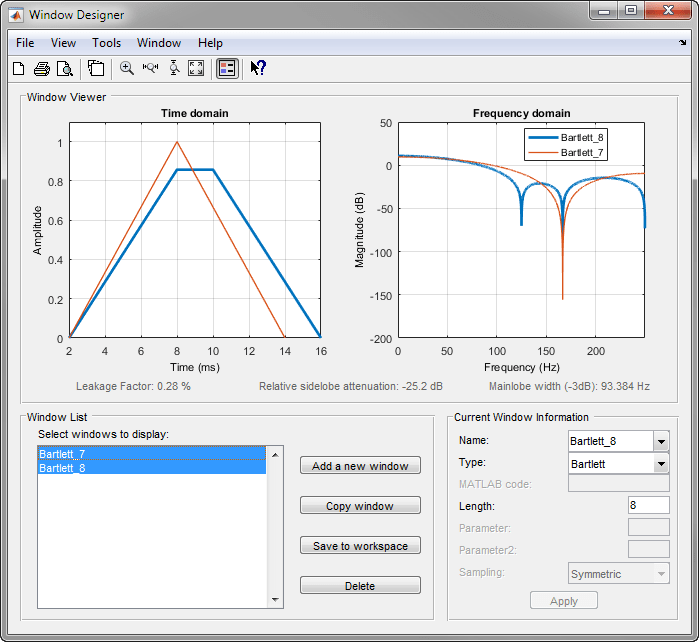
Окончательное различие между окнами Бартлетта и треугольными очевидно в преобразованиях Фурье этих функций. Преобразование Фурье окна Бартлетта отрицательно для n даже. Преобразование Фурье треугольного окна, однако, всегда неотрицательно.

Следующий рисунок, на котором изображены нулевые фазовые характеристики 8-точечных окон Бартлетта и Треугольные, иллюстрирует различие.

zerophase(bartlett(8))
hold on
zerophase(triang(8))
legend('Bartlett','Triangular')
axis([0.3 1 -0.2 0.5])

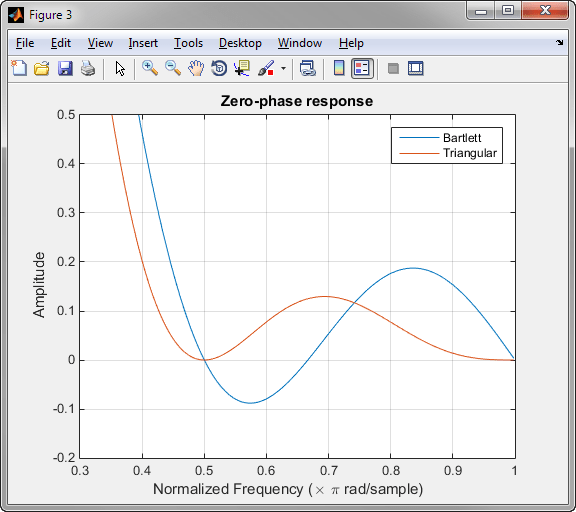
Это различие может быть важным при выборе окна для некоторых методов спектральной оценки, таких как метод Блэкмана-Тьюки. Блэкман-Тьюки формирует спектральную оценку путем вычисления преобразования Фурье автокорреляционной последовательности. Получившаяся оценка может быть отрицательной на некоторых частотах, если преобразование Фурье окна отрицательное.