Цифровые фильтры с конечной длительностью импульсной характеристики (все-нулевые, или конечная импульсная характеристика) имеют как преимущества, так и недостатки по сравнению с фильтрами с бесконечной длительностью импульсной характеристики (БИХ).
Конечная импульсная характеристика имеют следующие основные преимущества:
Основной недостаток конечных импульсных характеристик заключается в том, что они часто требуют гораздо более высокого порядка фильтра, чем БИХ, для достижения заданного уровня эффективности. Соответственно, задержка этих фильтров часто намного больше, чем для равной эффективности БИХ фильтра.
Конечная импульсная характеристика
Метод создания фильтра | Описание | Функции filter |
|---|---|---|
Работа с окнами | Применить окно к усеченному обратному преобразованию Фурье заданного фильтра «кирпичная стенка» | |
Мультиполосный с переходными полосами | Подход Equiripple или методом наименьших квадратов в поддиапазонах частотной области значений | |
Методы наименьших квадратов с ограничениями | Минимизируйте квадратную интегральную ошибку во всей частотной области значений, удовлетворяющем максимальным ограничениям по ошибкам | |
Произвольный ответ | Произвольные отклики, включая нелинейную фазу и комплексные фильтры | |
Приподнятый косинус | Lowpass с плавным, синусоидальным переходом |
Кроме cfirpmвсе конечные импульсные характеристики создания фильтра функции проектируют только линейные фильтры фазы. Коэффициенты фильтра, или «отводы», таких фильтров подчиняются либо четному, либо нечетному отношению симметрии. В зависимости от этой симметрии и от того, является ли порядок <reservedrangesplaceholder2> фильтра четным или нечетным, линейная фаза фильтр ( сохраненный в векторе length n + 1 b) имеет определенные неотъемлемые ограничения на его частотную характеристику.
| Тип линейного фазового фильтра | Порядок фильтрации | Симметрия коэффициентов | Ответ H (f), f =0 | Ответ H (f), f =1 (Nyquist) |
|---|---|---|---|---|
Тип I | Даже | четные: | Никаких ограничений | Никаких ограничений |
Тип II | Странный | четные: | Никаких ограничений | H (1) |
Тип III | Даже | нечетные: | H (0) | H (1) |
Тип IV | Странный | нечетные: | H (0) | Никаких ограничений |
Задержка фазы и групповая задержка КИХ-фильтров линейной фазы равны и постоянны по частотной полосе. Для КИХ-фильтра линейной фазы n группы групповая задержка составляет n/2, и отфильтрованный сигнал просто задерживается на n/2 временных шагов (и величина его преобразования Фурье масштабируется величиной характеристикой фильтра). Это свойство сохраняет форму волны сигналов в полосе пропускания; то есть нет фазы искажения.
Функции fir1, fir2, firls, firpm, fircls, и fircls1 все проекты типа I и II КИХ-фильтров линейной фазы по умолчанию. rcosdesign проекты только фильтров типа I. Оба firls и firpm Проект типы III и IV КИХ-фильтров линейной фазы заданные 'hilbert' или 'differentiator' флаг. cfirpm может проектировать любой тип линейного фазового фильтра, а также нелинейных фазовых фильтров.
Примечание
Поскольку частотная характеристика фильтра типа II равна нулю на частоте Найквиста («высокая» частота), fir1 не проектирует высокоскоростные и полосно-заграждающие фильтры типа II. Для нечетных n в этих случаях fir1 добавляет 1 к порядку и возвращает фильтр типа I.
Рассмотрим идеальный, или «кирпичная стенка», цифровой lowpass фильтр с частотой отключения Этот фильтр имеет амплитуду 1 на всех частотах с амплитудой менее Его импульсная характеристика последовательность h (n)
Этот фильтр не реализуем, так как его импульсная характеристика бесконечна и некаузальна. Чтобы создать импульсную характеристику с конечной продолжительностью, обрезайте ее путем применения окна. Сохраняя центральную часть импульсной характеристики в этом усечении, вы получаете КИХ-фильтр линейной фазы. Для примера, фильтр 51 длиной с частотой среза lowpass ω 0, 0,4, rad/s,
b = 0.4*sinc(0.4*(-25:25));
Примененное здесь окно представляет собой простое прямоугольное окно. По теореме Парсеваля, это фильтр длины 51, который лучше всего аппроксимирует идеальный lowpass в интегрированном смысле методом наименьших квадратов. Следующая команда отображает частотную характеристику фильтра в FVTool:
fvtool(b,1)
Обратите внимание, что ось y, показанная на рисунке ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
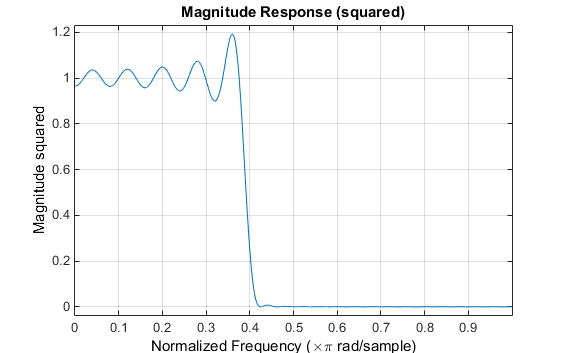
Звон и рябь происходят в ответ, особенно около ребра полосы. Этот «эффект Гиббса» не исчезает, когда длина фильтра увеличивается, но непрямоугольное окно уменьшает его величину. Умножение на окно в временной интервал вызывает свертку или сглаживание в частотный диапазон. Примените к фильтру длину 51 Окон Хэмминга и отобразите результат с помощью FVTool:
b = 0.4*sinc(0.4*(-25:25)); b = b.*hamming(51)'; fvtool(b,1)
Обратите внимание, что ось y, показанная на рисунке ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
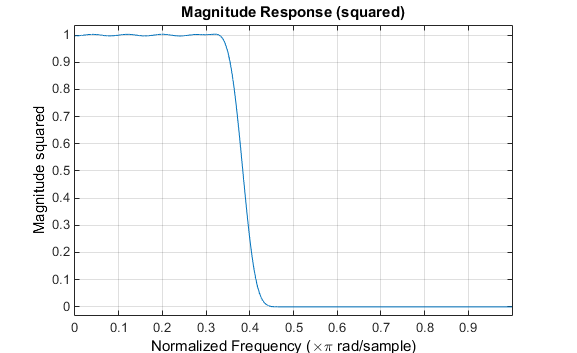
Использование окна Хэмминга значительно уменьшает звонок. Это улучшение за счет ширины перехода (оконная версия занимает больше времени, чтобы перемещаться от полосы пропускания к полосе остановки) и оптимальности (оконная версия не минимизирует интегрированную квадратичную невязку).
fir1 использует приближение методом наименьших квадратов для вычисления коэффициентов фильтра, а затем сглаживает импульсную характеристику окном. Обзор окон и их свойств см. в разделе Windows. fir1 напоминает БИХ функции создания фильтра в том, что она сформулирована для разработки фильтров в стандартных полосах строений: lowpass, bandpass, highpass и bandstop.
Операторы
n = 50; Wn = 0.4; b = fir1(n,Wn);
создать вектор-строку b содержит коэффициенты порядка n Фильтр с окном хемминга. Это lowpass, КИХ-фильтр линейной фазы с частотой среза Wn. Wn является числом от 0 до 1, где 1 соответствует частоте Найквиста, половину частоты дискретизации. (В отличие от других методов, здесь Wn соответствует точке 6 дБ.) Для highpass-фильтра просто добавьте 'high' в список параметров функции. Для полосно-пропускающего или полосно-заграждающего фильтра задайте Wn как двухэлементный вектор, содержащий частоты ребра полосы пропускания. Добавление 'stop' для строения bandstop.
b = fir1(n,Wn,window) использует окно, заданное в вектор-столбец window для проекта. Векторная window должен быть n+1 элементы длинные. Если вы не задаете окно, fir1 применяет окно Хэмминга.
Оценка порядка окна Кайзера. kaiserord функция оценивает порядок фильтра, частоту отключения и параметр окна Кайзера, необходимый для соответствия заданному набору спецификаций. Учитывая вектор ребер полосы частот и соответствующий вектор величин, а также максимально допустимую пульсацию, kaiserord возвращает соответствующие входные параметры для fir1 функция.
fir2 функция также проектирует оконные конечная импульсная характеристика, но с кусочно-линейной частотной характеристикой произвольной формы. Это контрастирует с fir1, который проектирует только фильтры в стандартных строениях lowpass, highpass, bandpass и bandstop.
Команды
n = 50; f = [0 .4 .5 1]; m = [1 1 0 0]; b = fir2(n,f,m);
возвращает вектор-строку b содержащий n+1 коэффициенты порядка n Конечная импульсная характеристика, характеристики которого совпадают с характеристиками, заданными векторами f и m. f является вектором частотных точек в диапазоне от 0 до 1, где 1 представляет частоту Найквиста. m - вектор, содержащий заданную амплитудную характеристику в точках, заданных в f. (БИХ-аналог этой функции yulewalk, который также проектирует фильтры на основе произвольных кусочно-линейных величин характеристик. Смотрите БИХ Создания фильтра для получения дополнительной информации.)
firls и firpm функции обеспечивают более общее средство определения идеального заданного фильтра, чем fir1 и fir2 функций. Эти функции проектируют трансформаторы Гильберта, дифференциаторы и другие фильтры с нечетными симметричными коэффициентами (линейная фаза типа III и типа IV). Они также позволяют включать области перехода или «не заботиться», в которых ошибка не минимизируется, и выполнять зависимое от полосы взвешивание минимизации.
The firls функция является расширением fir1 и fir2 функционирует тем, что минимизирует интеграл квадрата ошибки между заданной частотной характеристикой и фактической частотной характеристикой.
The firpm функция реализует алгоритм Паркса-Макклеллана, который использует алгоритм обмена Ремеза и теорию приближения Чебышева для разработки фильтров с оптимальными подгонками между заданной и фактической частотными характеристиками. Фильтры оптимальны в том смысле, что они минимизируют максимальную ошибку между заданной частотной характеристикой и фактической частотной характеристикой; их иногда называют минимаксными фильтрами. Фильтры, сконструированные таким образом, демонстрируют поведение равновесия по своей частотной характеристике и, следовательно, также известны как фильтры равновесия. Алгоритм конечной импульсной характеристики создания фильтра Паркса-Макклеллана, пожалуй, самый популярный и широко используемый конечная импульсная характеристика создания фильтра методологии.
Синтаксис для firls и firpm является тем же самым; единственное различие заключается в их схемах минимизации. Следующий пример показывает, как фильтры проектируются с firls и firpm отражают эти различные схемы.
Режим работы по умолчанию firls и firpm предназначен для разработки линейных фазовых фильтров типа I или типа II, в зависимости от того, является ли требуемый порядок четным или нечетным, соответственно. Пример lowpass с приблизительной амплитудой 1 от 0 до 0,4 Гц и аппроксимацией амплитуды 0 от 0,5 до 1,0 Гц является
n = 20; % Filter order f = [0 0.4 0.5 1]; % Frequency band edges a = [1 1 0 0]; % Amplitudes b = firpm(n,f,a);
От 0,4 до 0,5 Гц, firpm не выполняет минимизацию ошибок; это переходная полоса или область «не заботится». Диапазон перехода минимизирует ошибку больше в полосах, которые вы заботитесь о, за счет более медленной скорости перехода. Таким образом, эти типы фильтров имеют присущий им компромисс, подобный проекту конечной импульсной характеристики с помощью оконной обработки.
Чтобы сравнить создание фильтра методом наименьших квадратов с equiripple, используйте firls для создания аналогичного фильтра. Напечатать
bb = firls(n,f,a);
и сравните их частотные характеристики с использованием FVTool:
fvtool(b,1,bb,1)
Обратите внимание, что ось y, показанная на рисунке ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
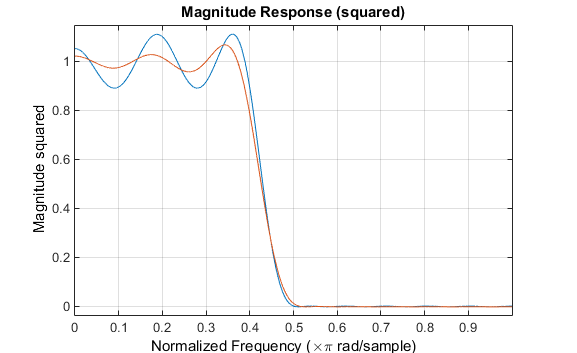
Фильтр разработан с firpm проявляет равноудаленное поведение. Также обратите внимание, что firls фильтр имеет лучшую реакцию на большую часть полосы пропускания и полосы остановки, но на ребрах полосы (f = 0.4 и f = 0.5), реакция дальше от идеала, чем firpm фильтр. Это показывает, что firpm максимальная ошибка фильтра в полосе пропускания и полосе остановки меньше, и, фактически, это наименьшая возможная для этого строения ребра полосы пропускания и длины фильтра.
Думайте о полосах частот как о линиях с короткими частотными интервалами. firpm и firls используйте эту схему, чтобы представлять любую кусочно-линейную функцию частотной характеристики с любыми полосами переходов. firls и firpm проектирование lowpass, highpass, полосно-пропускающих и полосно-заграждающих фильтров; пример полосы пропускания
f = [0 0.3 0.4 0.7 0.8 1]; % Band edges in pairs a = [0 0 1 1 0 0]; % Bandpass filter amplitude
Технически, эти f и a векторы задают пять полос:
Две полосы стопора, от 0,0 до 0,3 и от 0,8 до 1,0
Полосу пропускания от 0,4 до 0,7
Две переходные полосы, от 0,3 до 0,4 и от 0,7 до 0,8
Примеры высокоскоростных и полосно-заграждающих фильтров
f = [0 0.7 0.8 1]; % Band edges in pairs a = [0 0 1 1]; % Highpass filter amplitude f = [0 0.3 0.4 0.5 0.8 1]; % Band edges in pairs a = [1 1 0 0 1 1]; % Bandstop filter amplitude
Пример многодиапазонного полосно-пропускающего фильтра
f = [0 0.1 0.15 0.25 0.3 0.4 0.45 0.55 0.6 0.7 0.75 0.85 0.9 1]; a = [1 1 0 0 1 1 0 0 1 1 0 0 1 1];
Другой возможностью является фильтр, который имеет в качестве переходной области линию, соединяющую полосу пропускания с полосой остановки; это может помочь контролировать «беглую» амплитудную характеристику в широких областях:
f = [0 0.4 0.42 0.48 0.5 1]; a = [1 1 0.8 0.2 0 0]; % Passband, linear transition, % stopband
Оба firls и firpm позволяет вам делать больший или меньший акцент на минимизации ошибки в определенных полосах относительно других. Для этого задайте вектор веса, следующий за векторами частоты и амплитуды. Пример lowpass equiripple фильтра с 10-кратной меньшей пульсацией в полосе упора, чем ширина полосы пропускания
n = 20; % Filter order f = [0 0.4 0.5 1]; % Frequency band edges a = [1 1 0 0]; % Amplitudes w = [1 10]; % Weight vector b = firpm(n,f,a,w);
Легальный вектор веса всегда равен половине длины f и a векторы; должен быть только один вес на полосу.
При вызове с конечным 'h' или 'Hilbert' опция, firpm и firls проектировать конечная импульсная характеристика с нечетной симметрией, то есть тип III (для четного порядка) или тип IV (для нечетного порядка) линейные фазовые фильтры. Идеальный трансформатор Гильберта имеет это антисимметричное свойство и амплитуду 1 во всей частотной области значений. Попробуйте следующие приблизительные трансформаторы Гильберта и постройте график с помощью FVTool:
b = firpm(21,[0.05 1],[1 1],'h'); % Highpass Hilbert bb = firpm(20,[0.05 0.95],[1 1],'h'); % Bandpass Hilbert fvtool(b,1,bb,1)
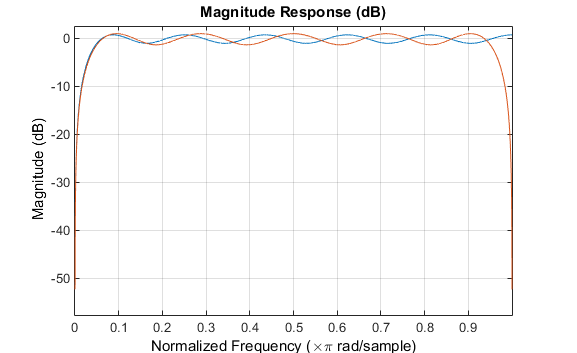
Можно найти отложенное преобразование Гильберта сигнала x путем прохождения его через эти фильтры.
fs = 1000; % Sampling frequency t = (0:1/fs:2)'; % Two second time vector x = sin(2*pi*300*t); % 300 Hz sine wave example signal xh = filter(bb,1,x); % Hilbert transform of x
Аналитический сигнал, относящийся к x является комплексным сигналом, который имеет x как его действительная часть и преобразование Гильберта x как его мнимая часть. Для этой конечной импульсной характеристики метод (альтернатива hilbert функция), вы должны задержать x на половину порядка фильтра для создания аналитического сигнала:
xd = [zeros(10,1); x(1:length(x)-10)]; % Delay 10 samples xa = xd + j*xh; % Analytic signal
Этот метод не работает непосредственно для фильтров нечетного порядка, которые требуют нецелочисленной задержки. В этом случае hilbert функция, описанная в Преобразовании Гильберта, оценивает аналитический сигнал. Кроме того, используйте resample функция для задержки сигнала на нецелое число выборок.
Дифференциация сигнала во временном интервале эквивалентна умножению преобразования Фурье сигнала на мнимую усиленную функцию. Таким образом, чтобы дифференцировать сигнал, передайте его через фильтр, у которого есть ответ H (ω) =j Аппроксимируйте идеальный дифференциатор (с задержкой), используя firpm или firls с 'd' или 'differentiator' опция:
b = firpm(21,[0 1],[0 pi],'d');
Для фильтра типа III полоса дифференцирования должен остановиться до частоты Найквиста, и вектор амплитуды должен отражать это изменение, чтобы гарантировать правильный наклон:
bb = firpm(20,[0 0.9],[0 0.9*pi],'d');
В 'd' режим, firpm взвешивает ошибку на 1/, в ненулевых полосах амплитуд, чтобы минимизировать максимальную относительную погрешность. firls взвешивает ошибку (1/2 в ненулевых полосах амплитуд в 'd' режим.
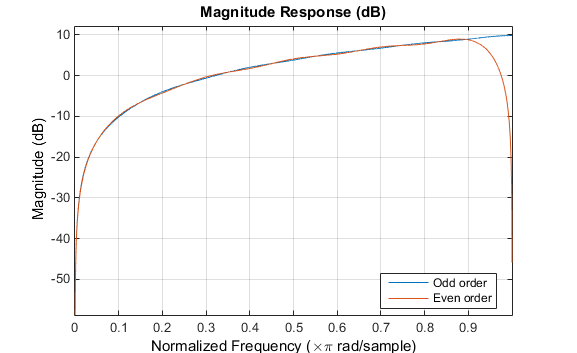
Следующие графики показывают величине отклики для дифференциаторов выше.
fvtool(b,1,bb,1) legend('Odd order','Even order','Location','best')
Функции Метода наименьших квадратов с ограничениями (CLS) конечной импульсной характеристики создания фильтра реализуют метод, который позволяет вам проектировать конечную импульсную характеристику фильтры, не определяя явно полосы перехода для величины отклика. Возможность опускать спецификацию полос полезна в нескольких ситуациях. Для примера может быть неясно, где должна появиться жестко заданная полоса перехода, если информация о шуме и сигнале появляются вместе в одной и той же частотной полосе. Точно так же может иметь смысл опускать спецификацию переходных полос, если они появляются только для управления результатами явлений Гиббса, которые появляются в отклике фильтра. Для обсуждения этого метода см. Selesnick, Lang и Burrus [2].
Вместо того, чтобы определять полосы пропускания, полосы пропускания и области перехода, метод CLS принимает частоту отключения (для случаев highpass, lowpass, bandpass или bandstop), или ребра полосы пропускания и полосы пропускания (для многодиапазонных случаев), для заданного отклика. Таким образом, метод CLS определяет области перехода неявно, а не явно.
Ключевая возможность метода CLS заключается в том, что он позволяет вам задать верхний и нижний пороги, которые содержат максимально допустимую рябь в величине отклике. Учитывая это ограничение, метод применяет метод минимизации наименьших квадратов ошибок в частотной области значений отклика фильтра, а не в конкретных полосах. Минимизация ошибок включает любые области разрыва в идеальной, «кирпичной» стенке. Дополнительным преимуществом является то, что метод позволяет вам задать произвольно маленький peaks, следующие из феномена Гиббса.
Существует две функции тулбокса, которые реализуют этот метод проекта.
Описание | Функция |
|---|---|
Ограниченные многополосные конечные импульсные характеристики с наименьшими квадратами создания фильтра | |
Ограниченные наименьшие квадратные создания фильтра для lowpass и highpass линейных фаз фильтров |
Для получения дополнительной информации о синтаксисе вызова для этих функций см. их справочные описания в Ссылка.
Самые основные функции проекта CLS, fircls1, использует этот метод для разработки lowpass и highpass конечных импульсных характеристик. В качестве примера рассмотрите разработку фильтра с импульсной характеристикой порядка 61 и частотой отключения 0,3 (нормирована). Далее задайте верхнюю и нижнюю границы, которые ограничивают процесс проекта как:
Максимальное отклонение полосы пропускания от 1 (неравномерности в полосе пропускания) 0,02.
Максимальное отклонение полосы упора от 0 (пульсация полосы упора) 0,008.
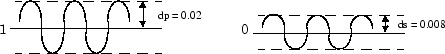
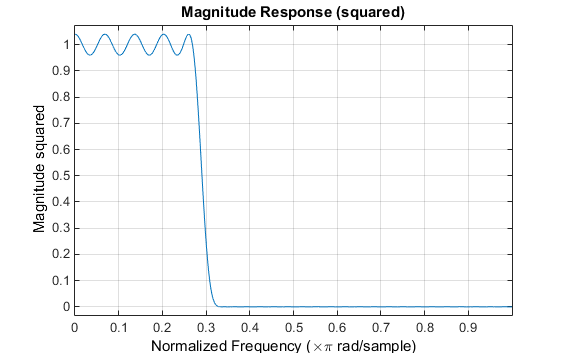
Чтобы подойти к этой задаче проекта с помощью fircls1, используйте следующие команды:
n = 61; wo = 0.3; dp = 0.02; ds = 0.008; h = fircls1(n,wo,dp,ds); fvtool(h,1)
Обратите внимание, что ось y, показанная ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
fircls использует тот же метод для разработки конечных импульсных характеристик с заданной кусочно-постоянной амплитудной характеристикой. В этом случае можно задать вектор ребер полосы и соответствующий вектор амплитуд полосы. В сложение можно задать максимальное количество пульсации для каждой полосы.
Например, предположим, что спецификации для вызова фильтра:
От 0 до 0,3 (нормировано): амплитуда 0, верхняя граница 0.005, нижняя граница -0.005
От 0,3 до 0,5: 0,5 амплитуды, верхняя граница 0,51, нижняя граница 0,49
От 0,5 до 0,7: 0 амплитуды, верхняя граница 0,03, нижняя граница -0.03
От 0,7 до 0,9: 1 амплитуды, верхняя граница 1,02, нижняя граница 0,98
От 0,9 до 1: 0 амплитуды, верхняя граница 0,05, нижняя граница -0.05
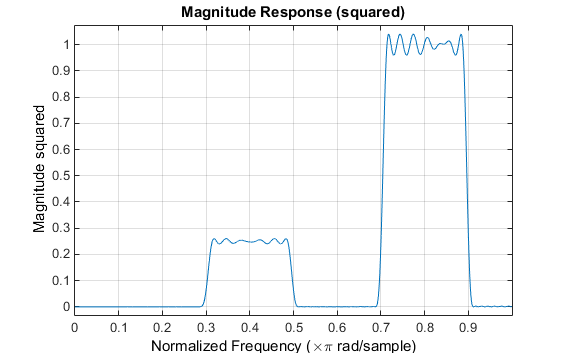
Создайте фильтр CLS с порядком импульсной характеристики 129, который удовлетворяет этим спецификациям:
n = 129; f = [0 0.3 0.5 0.7 0.9 1]; a = [0 0.5 0 1 0]; up = [0.005 0.51 0.03 1.02 0.05]; lo = [-0.005 0.49 -0.03 0.98 -0.05]; h = fircls(n,f,a,up,lo); fvtool(h,1)
Обратите внимание, что ось y, показанная ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
Взвешенное создание фильтра CLS позволяет вам проектировать lowpass или highpass конечная импульсная характеристика с относительным взвешиванием минимизации ошибок в каждой полосе. The fircls1 функция позволяет вам задать ребра полосы пропускания и полосы упора для функции взвешивания методом наименьших квадратов, а также константу k это определяет отношение веса полосы остановки к полосе пропускания.
Для примера рассмотрите спецификации, которые вызывают конечную импульсную характеристику фильтр с порядком импульсной характеристики 55 и частотой отключения 0,3 (нормирован). Также примите максимально допустимую неравномерность в полосе пропускания 0,02 и максимально допустимую пульсацию полосы упора 0,004. В сложение добавьте требования к взвешиванию:
Ширина полосы ребра для функции веса 0,28 (нормирована)
Диапазон ребра для функции веса 0,32
Минимизация весовой ошибки в 10 раз больше в полосе стопора, чем в полосе пропускания
Чтобы подойти к этому с помощью fircls1, type
n = 55; wo = 0.3; dp = 0.02; ds = 0.004; wp = 0.28; ws = 0.32; k = 10; h = fircls1(n,wo,dp,ds,wp,ws,k); fvtool(h,1)
Обратите внимание, что ось y, показанная ниже, имеет значение в квадрате. Установить его можно, щелкнув правой кнопкой мыши по подписи по осям и выбрав в меню Magnitude Squared.
cfirpm Функция создания фильтра предоставляет инструмент для разработки конечных импульсных характеристик с произвольными комплексными откликами. Он отличается от других функций создания фильтра тем, как задана частотная характеристика фильтра: он принимает имя функции, которая возвращает фильтрующую характеристику, вычисленную по сетке частот. Эта возможность делает cfirpm очень универсальный и мощный метод для создания фильтра.
Этот метод проекта может использоваться, чтобы создать нелинейные конечная импульсная характеристика, асимметричные фильтры частотной характеристики (с комплексными коэффициентами) или более симметричных фильтров с пользовательскими частотными характеристиками.
Алгоритм проекта оптимизирует ошибку Чебышева (или минимаксу), используя расширенный алгоритм Ремеза-обмена для начальной оценки. Если этот метод обмена не может получить оптимальный фильтр, алгоритм переключается на алгоритм восхождения-спуска, который берет верх, чтобы закончить сходимость к оптимальному решению.
Рассмотрим мультидиапазонный фильтр со следующими особыми характеристиками частотного диапазона.
Полоса | Амплитуда | Оптимизационное взвешивание |
|---|---|---|
[–1 –0.5] | [5 1] | 1 |
[–0.4 +0.3] | [2 2] | 10 |
[+0.4 +0.8] | [2 1] | 5 |
Линейно-фазовый многодиапазонный фильтр может быть разработан с использованием предопределенной функции частотной характеристики multiband, следующим образом:
b = cfirpm(38, [-1 -0.5 -0.4 0.3 0.4 0.8], ... {'multiband', [5 1 2 2 2 1]}, [1 10 5]);
Для конкретного случая многодиапазонного фильтра мы можем использовать сокращённое создание фильтра, подобное синтаксису для firpm:
b = cfirpm(38,[-1 -0.5 -0.4 0.3 0.4 0.8], ...
[5 1 2 2 2 1], [1 10 5]);
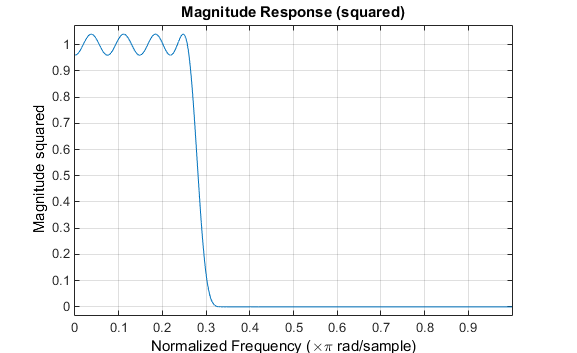
Как и в случае firpmвектор ребер полосы пропускается в cfirpm. Этот вектор задает полосы частот, над которыми выполняется оптимизация; обратите внимание, что существует две полосы переходов, от -0,5 до -0,4 и от 0,3 до 0,4.
В любом случае частотную характеристику получают и строят график с использованием линейной шкалы в FVTool:
fvtool(b,1)
Обратите внимание, что область значений данных, показанных ниже (-pi,pi).
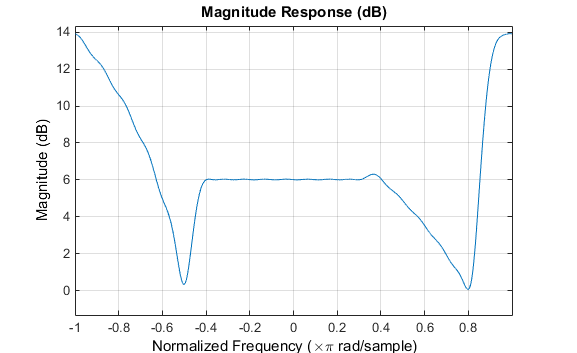
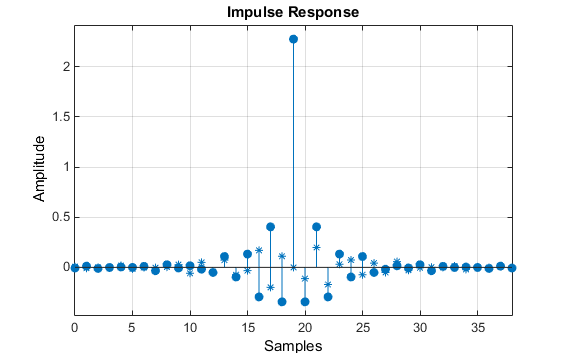
Реакция фильтра для этого многополосного фильтра сложна, что ожидается из-за асимметрии в частотный диапазон. Импульсная характеристика, которую можно выбрать на панели инструментов FVTool, показана ниже.
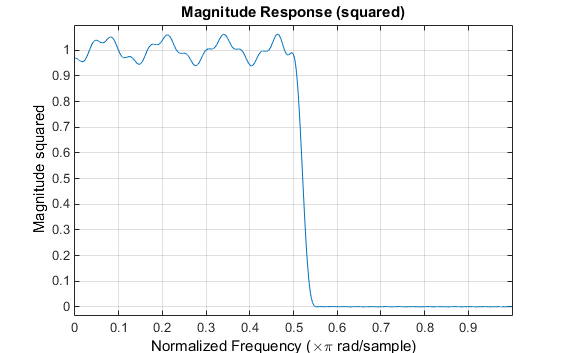
Рассмотрим проект 62-контактного lowpass с половинной отсечкой Найквиста. Если мы задаем отрицательное значение смещения к lowpass Функция создания фильтра, смещение групповой задержки для проекта значительно меньше, чем полученное для стандартной линейно-фазовой конструкции. Это создание фильтра может быть вычислена следующим образом:
b = cfirpm(61,[0 0.5 0.55 1],{'lowpass',-16});
Результат величины ответа:
fvtool(b,1)
Ось y находится в квадрате величин, который можно задать, щелкнув правой кнопкой мыши по подписи по осям и выбрав Magnitude Squared из меню.
Групповая задержка фильтра показывает, что смещение было уменьшено от N/2 на N/2-16 (т.е. от 30.5 на 14.5). Однако теперь задержка группы больше не является плоской в области полосы пропускания. Чтобы создать этот график, нажмите кнопку Group Delay Response на панели инструментов.
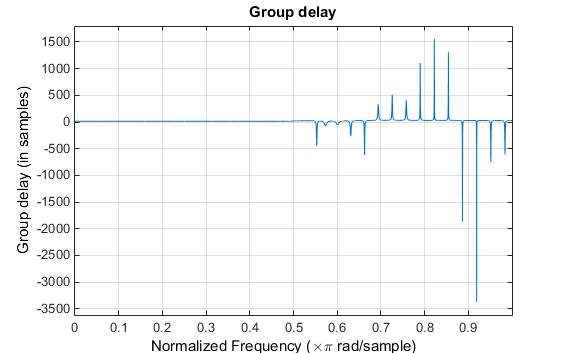
Если сравнить этот нелинейный-фазовый фильтр с линейно-фазовым фильтром, который имеет точно 14,5 выборки групповой задержки, полученный фильтр имеет порядок 2 * 14,5, или 29. Использование b = cfirpm(29,[0 0.5 0.55 1],'lowpass')Ширина полосы пропускания и пульсации ограничительной полосы намного больше для порядка 29 фильтра. Эти сравнения могут помочь вам решить, какой фильтр более подходит для определенного приложения.