Основное преимущество БИХ по сравнению с конечная импульсная характеристика заключается в том, что они обычно отвечают заданному набору спецификаций с гораздо более низким порядком фильтра, чем соответствующий конечная импульсная характеристика. Несмотря на то, что БИХ имеют нелинейную фазу, обработка данных в MATLAB® программное обеспечение обычно выполняется «в автономном режиме», то есть вся последовательность данных доступна перед фильтрацией. Это позволяет использовать некаузальный, нулевой подход к фильтрации фазы (через filtfilt function), что устраняет нелинейную фазу искажение БИХ фильтра.
Классические БИХ, Butterworth, Chebyshev Types I и II, эллиптические, и Бессель, все по-разному аппроксимируют идеальный фильтр «кирпичная стенка».
Этот тулбокс обеспечивает функции для создания всех этих типов классического БИХ как в аналоговом, так и в цифровом областях (кроме Бесселя, для которого поддерживается только аналоговый случай), и в lowpass, highpass, полосно-пропускающей и полосно-заграждающей строениях. Для большинства типов фильтров можно также найти самый низкий порядок фильтра, который соответствует заданной спецификации фильтра с точки зрения полосы пропускания и затухания в полосе задерживания и ширины (ширин) перехода.
Функция прямого создания фильтра yulewalk находит фильтр с величиной характеристикой, аппроксимирующей заданную функцию частотной характеристики. Это один из способов создать многодиапазонный полосно-пропускающий фильтр.
Можно также использовать параметрическое моделирование или функции системы идентификации для разработки БИХ. Эти функции обсуждаются в Parametric Modeling.
Обобщенная функция проекта Butterworth maxflat обсуждается в разделе «Общая разработка фильтра Баттерворта».
В следующей таблице представлены различные методы фильтрации в тулбоксе и перечислены функции, доступные для реализации этих методов.
Методы фильтров тулбокса и доступные функции
| Метод фильтра | Описание | Функции filter |
|---|---|---|
Аналоговое прототипирование | Используя полюса и нули классического lowpass прототипа фильтра в непрерывной (Laplace) области, получите цифровой фильтр через преобразование частоты и дискретизацию фильтра. | Полные функции проекта: besself, butter, cheby1, cheby2, ellipФункции оценки порядка: buttord, cheb1ord, cheb2ord, ellipordФункции Lowpass аналогового прототипа: besselap, buttap, cheb1ap, cheb2ap, ellipapФункции частотного преобразования: lp2bp, lp2bs, lp2hp, lp2lpФункции дискретизации фильтра: bilinear, impinvar |
Прямой проект | Проектируйте цифровой фильтр непосредственно в дискретной временной области путем аппроксимации кусочно-линейной амплитудной характеристики. | |
Обобщённый проект Butterworth | Проектируйте lowpass фильтры Баттерворта с большим количеством нулей, чем полюса. | |
Параметрическое моделирование | Найдите цифровой фильтр, который аппроксимирует предписанный временной или частотный диапазон ответ. (Подробную коллекцию параметрических инструментов моделирования см. в документации System Identification Toolbox™.) | Функции моделирования во временной области: lpc, prony, stmcbФункции моделирования частотного диапазона: invfreqs, invfreqz |
Основной метод создания цифровых фильтров БИХ, который предоставляет этот тулбокс, основан на преобразовании классических lowpass аналоговых фильтров в их цифровые эквиваленты. В следующих разделах описывается, как проектировать фильтры и результирующие характеристики поддерживаемых типов фильтров. Для получения подробной информации о процессе разработки фильтра см. Специальные темы в БИХ Filter Design.
Можно легко создать фильтр любого порядка с lowpass, highpass, bandpass или bandstop строения с помощью функций создания фильтра.
Создания фильтра
Тип фильтра | Проект |
|---|---|
Бессель (только аналоговый) |
|
Баттерворт |
|
Чебышевский тип I |
|
Чебышёвский тип II |
|
Овальный |
|
По умолчанию каждая из этих функций возвращает lowpass; вам нужно задать только частоту отключения, которую вы хотите, Wn, в нормированных модулях такой, что частота Найквиста составляет 1 Гц). Для высокоскоростного фильтра добавьте 'high' в список параметров функции. Для полосно-пропускающего или полосно-заграждающего фильтра задайте Wn как двухэлементный вектор, содержащий частоты ребра полосы пропускания. Добавление 'stop' для строения bandstop.
Вот некоторые примеры цифровых фильтров:
[b,a] = butter(5,0.4); % Lowpass Butterworth [b,a] = cheby1(4,1,[0.4 0.7]); % Bandpass Chebyshev Type I [b,a] = cheby2(6,60,0.8,'high'); % Highpass Chebyshev Type II [b,a] = ellip(3,1,60,[0.4 0.7],'stop'); % Bandstop elliptic
Чтобы спроектировать аналоговый фильтр, возможно, для симуляции, используйте конечный 's' и укажите частоты отключения в рад/с:
[b,a] = butter(5,0.4,'s'); % Analog Butterworth filter
Все функции создания фильтра возвращают фильтр в передаточной функции, нули , полюса и усиления или представление линейной системной модели пространства состояний, в зависимости от того, сколько выходных аргументов присутствует. В целом следует избегать использования формы передаточной функции, поскольку могут возникнуть числовые проблемы, вызванные ошибками округления. Вместо этого используйте форму с нулями , полюса и усиления, которую можно преобразовать в форму с секцией второго порядка (SOS), используя zp2sos а затем используйте форму SOS для анализа или реализации вашего фильтра.
Примечание
Весь классический lowpass БИХ плохо обусловлены для чрезвычайно низких частот отключения. Поэтому вместо разработки lowpass БИХ с очень узкой полосой пропускания может быть лучше спроектировать более широкую полосу пропускания и децимировать входной сигнал.
Этот тулбокс обеспечивает функции выбора порядка, которые вычисляют минимальный порядок фильтра, соответствующий заданному набору требований.
Тип фильтра | Функция оценки порядка |
|---|---|
Баттерворт |
|
Чебышевский тип I |
|
Чебышёвский тип II |
|
Овальный |
|
Они полезны в сочетании с функциями создания фильтра. Предположим, вам нужен полосно-пропускающий фильтр с полосой пропускания от 1000 до 2000 Гц, полосами остановки, начинающимися на 500 Гц от обеих сторон, частотой дискретизации 10 кГц, самое большее 1 дБ неравномерности в полосе пропускания и по крайней мере 60 дБ затухания в полосе задерживания. Вы можете соответствовать этим спецификациям при помощи butter функционировать следующим образом.
[n,Wn] = buttord([1000 2000]/5000,[500 2500]/5000,1,60) [b,a] = butter(n,Wn);
n =
12
Wn =
0.1951 0.4080Эллиптический фильтр, который соответствует тем же требованиям, дается
[n,Wn] = ellipord([1000 2000]/5000,[500 2500]/5000,1,60) [b,a] = ellip(n,1,60,Wn);
n =
5
Wn =
0.2000 0.4000Эти функции также работают с другими стандартными строениями полосы, а также с аналоговыми фильтрами.
Тулбокс предоставляет пять различных типов классического БИХ, каждый из которых в некотором роде оптимален. В этом разделе показана основная форма аналогового прототипа для каждого и обобщены основные характеристики.
Фильтр Баттерворта предоставляет лучшее серийное приближение Тейлора идеальному ответу фильтра lowpass на аналоговых частотах Ω = 0 и Ω = ∞; для любого порядка <reservedrangesplaceholder1> согласовалась величина, ответ имеет 2 N - 1 нулевая производная в этих местоположениях ( максимально плоский в Ω = 0 и Ω = ∞). Реакция монотонна в целом, плавно уменьшается с В = 0 до В = ∞. при в, = 1.
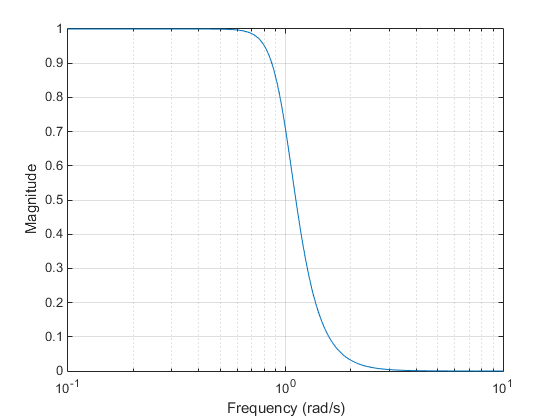
Фильтр Чебышевский Тип 1 минимизирует абсолютное различие между идеальной и фактической частотной характеристикой по всей полосе пропускания путем включения равной пульсации Rp дБ в полосе пропускания. Реакция Stopband максимально плоская. Переход от полосы пропускания к полосе остановки более быстрый, чем для фильтра Баттерворта. при в, = 1.

Фильтр Чебышёва типа II минимизирует абсолютное различие между идеальной и фактической частотной характеристикой во всем диапазоне остановок путем включения равной пульсации Rs дБ в полосе пробок. Реакция полосы пропускания максимально плоская.
Диапазон остановки не приближается к нулю так быстро, как фильтр типа I (и не приближается к нулю вообще для четных n порядка фильтра). Однако отсутствие пульсации в полосе пропускания часто является важным преимуществом. при в, = 1.
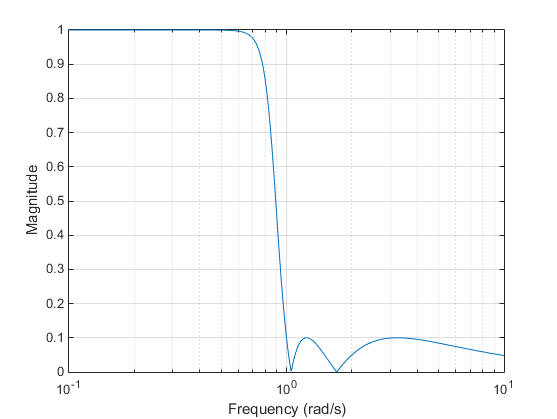
Эллиптические фильтры являются равноудаленными как в полосе пропускания, так и в полосе упора. Они обычно отвечают требованиям к фильтру с самым низким порядком для любого поддерживаемого типа фильтра. Учитывая порядок фильтра , n неравномерность в полосе пропускания Rp в децибелах и полосе упора Rs в децибелах эллиптические фильтры минимизируют ширину перехода. при в, = 1.
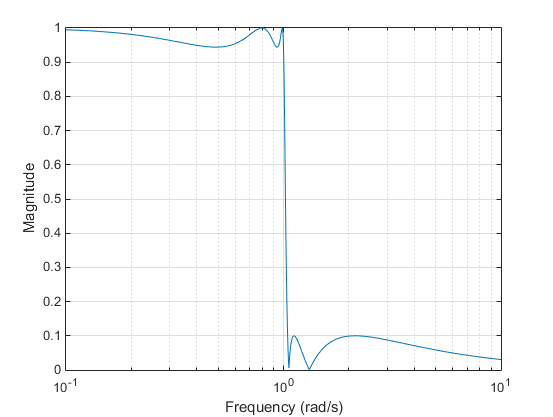
Аналоговые lowpass Бесселя имеют максимально плоскую групповую задержку на нулевой частоте и сохраняют почти постоянную групповую задержку по всей полосе пропускания. Поэтому отфильтрованные сигналы поддерживают свои волны в области значений частот полосы пропускания. Когда аналоговый lowpass Бесселя преобразуется в цифровой посредством отображения частоты, он больше не имеет этого максимально плоского свойства. Signal Processing Toolbox™ поддерживает только аналоговый случай для полной функции создания фильтра Бесселя.
Фильтры Бесселя обычно требуют более высокого порядка фильтра, чем другие фильтры, для удовлетворительного затухания в полосе задерживания. при И = 1 и уменьшается как порядок фильтра n увеличений.
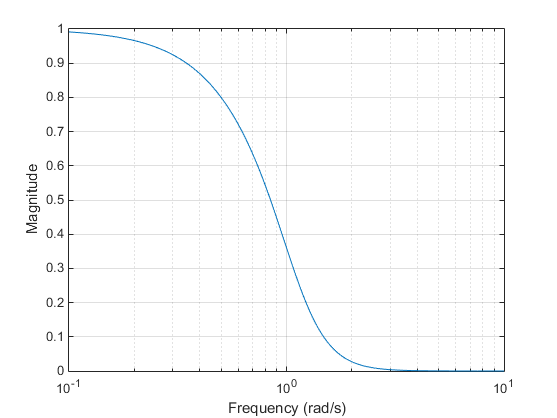
Примечание
Lowpass, показанные выше, были созданы с функциями аналогового прототипа besselap, buttap, cheb1ap, cheb2ap, и ellipap. Эти функции находят нули, полюсы и усиление nаналоговый фильтр I порядка соответствующего типа с частотой отключения 1 рад/с. Полные создания фильтра функции (besself, butter, cheby1, cheby2, и ellip) вызвать функции прототипирования как первый шаг в процессе проекта. Для получения дополнительной информации см. Специальные темы в БИХ Создания фильтра.
Чтобы создать похожие графики, используйте n = 5 и, при необходимости Rp = 0.5 и Rs = 20. Для примера, чтобы создать эллиптический график фильтра:
[z,p,k] = ellipap(5,0.5,20); w = logspace(-1,1,1000); h = freqs(k*poly(z),poly(p),w); semilogx(w,abs(h)), grid xlabel('Frequency (rad/s)') ylabel('Magnitude')
Этот тулбокс использует термин direct для описания методов для проекта БИХ, которые находят фильтр на основе спецификаций в дискретной области. В отличие от метода аналогового прототипирования, методы прямого проекта не ограничены стандартными строениями lowpass, highpass, bandpass или bandstop. Скорее эти функции проектируют фильтры с произвольной, возможно, многополосной, частотной характеристикой. В этом разделе рассматриваются yulewalk функция, которая предназначена специально для создания фильтра; Параметрическое моделирование обсуждает другие методы, которые также могут рассматриваться как прямые, такие как метод Прони, Линейное предсказание, метод Штейглица-Макбрайда и обратные частотные проекты.
yulewalk функция проектирует рекурсивные цифровые фильтры БИХ путем установки заданной частотной характеристики. yulewalkимя фильтра отражает его метод нахождения коэффициентов знаменателя: он находит обратное БПФ идеальной заданной амплитудно-квадратной характеристики и решает модифицированные уравнения Юла-Уокера с помощью получившихся выборок автокорреляционной функции. Оператор
[b,a] = yulewalk(n,f,m)
возвращает векторы-строки b и a содержащий n+1 числитель и коэффициенты знаменателя nБИХ I порядка, характеристики которого аппроксимируют характеристики, заданные в векторах f и m. f является вектором частотных точек в диапазоне от 0 до 1, где 1 представляет частоту Найквиста. m - вектор, содержащий заданную амплитудную характеристику в точках в f. f и m может описывать любую кусочно-линейную характеристику величины формы, включая многодиапазонную характеристику. Конечная импульсная характеристика аналог этой функции fir2, который также проектирует фильтр на основе произвольной кусочно-линейной величины характеристики. Для получения дополнительной информации см. Конечную импульсную характеристику Создания фильтра.
Обратите внимание, что yulewalk не принимает информацию фазы, и не делают операторов об оптимальности полученного фильтра.
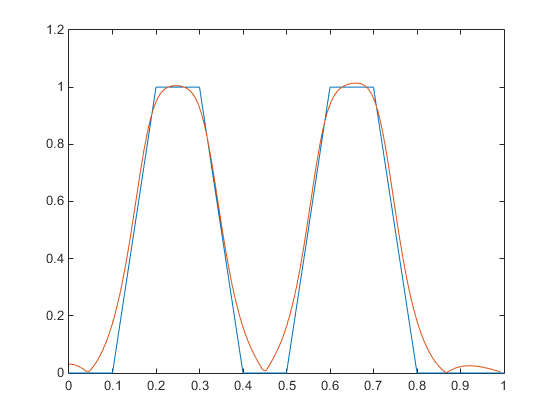
Проектируйте многодиапазонный фильтр с yulewalk и постройте график заданной и фактической частотной характеристики:
m = [0 0 1 1 0 0 1 1 0 0]; f = [0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 1]; [b,a] = yulewalk(10,f,m); [h,w] = freqz(b,a,128) plot(f,m,w/pi,abs(h))
Функция тулбокса maxflat позволяет вам проектировать обобщенные фильтры Баттерворта, то есть фильтры Баттерворта с различными числами нулей и полюсов. Это желательно в некоторых реализациях, где полюсы дороже вычислительных, чем нули. maxflat так же, как и butter функция, кроме того, что она может задавать два порядка (один для числителя и один для знаменателя) вместо одного. Эти фильтры максимально плоские. Это означает, что полученный фильтр оптимален для любых порядков числителя и знаменателя с максимальным количеством производных в 0 и частотой Найквиста ω = π обоих набором 0.
Для примера, когда два порядков одинаковы, maxflat то же, что и butter:
[b,a] = maxflat(3,3,0.25)
b =
0.0317 0.0951 0.0951 0.0317
a =
1.0000 -1.4590 0.9104 -0.1978[b,a] = butter(3,0.25)
b =
0.0317 0.0951 0.0951 0.0317
a =
1.0000 -1.4590 0.9104 -0.1978Однако, maxflat более универсален, потому что позволяет проектировать фильтр с большим количеством нулей, чем полюса:
[b,a] = maxflat(3,1,0.25)
b =
0.0950 0.2849 0.2849 0.0950
a =
1.0000 -0.2402Третий вход в maxflat - полустепень частота, частота от 0 до 1 с величиной характеристикой .
Можно также проектировать линейные фильтры фазы, которые имеют максимально плоское свойство, используя 'sym' опция:
maxflat(4,'sym',0.3)ans =
0.0331 0.2500 0.4337 0.2500 0.0331Для получения полной информации о maxflat алгоритм, см. Селесник и Беррус [2].