Концепции Алгебраических циклов

В Simulink^® модель, algebraic loop происходит, когда цикл сигнала существует только с прямыми блоками сквозного соединения в цикле. Direct feedthrough означает, что Simulink нужно значение входного сигнала блока, чтобы вычислить его выход на текущем временном шаге. Такой цикл сигнала создает круговую зависимость выходов и входов блоков в том же временном шаге. Это приводит к алгебраическому уравнению, которое нуждается в решении в каждом временном шаге, добавляя вычислительные затраты к симуляции.

Некоторые примеры блоков с прямыми исходными входами:

Math Function
Gain
Product
State-Space, когда D-матричный коэффициент ненулевой
Sum
Transfer Fcn, когда числитель и знаменатель имеют одинаковый порядок
Zero-Pole, когда блок имеет столько нулей, сколько полюсов

Ненаправленные сквозные соединения поддерживают переменную State. Два примера являются Integrator и Unit Delay.

Совет

Чтобы определить, имеет ли блок прямое сквозное соединение, прочитайте Characteristics раздел страницы с описанием блока.

Рисунок показывает пример алгебраического цикла. Sum блок - алгебраический переменный <reservedrangesplaceholder9> <reservedrangesplaceholder8>_{, который} вынужден равняться первому входу u минус <reservedrangesplaceholder6> <reservedrangesplaceholder5> (например, <reservedrangesplaceholder4> <reservedrangesplaceholder3> = u - <reservedrangesplaceholder1> <reservedrangesplaceholder0>).

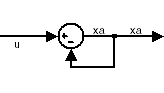
Решение этого простого цикла x a = u/2.

Математическая интерпретация

Simulink содержит набор числовых решателей для симуляции ordinary differential equations (ODEs), которые являются системами уравнений, которые можно записать как

$\dot{x} = f (x, t),$

где x - вектор состояния, а t - независимая временная переменная.

Некоторые системы уравнений содержат дополнительные ограничения, которые включают независимую переменную и вектор состояния, но не производную вектора состояния. Такие системы называются differential algebraic equations (DAEs),

Термин algebraic относится к уравнениям, которые не включают никаких производных. Вы можете выразить ДАУ, которые возникают в инженерии в полуявной форме

$\begin{array}{l} \dot{x} = f (x, x_{a}, t) \\ 0 = g (x, x_{a}, t), \end{array}$

где:

f и g могут быть векторными функциями.
Первое уравнение является дифференциальным уравнением.
Второе уравнение является алгебраическим уравнением.
Вектор дифференциальных переменных x.
Вектор алгебраических переменных равен x a.

В моделях Simulink алгебраические циклы являются алгебраическими ограничениями. Модели с алгебраическими циклами задают систему дифференциальных алгебраических уравнений. Simulink решает алгебраические уравнения (алгебраический цикл) численно для x a на каждом шаге решателя ОДУ.

Модель на рисунке эквивалентна этой системе уравнений в полуявной форме:

$\begin{array}{l} \dot{x} = f (x, x_{a}, t) = x_{a} \\ 0 = g (x, x_{a}, t) = - x + u - 2 x_{a} . \end{array}$

На каждом шаге решателя ОДУ решатель алгебраического цикла должен решить алгебраическое ограничение для x a перед вычислением производной $\dot{x}$ .

Физическая интерпретация

Алгебраические ограничения:

Происходят при моделировании физических систем, часто из-за законов сохранения, таких как сохранение массы и энергии
Происходит, когда вы выбираете конкретную систему координат для модели
Помогают наложить проект ограничения на отклики системы в динамической системе

Используйте Simscape™ для моделирования систем, которые охватывают механические, электрические, гидравлические и другие физические области как физические сети. Simscape создает ДАУ, которые характеризуют поведение модели. Программа интегрирует эти уравнения с остальной частью модели, а затем решает ДАУ непосредственно. Simulink решает переменные для компонентов в различных физических доменах одновременно, избегая проблем с алгебраическими циклами.

Искусственные Алгебраические циклы

Искусственный алгебраический цикл возникает, когда атомарная подсистема или блок Model заставляет Simulink обнаружить алгебраический цикл, даже если содержимое подсистемы не содержит прямого сквозного соединения от входа к выходу. Когда вы создаете атомарную подсистему, все блоки Inport являются прямым сквозным соединением, что приводит к алгебраическому циклу.

Начните с включенной модели, которая представляет собой простое пропорциональное управление объектом, описанное

$G(s) = \frac{1}{s^2+2s+1}$

который может быть переписан в форме пространство состояний как

$
\dot{x} = \left[
 \begin{array}{cc}
 -2 & -1 \\
1 & 0
 \end{array}
 \right]
+ \left(
\begin{array}{c}
0\\1
\end{array}
\right)
$

$
y = \left[\begin{array}{cc}0&1\end{array}\right]
$

Система не имеет ни алгебраических переменных, ни прямого сквозного соединения и не содержит алгебраического цикла.

Измените модель так, как описано в следующих шагах:

Заключайте блоки Controller и Plant в подсистему.
В диалоговом окне подсистемы выберите Treat as atomic unit, чтобы сделать подсистему атомарной.
На панели Diagnostics Параметров конфигурации модели установите параметр Алгебраический цикл на error.

При симуляции этой модели возникает алгебраический цикл, потому что подсистема является прямым сквозным соединением, хотя путь внутри атомарной подсистемы не является прямым сквозным соединением. Симуляция останавливается с алгебраической ошибкой цикла.

Как работает Алгебраический Решатель Цикла

Когда модель содержит алгебраический цикл, Simulink использует нелинейный решатель на каждом временном шаге, чтобы решить алгебраический цикл. Решатель выполняет итерации, чтобы определить решение алгебраического ограничения, если оно существует. В результате модели с алгебраическими циклами могут работать медленнее, чем модели без алгебраических циклов.

Simulink использует алгоритм резкого искривления области доверия, чтобы решить алгебраические циклы. Используемый допуск меньше, чем решатель ODE Reltol и Abstol. Это связано с тем, что Simulink использует «явный метод ОДУ», чтобы решить Индекс дифференциальных алгебраических уравнений (ДАУ) -1.

Для работы алгебраического решателя цикла,

Должен быть один блок, где решатель цикла может сломать цикл и попытаться решить цикл.
Модель должна иметь реальные сигналы double.
Базовое алгебраическое ограничение должно быть сглаженной функцией

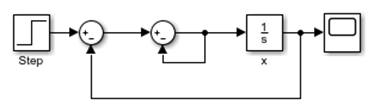
Например, предположим, что ваша модель имеет блок Sum с двумя входами - одна аддитивная, другая вычитающая. Если вы подаете выход блока Sum на один из входов, вы создадите алгебраический цикл, где все блоки включают прямое сквозное соединение.

Блок Sum не может вычислить выход, не зная входов. Simulink обнаруживает алгебраический цикл, и решатель алгебраического цикла решает цикл с помощью итерационного цикла. В примере блока Sum программное обеспечение вычисляет правильный результат следующим образом:

<reservedrangesplaceholder4> <reservedrangesplaceholder3> (<reservedrangesplaceholder2>) = u (<reservedrangesplaceholder0>) / 2.

(1)

Алгебраический петельный решатель использует основанный на градиенте метод поиска, который требует непрерывных первых производных алгебраического ограничения, которые соответствуют алгебраическому циклу. В результате, если алгебраический цикл содержит разрывы, решатель алгебраического цикла может потерпеть неудачу.

Для получения дополнительной информации смотрите Решение Индекса -1 ДАУ в MATLAB и Simulink ^[1]

Алгоритмы доверительной области и линейного поиска в решателе Алгебраического цикла

Решатель алгебраического цикла Simulink использует один из двух алгоритмов, чтобы решить алгебраические циклы:

Доверительная область
Поиск по строке

По умолчанию Simulink выбирает лучший алгебраический решатель цикла и может переключаться между этими двумя методами во время симуляции. Чтобы явным образом включить автоматический выбор решателя алгебраического цикла для вашей модели, в MATLAB^® в командной строке введите:

set_param(model_name, 'AlgebraicLoopSolver','Auto');

Чтобы переключиться на алгоритм доверительной области, в командной строке MATLAB введите:

set_param(model_name, 'AlgebraicLoopSolver', 'TrustRegion');

Если решатель алгебраического цикла не может решить алгебраический цикл с помощью алгоритма доверительной области, попробуйте симулировать модель с помощью алгоритма линейного поиска.

Чтобы переключиться на алгоритм линейного поиска, в командной строке MATLAB введите:

set_param(model_name, 'AlgebraicLoopSolver', 'LineSearch');

Для получения дополнительной информации смотрите:

Шемпин и Рейхельта nleqn.m
Программа Фортран HYBRD1 в Руководство пользователя по MINPACK-1 ^[2]
«A Фортран стандартной подпрограммы Пауэлла для решения систем в нелинейных уравнениях», в численных методах для нелинейных алгебраических уравнений^[3]
Методы доверительной области для нелинейной минимизации (Optimization Toolbox).
Поиск по линии (Optimization Toolbox).

Ограничения решателя Алгебраического Цикла

Алгебраическое решение цикла является итеративным процессом. Решатель алгебраического цикла Simulink успешен только, если алгебраический цикл сходится к определенному ответу. Когда цикл не сходится или сходится слишком медленно, симуляция выходит с ошибкой.

Алгебраический решатель цикла не может решить алгебраические циклы, которые содержат любое из следующего:

Блоки с дискретными выходами
Блоки с неразрешенными или комплексными выходами
Неоднородности
Stateflow^® чарты

Последствия алгебраических циклов в модели

Если ваша модель содержит алгебраический цикл:

Вы не можете сгенерировать код для модели.
Решатель алгебраического цикла Simulink, возможно, не сможет решить алгебраический цикл.
В то время как Simulink пытается решить алгебраический цикл, симуляция может выполняться медленно.
Для большинства моделей алгебраический решатель цикла является вычислительно дорогим для первого временного шага. Simulink быстро решает последующие временные шаги, потому что хорошая начальная точка для x a доступна с предыдущего временного шага.

См. также

Алгебраическое ограничение | Сравнение решателей | Пространство состояний дескриптора | Обнаружение пересечения нулем

Документация