Модели линейной регрессии описывают линейную зависимость между откликом и одним или несколькими прогнозирующими терминами. Однако много раз существует нелинейная связь. Нелинейная регрессия описывает общие нелинейные модели. Специальный класс нелинейных моделей, называемый обобщенными линейными моделями, использует методы Linear.
Напомним, линейные модели имеют такие характеристики:
В каждом множестве значений для предикторов ответ имеет нормальное распределение со средним μ.
Вектор b коэффициентов задает линейную комбинацию X b из X предикторов.
Модель является μ = X b.
В обобщенных линейных моделях эти характеристики обобщаются следующим образом:
В каждом множестве значений для предикторов ответ имеет распределение, которое может быть нормальным, биномиальным, Пуассоном, гамма или обратным Гауссовым, с параметрами, включающими среднюю μ.
Вектор b коэффициентов задает линейную комбинацию X b из X предикторов.
<reservedrangesplaceholder5> <reservedrangesplaceholder4> определяет модель как f (<reservedrangesplaceholder2>) = <reservedrangesplaceholder1> <reservedrangesplaceholder0>.
Чтобы начать подгонку регрессии, поместите свои данные в форму, которую ожидают функции аппроксимации. Все методы регрессии начинаются с входных данных в массиве X и данные отклика в отдельном векторе y, или входные данные в таблице или массиве набора данных tbl и данные отклика в виде столбца в tbl. Каждая строка входных данных представляет одно наблюдение. Каждый столбец представляет один предиктор (переменную).
Для таблицы или массива набора данных tbl, укажите переменную отклика с 'ResponseVar' Пара "имя-значение":
mdl = fitglm(tbl,'ResponseVar','BloodPressure');
Переменная отклика по умолчанию является последним столбцом.
Можно использовать числовые предикторы categorical. Категориальный предиктор является таким, который принимает значения из фиксированного набора возможностей.
Для числового X массива, укажите категориальные предикторы, использующие 'Categorical' Пара "имя-значение". Для примера указать, что предикторы 2 и 3 из шести категоричны:
mdl = fitglm(X,y,'Categorical',[2,3]); % or equivalently mdl = fitglm(X,y,'Categorical',logical([0 1 1 0 0 0]));
Для таблицы или массива набора данных tblфункции аппроксимации предполагают, что эти типы данных категориальны:
Логический вектор
Категориальный вектор
Символьный массив
Строковые массивы
Если вы хотите указать, что числовой предиктор категориален, используйте 'Categorical' Пара "имя-значение".
Представьте отсутствующие числовые данные как NaN. Представление отсутствующих данных для других типов данных смотрите в Отсутствующие значения группы.
Для 'binomial' модель с матрицей данных X, ответ y могут быть:
Двухкомпонентный вектор-столбец - каждая запись представляет успех (1) или отказ (0).
Двухколоночная матрица целых чисел - первый столбец - количество успехов в каждом наблюдении, второй столбец - количество испытаний в этом наблюдении.
Для 'binomial' модель с таблицей или набором данных tbl:
Используйте ResponseVar Пара "имя-значение", чтобы задать столбец tbl это дает количество успехов в каждом наблюдении.
Используйте BinomialSize Пара "имя-значение", чтобы задать столбец tbl это дает количество испытаний в каждом наблюдении.
Например, чтобы создать массив набора данных из Excel® электронная таблица:
ds = dataset('XLSFile','hospital.xls',... 'ReadObsNames',true);
Чтобы создать массив набора данных из переменных рабочей области:
load carsmall
ds = dataset(MPG,Weight);
ds.Year = ordinal(Model_Year);Чтобы создать таблицу из переменных рабочей области:
load carsmall
tbl = table(MPG,Weight);
tbl.Year = ordinal(Model_Year);Например, чтобы создать числовые массивы из переменных рабочей области:
load carsmall
X = [Weight Horsepower Cylinders Model_Year];
y = MPG;Чтобы создать числовые массивы из электронной таблицы Excel:
[X, Xnames] = xlsread('hospital.xls'); y = X(:,4); % response y is systolic pressure X(:,4) = []; % remove y from the X matrix
Заметьте, что нечисловые значения, такие как sex, не появляться в X.
Часто ваши данные предполагают тип распределения обобщенной линейной модели.
| Тип данных отклика | Предлагаемый тип распределения модели |
|---|---|
| Любое действительное число | 'normal' |
| Любое положительное число | 'gamma' или 'inverse gaussian' |
| Любое неотрицательное целое число | 'poisson' |
Целое число от 0 до n, где n является фиксированным положительным значением | 'binomial' |
Установите тип распределения модели с помощью Distribution Пара "имя-значение". После выбора типа модели выберите функцию ссылки, чтобы сопоставить среднее µ и Xb линейного предиктора.
| Значение | Описание |
|---|---|
'comploglog' | журнал (-журнал ((1 - µ))) = Xb |
| µ = Xb |
| журнал (µ) = Xb |
| журнал (µ/( 1 - µ)) = Xb |
| журнал (-журнал (µ)) = Xb |
'probit' | Φ–1(µ) = Xb, где И является нормальной (Гауссовой) совокупной функцией распределения |
'reciprocal', по умолчанию для распределительного 'gamma' | µ–1 = Xb |
| µp = Xb |
Массив ячеек вида | Пользовательская функция ссылки (см. «Пользовательская функция ссылки») |
Функции ссылки nondefault в основном полезны для биномиальных моделей. Эти функции ссылки nondefault 'comploglog', 'loglog', и 'probit'.
Функция ссылки определяет отношения f (<reservedrangesplaceholder6>) = Xb между средним ответом µ и линейной комбинацией Xb = X * b предсказателей. Можно выбрать одну из встроенных функций ссылки или определить свою собственную, задав функцию ссылки FL, его производная FD, и его обратное FI:
Функция ссылки FL вычисляет f (µ).
Производная функции ссылки FD вычисляет df (µ )/ dµ.
Обратная функция FI вычисляет g (Xb) = µ.
Вы можете задать пользовательскую функцию ссылки любым из двух эквивалентных способов. Каждый способ содержит указатели на функцию, которые принимают один массив значений, представляющих µ или Xb, и возвращают массив того же размера. Указатели на функцию находятся либо в массиве ячеек, либо в структуре:
Массив ячеек вида {FL FD FI}, содержащий три указателя на функцию, созданные с помощью @, которые определяют ссылку (FL), производная ссылка (FD), и обратной ссылки связи (FI).
Структурные s@:
s.Link
s.Derivative
s.Inverse
Для примера подбирать модель используя 'probit' функция ссылки:
x = [2100 2300 2500 2700 2900 ... 3100 3300 3500 3700 3900 4100 4300]'; n = [48 42 31 34 31 21 23 23 21 16 17 21]'; y = [1 2 0 3 8 8 14 17 19 15 17 21]'; g = fitglm(x,[y n],... 'linear','distr','binomial','link','probit')
g =
Generalized Linear regression model:
probit(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Вы можете выполнить ту же подгонку с помощью пользовательской функции link, которая выполняет аналогично 'probit' функция ссылки:
s = {@norminv,@(x)1./normpdf(norminv(x)),@normcdf};
g = fitglm(x,[y n],...
'linear','distr','binomial','link',s)g =
Generalized Linear regression model:
link(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Две модели одинаковы.
Эквивалентно можно писать s как структура вместо cell-массива указателей на функцию:
s.Link = @norminv; s.Derivative = @(x) 1./normpdf(norminv(x)); s.Inverse = @normcdf; g = fitglm(x,[y n],... 'linear','distr','binomial','link',s)
g =
Generalized Linear regression model:
link(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -7.3628 0.66815 -11.02 3.0701e-28
x1 0.0023039 0.00021352 10.79 3.8274e-27
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 241, p-value = 2.25e-54Существует два способа создать подобранную модель.
Использовать fitglm когда у вас есть хорошее представление о вашей обобщенной линейной модели, или когда вы хотите настроить свою модель позже, чтобы включить или исключить определенные условия.
Использовать stepwiseglm когда вы хотите подогнать свою модель используя ступенчатую регрессию. stepwiseglm начинается с одной модели, такой как константа, и складывает или вычитает условия по одному, выбирая оптимальный термин каждый раз жадным способом, пока он не может улучшиться дальше. Используйте пошаговую подгонку, чтобы найти хорошую модель, которая имеет только релевантные условия.
Результат зависит от стартовой модели. Обычно, начиная с постоянной модели, приводит к небольшой модели. Начиная с большего количества членов может привести к более сложной модели, но той, которая имеет более низкую среднюю квадратичную невязку.
В любом случае предоставьте модель функции аппроксимации (которая является стартовой моделью для stepwiseglm).
Задайте модель с помощью одного из следующих методов.
| Имя | Тип модели |
|---|---|
'constant' | Модель содержит только постоянный (перехват) термин. |
'linear' | Модель содержит точку пересечения и линейные условия для каждого предиктора. |
'interactions' | Модель содержит точку пересечения, линейные условия и все продукты пар различных предикторов (без квадратов членов). |
'purequadratic' | Модель содержит точку пересечения, линейные условия и квадратные условия. |
'quadratic' | Модель содержит точку пересечения, линейные условия, взаимодействия и квадратные условия. |
' | Модель является полиномом со всеми терминами до степени i в первом предикторе, степень j во втором предикторе и т.д. Используйте цифры 0 через 9. Для примера, 'poly2111' имеет константу плюс все линейные и условия продукта, а также содержит условия с предиктором 1 в квадрате. |
Матрица терминов T является t -by- (p + 1) матрицей, задающей условия в модели, где t - количество членов, p - количество переменных предиктора, и + 1 учитывает переменную отклика. Значение T(i,j) - экспонента переменной j в терминах i.
Например, предположим, что вход включает три переменные предиктора x1, x2, и x3 и переменной отклика y в порядке x1, x2, x3, и y. Каждая строка T представляет собой один термин:
[0 0 0 0] - Постоянный срок или точка пересечения
[0 1 0 0] — x2; эквивалентно x1^0 * x2^1 * x3^0
[1 0 1 0] — x1*x3
[2 0 0 0] — x1^2
[0 1 2 0] — x2*(x3^2)
The 0 в конце каждого термина представляет переменную отклика. В целом векторе-столбце из нулей в матрице терминов представляет положение переменной отклика. Если у вас есть переменные предиктора и отклика в матрице и векторе-столбце, то вы должны включать 0 для переменной отклика в последнем столбце каждой строки.
Формула для спецификации модели является вектором символов или строковым скаляром вида
',y ~ <reservedrangesplaceholder0>'
y - имя отклика.
terms содержит
Имена переменных
+ чтобы включить следующую переменную
- чтобы исключить следующую переменную
: для определения взаимодействия, продукта терминов
* для определения взаимодействия и всех членов более низкого порядка
^ поднять предиктор в степень, точно как в * повторяется, так ^ включает также условия более низкого порядка
() к групповым терминам
Совет
Формулы включают постоянный (перехват) термин по умолчанию. Чтобы исключить постоянный термин из модели, включите -1 в формуле.
Примеры:
'y ~ x1 + x2 + x3' является линейной моделью с тремя переменными с точкой пересечения.
'y ~ x1 + x2 + x3 - 1' является линейной моделью с тремя переменными без точки пересечения.
'y ~ x1 + x2 + x3 + x2^2' является моделью с тремя переменными с точкой пересечения и x2^2 срок.
'y ~ x1 + x2^2 + x3' является тем же самым, что и в предыдущем примере, поскольку x2^2 включает в себя x2 срок.
'y ~ x1 + x2 + x3 + x1:x2' включает в себя x1*x2 срок.
'y ~ x1*x2 + x3' является тем же самым, что и в предыдущем примере, поскольку x1*x2 = x1 + x2 + x1:x2.
'y ~ x1*x2*x3 - x1:x2:x3' имеет все взаимодействия между x1, x2, и x3, кроме трехстороннего взаимодействия.
'y ~ x1*(x2 + x3 + x4)' имеет все линейные условия, плюс продукты x1 с каждой из других переменных.
Создайте подобранную модель используя fitglm или stepwiseglm. Выберите между ними как в Выбрать метод аппроксимации и Модель. Для обобщенных линейных моделей, отличных от моделей с нормальным распределением, дайте Distribution Пара "имя-значение" как в выборе обобщенной линейной модели и Ссылки функции. Для примера,
mdl = fitglm(X,y,'linear','Distribution','poisson') % or mdl = fitglm(X,y,'quadratic',... 'Distribution','binomial')
После подбора кривой модели исследуйте результат.
Линейная регрессионая модель показывает несколько диагностик, когда вы вводите его имя или вводите disp(mdl). Это отображение даёт некоторую базовую информацию, чтобы проверить, представляет ли подобранная модель данные адекватно.
Для примера подбирайте модель Пуассона к данным, построенным с двумя из пяти предикторов, не влияющих на ответ, и без точки пересечения термина:
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[.4;.2;.3]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson')
mdl =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x2 + x3 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.039829 0.10793 0.36901 0.71212
x1 0.38551 0.076116 5.0647 4.0895e-07
x2 -0.034905 0.086685 -0.40266 0.6872
x3 -0.17826 0.093552 -1.9054 0.056722
x4 0.21929 0.09357 2.3436 0.019097
x5 0.28918 0.1094 2.6432 0.0082126
100 observations, 94 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 44.9, p-value = 1.55e-08Заметьте, что:
Отображение содержит оценочные значения каждого коэффициента в Estimate столбец. Эти значения достаточно близки к истинным значениям [0;.4;0;0;.2;.3], за исключением, возможно, коэффициента x3 не страшно близко 0.
Существует стандартный столбец ошибок для оценок коэффициентов.
Отчетная pValue (которые получают из статистики t при допущении нормальных ошибок) для предикторов 1, 4 и 5 малы. Это три предиктора, которые использовались для создания данных отклика y.
The pValue для (Intercept), x2 и x3 больше 0,01. Эти три предиктора не использовались для создания данных отклика y. The pValue для x3 все просто кончено .05, так что может быть расценено как возможно значительное.
Отображение содержит статистику Хи-квадрат.
Диагностические графики помогают вам идентифицировать выбросы и увидеть другие проблемы в вашей модели или подгонке. Чтобы проиллюстрировать эти графики, рассмотрите биномиальную регрессию с функцией логистической ссылки.
Этот logistic model полезен для данных о пропорциях. Он определяет связь между p пропорции и весом, w:
log [p/( 1 - p)] = b 1 + b 2 w
Этот пример подходит биномиальной модели к данным. Данные получают из carbig.mat, который содержит измерения больших вагонов различной массы. Каждый вес в w имеет соответствующее количество автомобилей в total и соответствующее количество автомобилей с плохим пробегом в poor.
Разумно предположить, что значения poor следовать биномиальным распределениям с количеством испытаний, заданных total и процент успехов в зависимости от w. Это распределение может быть учтено в контексте логистической модели с помощью обобщенной линейной модели с журналом функции звена (µ/( 1 - µ)) = X b. Эта функция ссылки вызывается 'logit'.
w = [2100 2300 2500 2700 2900 3100 ... 3300 3500 3700 3900 4100 4300]'; total = [48 42 31 34 31 21 23 23 21 16 17 21]'; poor = [1 2 0 3 8 8 14 17 19 15 17 21]'; mdl = fitglm(w,[poor total],... 'linear','Distribution','binomial','link','logit')
mdl =
Generalized Linear regression model:
logit(y) ~ 1 + x1
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) -13.38 1.394 -9.5986 8.1019e-22
x1 0.0041812 0.00044258 9.4474 3.4739e-21
12 observations, 10 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 242, p-value = 1.3e-54Посмотрите, насколько хорошо модель подходит для данных.
plotSlice(mdl)
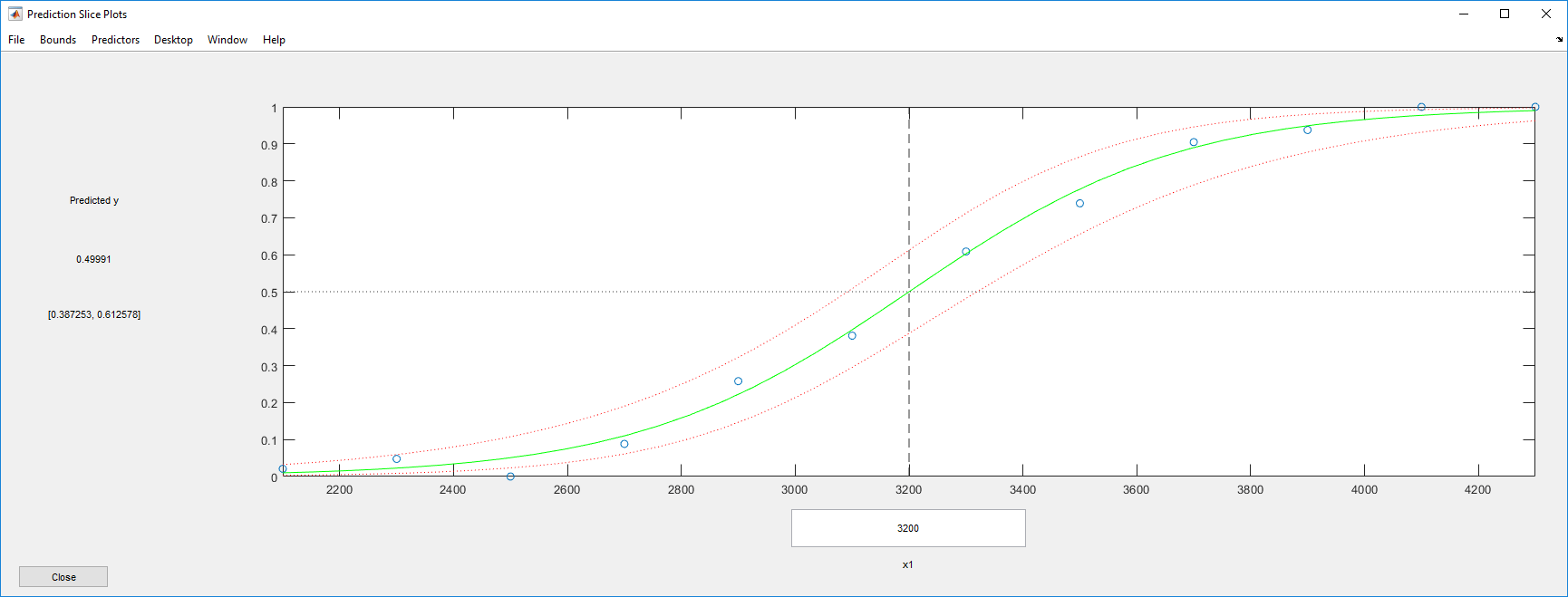
Подгонка выглядит достаточно хорошо, с довольно широкими доверительными границами.
Чтобы изучить дальнейшие детали, создайте график кредитного плеча.
plotDiagnostics(mdl)
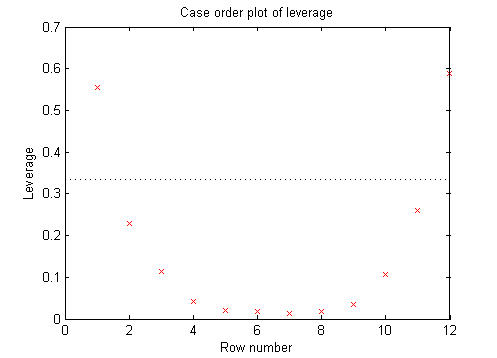
Это типично для регрессии с точками, упорядоченными переменной. Рычаги каждой точки на подгонке выше для точек с относительно крайними значениями предиктора (в любом направлении) и ниже для точек со средними значениями предиктора. В примерах с несколькими предикторами и с точками, не упорядоченными по значению предиктора, этот график может помочь вам определить, какие наблюдения имеют высокий рычаг, потому что они являются выбросами, измеренными их значениями предиктора.
Существует несколько остаточных графиков, которые помогут вам обнаружить ошибки, выбросы или корреляции в модели или данных. Простейшие остаточные графики являются графиком гистограммы по умолчанию, который показывает область значений невязок и их частот, и графиком вероятностей, который показывает, как распределение невязок сравнивается с нормальным распределением с совпадающим отклонением.
Этот пример показывает остаточные графики для модели Пуассона. Конструкция данных имеет два из пяти предикторов, не влияющих на ответ, и не имеет термина точки пересечения:
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson');
Исследуйте невязки:
plotResiduals(mdl)
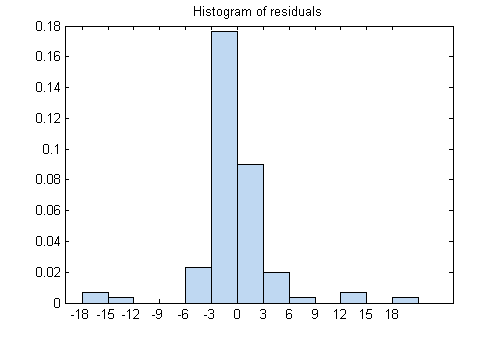
В то время как большинство невязок объединяются около 0, существует несколько близких ± 18. Поэтому рассмотрим другой график невязок.
plotResiduals(mdl,'fitted')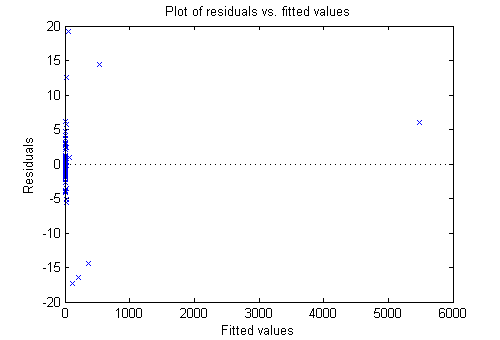
Большие невязки, по-видимому, не имеют большого отношения к размерам подобранных значений.
Возможно, вероятностный график более информативен.
plotResiduals(mdl,'probability')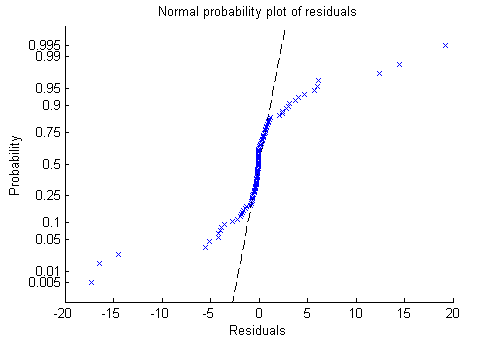
Теперь ясно. Невязки не следуют нормальному распределению. Вместо этого у них более толстые хвосты, так же как и базовое распределение Пуассона.
Этот пример показывает, как понять эффект каждый предиктор оказывает на регрессионую модель, и как изменить модель, чтобы удалить ненужные условия.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют второй и третий столбцы в X. Так что вы ожидаете, что модель не покажет большой зависимости от этих предикторов.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = fitglm(X,y,... 'linear','Distribution','poisson');
Исследуйте график среза откликов. Это отображает эффект каждого предиктора отдельно.
plotSlice(mdl)
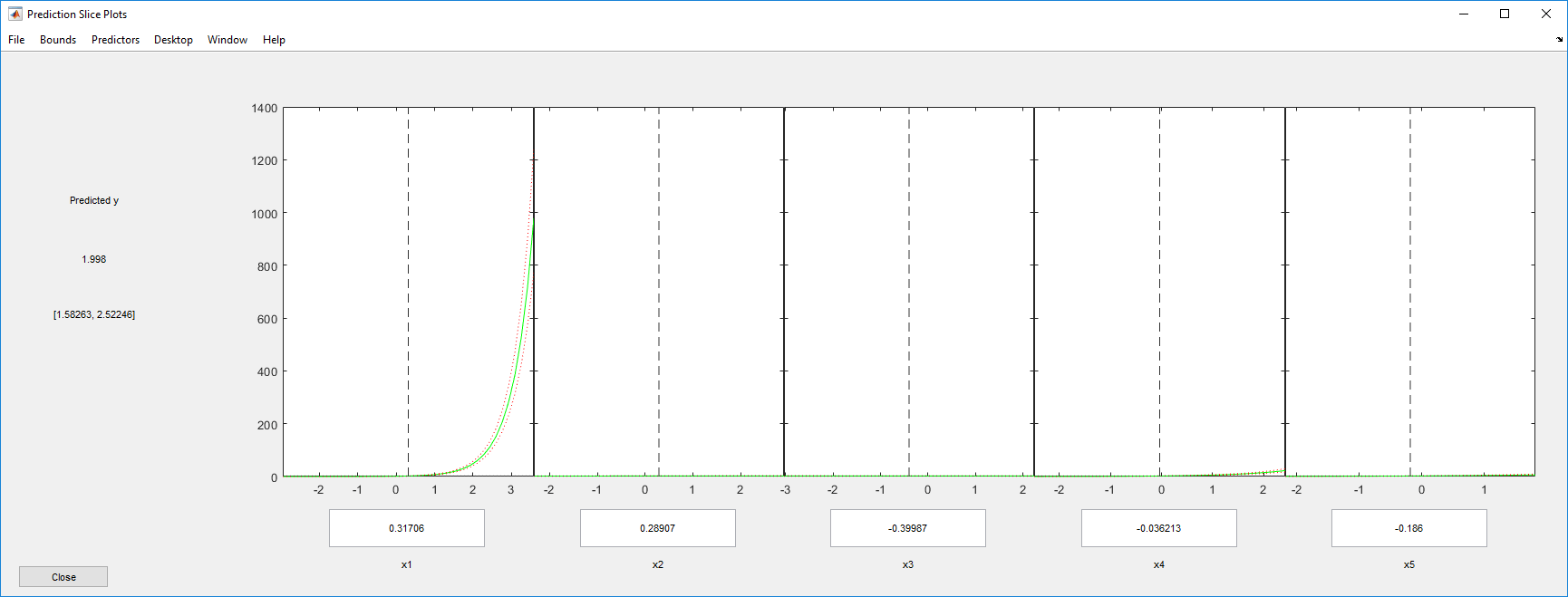
Шкала первого предиктора подавляет график. Отключите его с помощью меню Predictors.
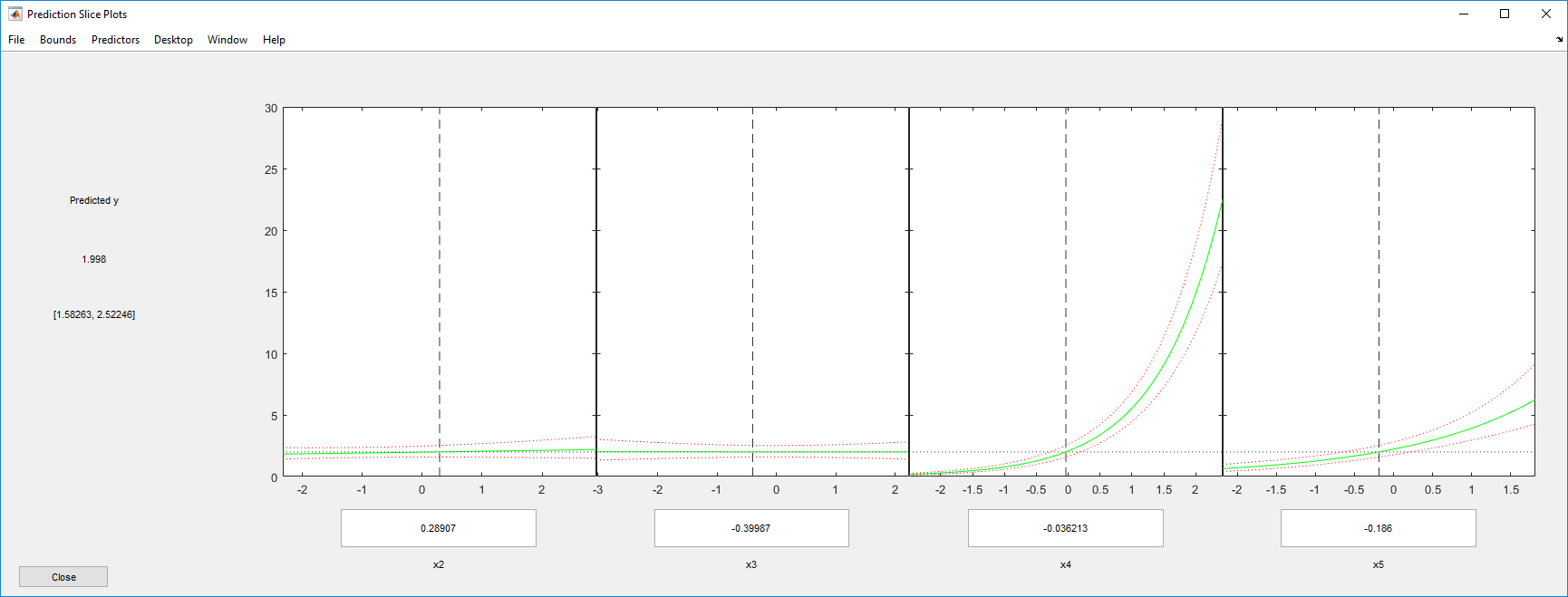
Теперь ясно, что предикторы 2 и 3 практически не влияют.
Можно перетащить отдельные значения предиктора, которые представлены штриховыми синими вертикальными линиями. Можно также выбрать между одновременными и не одновременными доверительными границами, которые представлены штриховыми красными кривыми. Перетаскивание линий предиктора подтверждает, что предикторы 2 и 3 практически не имеют эффекта.
Удалите ненужные предикторы, используя любой из removeTerms или step. Использование step может быть более безопасным, если существует неожиданная важность термина, который становится очевидным после удаления другого термина. Однако иногда removeTerms может быть эффективным, когда step не продолжается. В этом случае два дают одинаковые результаты.
mdl1 = removeTerms(mdl,'x2 + x3')mdl1 =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0mdl1 = step(mdl,'NSteps',5,'Upper','linear')
1. Removing x3, Deviance = 93.856, Chi2Stat = 0.00075551, PValue = 0.97807
2. Removing x2, Deviance = 96.333, Chi2Stat = 2.4769, PValue = 0.11553
mdl1 =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0Существует три способа использования линейной модели для предсказания реакции на новые данные:
predictThe predict метод дает предсказание средних откликов и, при запросе, доверительных границ.
В этом примере показано, как предсказать и получить доверительные интервалы на предсказаниях с помощью predict способ.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют второй и третий столбцы в X. Поэтому вы ожидаете, что модель не покажет большой зависимости от этих предикторов. Создайте модель пошагово, чтобы включить соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data
[ynew,ynewci] = predict(mdl,Xnew)ynew =
1.0e+04 *
0.1130
1.7375
3.7471
ynewci =
1.0e+04 *
0.0821 0.1555
1.2167 2.4811
2.8419 4.9407fevalКогда вы создаете модель из таблицы или массива набора данных, feval часто более удобно для предсказания средних откликов, чем predict. Однако feval не обеспечивает доверительных границ.
Этот пример показывает, как предсказать средние отклики с помощью feval способ.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют второй и третий столбцы в X. Поэтому вы ожидаете, что модель не покажет большой зависимости от этих предикторов. Создайте модель пошагово, чтобы включить соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); X = array2table(X); % create data table y = array2table(y); tbl = [X y]; mdl = stepwiseglm(tbl,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data ynew = feval(mdl,Xnew(:,1),Xnew(:,4),Xnew(:,5)) % only need predictors 1,4,5
ynew =
1.0e+04 *
0.1130
1.7375
3.7471Эквивалентно,
ynew = feval(mdl,Xnew(:,[1 4 5])) % only need predictors 1,4,5ynew =
1.0e+04 *
0.1130
1.7375
3.7471randomThe random метод генерирует новые значения случайного отклика для заданных значений предиктора. Распределением значений отклика является распределение, используемое в модели. random вычисляет среднее значение распределения из предикторов, оценочных коэффициентов и функции ссылки. Для распределений, таких как normal, модель также предоставляет оценку отклонения отклика. Для биномиального распределения и распределения Пуассона отклонение отклика определяется средним значением; random не использует отдельную оценку «дисперсии».
В этом примере показано, как моделировать ответы с помощью random способ.
Создайте модель из некоторых предикторов в искусственных данных. Данные не используют второй и третий столбцы в X. Поэтому вы ожидаете, что модель не покажет большой зависимости от этих предикторов. Создайте модель пошагово, чтобы включить соответствующие предикторы автоматически.
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson');
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0 2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0 3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
Сгенерируйте некоторые новые данные и оцените предсказания из данных.
Xnew = randn(3,5) + repmat([1 2 3 4 5],[3,1]); % new data
ysim = random(mdl,Xnew)ysim =
1111
17121
37457Предсказания из random являются выборками Пуассона, так же как и целые числа.
Оцените random снова метод, результат меняется.
ysim = random(mdl,Xnew)
ysim =
1175
17320
37126Отображение модели содержит достаточно информации, чтобы позволить кому-то другому воссоздать модель в теоретическом смысле. Для примера,
rng('default') % for reproducibility X = randn(100,5); mu = exp(X(:,[1 4 5])*[2;1;.5]); y = poissrnd(mu); mdl = stepwiseglm(X,y,... 'constant','upper','linear','Distribution','poisson')
1. Adding x1, Deviance = 2515.02869, Chi2Stat = 47242.9622, PValue = 0
2. Adding x4, Deviance = 328.39679, Chi2Stat = 2186.6319, PValue = 0
3. Adding x5, Deviance = 96.3326, Chi2Stat = 232.0642, PValue = 2.114384e-52
mdl =
Generalized Linear regression model:
log(y) ~ 1 + x1 + x4 + x5
Distribution = Poisson
Estimated Coefficients:
Estimate SE tStat pValue
(Intercept) 0.17604 0.062215 2.8295 0.004662
x1 1.9122 0.024638 77.614 0
x4 0.98521 0.026393 37.328 5.6696e-305
x5 0.61321 0.038435 15.955 2.6473e-57
100 observations, 96 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 4.97e+04, p-value = 0Вы также можете получить программный доступ к описанию модели. Для примера,
mdl.Coefficients.Estimate
ans =
0.1760
1.9122
0.9852
0.6132mdl.Formula
ans = log(y) ~ 1 + x1 + x4 + x5
[1] Collett, D. Modeling Binary Data. Нью-Йорк: Chapman & Hall, 2002.
[2] Добсон, А. Дж. Введение в обобщенные линейные модели. Нью-Йорк: Chapman & Hall, 1990.
[3] McCullagh, P., and J. A. Nelder. Обобщенные линейные модели. Нью-Йорк: Chapman & Hall, 1990.
[4] Нетер, Дж., М. Х. Кутнер, К. Дж. Нахтсхайм и У. Вассерман. Прикладные линейные статистические модели, четвертое издание. Ирвин, Чикаго, 1996.