Как и преобразование Фурье, непрерывное вейвлет (CWT) использует скалярные произведения, чтобы измерить подобие между сигналом и анализирующей функцией. В преобразовании Фурье функции анализа являются комплексными экспоненциалами, . Получившееся преобразование является функцией одной переменной, В краткосрочном преобразовании Фурье функции анализа являются оконными комплексными экспоненциалами, , и результат является функцией двух переменных. Коэффициенты STFT, представляйте матч между сигналом и синусоидой с угловой частотой ω в интервале указанной длины, сосредоточенной в τ.
В CWT анализирующей функцией является вейвлет, CWT сравнивает сигнал со сдвинутыми и сжатыми или растянутыми вариантами вейвлета. Растяжение или сжатие функции в совокупности называется расширением или масштабированием и соответствует физическому понятию шкалы. Сравнивая сигнал с вейвлетом в различных шкалах и положениях, вы получаете функцию двух переменных. Представление 2-D сигнала 1-D избыточно. Если вейвлет является комплексным, CWT является комплексной функцией шкалы и положения. Если сигнал является реальным, CWT является действительной функцией шкалы и положения. Для параметра шкалы, a > 0, и положения, b, CWT:
где обозначает комплексный сопряженный. Значения шкалы и положения не только влияют на коэффициенты CWT, но и выбор вейвлета также влияет на значения коэффициентов.
Путем непрерывного изменения значений параметра шкалы, a и параметра положения, b, вы получаете коэффициенты cwt C(a,b). Обратите внимание, что для удобства была подавлена зависимость коэффициентов CWT от функции и анализа вейвлета.
Умножение каждого коэффициента на соответственно масштабированный и сдвинутый вейвлет приводит к составным вейвлетам исходного сигнала.
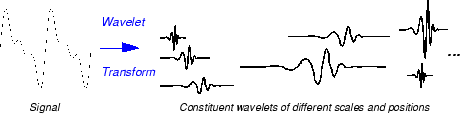
Существует много различных допустимых вейвлеты, которые могут использоваться в CWT. Хотя может показаться запутанным, что существует так много вариантов для анализа вейвлета, это на самом деле сила вейвлет-анализа. В зависимости от характеристик сигнала, которые вы пытаетесь обнаружить, вы можете выбрать вейвлет, который облегчает ваше обнаружение этой функции. Например, если вы пытаетесь обнаружить внезапные разрывы в вашем сигнале, можно выбрать один вейвлет. С другой стороны, если вы заинтересованы в нахождении колебаний с плавными онсетами и смещениями, вы можете свободно выбирать вейвлет, который более тесно соответствует этому поведению.
Как и концепция частоты, шкала является еще одним полезным свойством сигналов и изображений. Для примера можно проанализировать данные о температуре для изменений на различных шкалах. Вы можете посмотреть на изменения от года к году или от десятилетия к десятилетию. Конечно, вы можете изучить более мелкие (ежедневно) или более грубые изменения шкалы также. Некоторые процессы обнаруживают интересные изменения в течение длительного времени или пространственных шкалах, которые не видны в небольших временных или пространственных шкалах. Случается и обратная ситуация. Некоторые из наших восприимчивых способностей показывают инвариантность шкалы. Вы узнаете людей, которых знаете, независимо от того, смотрите ли вы на большой портрет, или маленькую фотографию.
Чтобы выйти за рамки разговорных описаний, таких как «растяжение» или «сужение», мы вводим фактор шкалы, часто обозначаемый букву a. Коэффициент шкалы является по своей сути положительной величиной, a > 0. Для синусоидов эффект фактора шкалы очень легко увидеть.
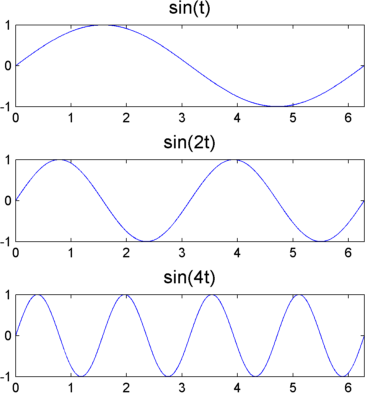
В sin (в) шкала является обратной радианой частоты, a.
Коэффициент шкалы работает точно так же с вейвлетами. Чем меньше коэффициент шкала, тем больше «сжимается» вейвлет. И наоборот, чем больше шкала, тем больше растягивается вейвлет. Следующий рисунок иллюстрирует это для вейвлетов в шкалах 1,2 и 4.
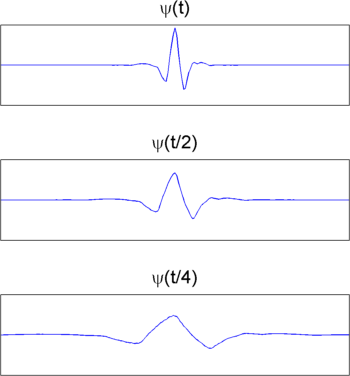
Эта общая обратная связь между шкалой и частотой сохранена для сигналов в целом.
Представление шкалы времени является не только другим способом просмотра данных, но и очень естественным способом просмотра данных, полученных от большого количества природных явлений.
Между шкалой и частотой явно существует связь. Напомним, что более длинные шкалы соответствуют наиболее «растянутым» вейвлетам. Чем более растянутый вейвлет, тем большой фрагмент сигнала, с которой он сравнивается, и, следовательно, более грубые функции сигнала, измеренные вейвлет-коэффициентами.

Результирующие, общее соответствие между шкалой и частотой:
Малая шкала a ⇒ Сжатый вейвлет ⇒ Быстро изменяющиеся детали ⇒ Высокая частота
Длинная шкала a ⇒ Растянутый вейвлет ⇒ Медленно изменяющиеся, грубые функции ⇒ Низкая частота
Хотя существует общая связь между шкалой и частотой, точных отношений не существует. Пользователи, знакомые с анализом Фурье, часто хотят задать отображение между вейвлет в заданной шкале с заданным периодом дискретизации на частоту в герце. Вы можете сделать это только в общем смысле. Поэтому лучше говорить о псевдочастоте, соответствующей шкале. Программное обеспечение Wavelet Toolbox™ обеспечивает две функции centfrq и scal2frq, что позволяет вам найти эти приблизительные отношения шкала-частота для заданных вейвлетов и шкал.
Основной подход идентифицирует пиковую степень в преобразовании Фурье вейвлета как его центральную частоту и делит это значение на продукт шкалы и интервала дискретизации. Посмотрите scal2frq для получения дополнительной информации. В следующем примере показано соответствие между предполагаемой центральной частотой db8 вейвлет и синусоида той же частоты.
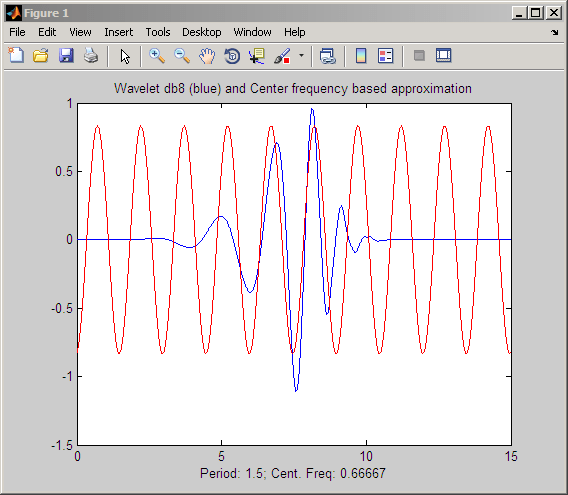
Зависимость между шкалой и частотой в CWT также исследуется в Непрерывном Преобразовании Вейвлет как Полосно-Пропускном Фильтре.
Сдвиг вейвлета просто означает задержку (или продвижение) его начала. Математически задержка функции f (t) на k представлена f (t - k):
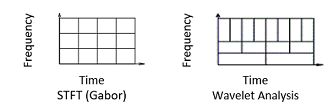
При кратковременном преобразовании Фурье STFT описывается как оконное отображение сигнала для создания локального частотного анализа. Недостатком подхода STFT является то, что размер окна является постоянным. Существует компромисс в выборе размера окна. Более длинное временное окно улучшает разрешение частоты, в то же время приводя к худшему разрешению времени, потому что преобразование Фурье теряет разрешение все время в течение длительности окна. И наоборот, более короткое временное окно улучшает локализацию времени, в то же время приводя к более низкому разрешению частоты.
Вейвлет анализ представляет следующий логический шаг: метод оконной обработки с переменными областями. Вейвлет позволяет использовать большие временные интервалы, где вы хотите более точную низкочастотную информацию и более короткие области, где вы хотите высокочастотную информацию.

Следующий рисунок контрастирует с различными способами STFT и вейвлет разлагают частотно-временную плоскость.