Критически выбранные и переизбранные банки вейвлет

Вейвлеты фильтра являются особыми случаями многоскоростного фильтра банков, называемых древовидными банками фильтров. В группе фильтров к входному сигналу прикладываются два или более фильтров, и выходы фильтра обычно понижают дискретизацию. Следующий рисунок иллюстрирует два этапа или уровня критически выбранной двухканальной древовидной группы фильтров анализа. Фильтры изображены в z области.

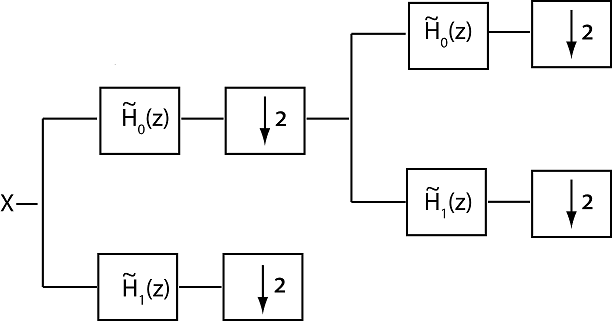
Система фильтров функционирует, ${\tilde{H}}_{0} (z)$ и ${\tilde{H}}_{1} (z)$ , обычно предназначены для приблизительно разбиения входного сигнала, X, на несвязанные поддиапазоны. В вейвлет банках фильтров, фильтр ${\tilde{H}}_{0} (z)$ lowpass, или масштабирование, фильтр, с отличной от нуля частотной характеристикой на интервале [-π/2, π/2] радианы/выборка или [-1/4, 1/4] циклы/выборка. Фильтр ${\tilde{H}}_{1} (z)$ highpass, или вейвлет, фильтр, с отличной от нуля частотной характеристикой на интервале [-π,-π/2] ∪ [π/2, π] радианы/выборка или [-1/2,-1/4] ∪ [1/4, 1/2] циклы/выборка. Группа фильтров итератирует на выходе фильтра lowpass анализа, получая последующие уровни, получая приблизительную октавно-полосную фильтрацию входа. Эти два фильтра анализа не идеальны, что приводит к сглаживанию, которое должно быть отменено соответствующим образом разработанными фильтрами синтеза для идеальной реконструкции. Для ортогональной группы фильтров объединение масштабирующего фильтра и его четных сдвигов и вейвлет и его четных сдвигов образует ортонормированный базис для пространства квадратно-суммируемых последовательностей, $ℓ^{2} (ℤ)$ . Фильтры синтеза являются обратными по времени и сопряженными с фильтрами анализа. Для биортогональных блоков фильтров фильтры синтеза и их ровные сдвиги образуют взаимный, или двойной, базис к фильтрам анализа. С помощью двух фильтров анализа понижающая дискретизация выхода каждого фильтра анализа на два на каждом этапе гарантирует, что общее количество выхода проб равняется количеству входа проб. Случай, когда количество фильтров анализа равно коэффициенту понижающей дискретизации, упоминается как критическая выборка. Группа фильтров анализа, где количество каналов больше, чем коэффициент понижающей дискретизации, является группой фильтров с избыточной дискретизацией.

Преобразование

Вейвлета двойной плотности

Следующий рисунок иллюстрирует два уровня банка фильтров с избыточной дискретизацией с тремя каналами и коэффициентом понижающей дискретизации два. Фильтры изображены в z области.

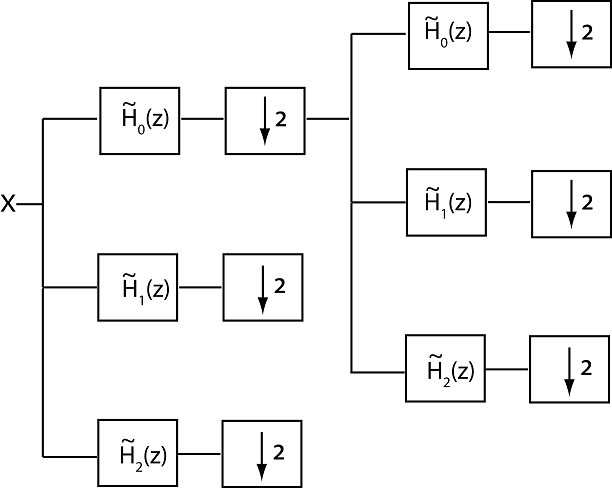
Предположим, что фильтр ${\tilde{H}}_{0} (z)$ , является lowpass полупрозрачным фильтром и фильтрами ${\tilde{H}}_{1} (z)$ и ${\tilde{H}}_{2} (z)$ являются высокочастотными полупрозрачными фильтрами.

Предположим, что три фильтра вместе с соответствующими синтезирующими фильтрами образуют идеальную группу восстановительных фильтров. Если дополнительно, ${\tilde{H}}_{1} (z)$ и ${\tilde{H}}_{2} (z)$ сгенерировать вейвлеты, которые удовлетворяют следующему отношению

$ψ_{1} (t) = ψ_{2} (t - 1 / 2),$

группа фильтров реализует вейвлет двойной плотности. Предшествующее условие гарантирует, что целое число переведет одно падение вейвлета на половину между целыми переводами второго вейвлета. В теоретических терминах кадра вейвлет двойной плотности реализует плотное расширение системы координат.

Следующий код иллюстрирует два вейвлета, используемых в вейвлет-преобразовании двойной плотности.

x = zeros(256,1);
df = dtfilters('filters1');
wt1 = dddtree('ddt',x,5,df,df);
wt2 = dddtree('ddt',x,5,df,df);
wt1.cfs{5}(5,1,1) = 1;
wt2.cfs{5}(5,1,2) = 1;
wav1 = idddtree(wt1);
wav2 = idddtree(wt2);
plot(wav1); hold on;
plot(wav2,'r'); axis tight;
legend('\psi_1(t)','\psi_2(t)')

Вы не можете выбрать два фильтра вейвлета произвольно, чтобы реализовать преобразование вейвлета с двойной плотностью. Три фильтра анализа и синтеза должны удовлетворять идеальным условиям реконструкции (PR). Для трех реальных фильтров условия PR:

$\begin{array}{l} H_{0} (z) H_{0} (1 / z) + H_{1} (z) H_{1} (1 / z) + H_{2} (z) H_{2} (1 / z) = 2 \\ H_{0} (z) H_{0} (- 1 / z) + H_{1} (z) H_{1} (- 1 / z) + H_{2} (z) H_{2} (- 1 / z) = 0 \end{array}$

Можно получить вейвлет систем координат анализа и синтеза для преобразования вейвлета с двойной плотностью с 6 и 12 тапами, используя dtfilters.

[df1,sf1] = dtfilters('filters1');
[df2,sf2] = dtfilters('filters2');

df1 и df2 являются трехколоночными матрицами, содержащими фильтры анализа. Первый столбец содержит фильтр масштабирования, а столбцы два и три содержат вейвлет. Соответствующие фильтры синтеза состоят из sf1 и sf2.

Смотрите [4] и [5] для получения дополнительной информации о том, как сгенерировать системы координат вейвлета для преобразования вейвлета с двойной плотностью.

Основными преимуществами преобразования вейвлета двойной плотности по сравнению с критически выбранными дискретными вейвлетами преобразования являются

Снижение чувствительности к сдвигу
Уменьшенные прямоугольные программные продукты в 2-D преобразовании
Более плавные вейвлеты для заданного количества моментов исчезновения

Основными недостатками являются:

Увеличение вычислительных затрат
Неортогональное преобразование

Кроме того, проявляя меньшую чувствительность к сдвигу, чем критически выбранное DWT, double-density DWT не является инвариантным к сдвигу, как комплексное двухдревовидное вейвлет. Преобразованию вейвлета с двойной плотностью также не хватает направленной избирательности ориентированных преобразований вейвлета с двойственным деревом.

Двухдревовидный комплексный Вейвлет преобразование

Критически выбранное дискретное вейвлет (DWT) страдает от отсутствия инвариантности сдвига в 1-D и направленной чувствительности в N-D. Можно уменьшить эти недостатки при помощи приблизительно аналитических вейвлеты. Аналитический вейвлет определяется как

$ψ_{c} (t) = ψ_{r} (t) + j ψ_{i} (t)$

где j обозначает модуль мнимой. Мнимая часть вейвлета, _ψi(t), является преобразованием Гильберта действительной части, _ψr(t). В частотный диапазон аналитический вейвлет имеет поддержку только на одной половине оси частоты. Это означает, что _ψc(t) аналитического вейвлета имеет только половину полосы пропускания реального вейвлета _ψr(t).

Невозможно получить точно аналитические вейвлеты, сгенерированные конечная импульсная характеристика. Преобразования Фурье компактно поддерживаемых вейвлетов не могут исчезнуть ни на одном наборе ненулевых измерений. Это означает, что преобразование Фурье не может быть нулем на отрицательной частотной оси. Кроме того, эффективная двухканальная реализация банка фильтров DWT происходит из следующего идеального условия реконструкции для масштабирующего фильтра, $H_{0} (e^{j ω})$ , мультиразрешения (MRA)

$| H_{0} (e^{j ω}) |^{2} + | H_{0} (e^{j (ω + π)}) |^{2} = 2.$

Если вейвлет, сопоставленный с MRA, аналитический, функция масштабирования также аналитическая. Это подразумевает, что

$H_{0} (e^{j ω}) = 0 - π \leq ω < 0,$

из чего следует, что $| H_{0} (e^{j ω}) |^{2} = 2 0 \leq ω \leq π .$ Результатом является то, что масштабирующий фильтр является allpass.

Предыдущие результаты показывают, что вы не можете найти компактно поддерживающий вейвлет, определяемый конечная импульсная характеристика, который является точно аналитическим. Однако можно получить вейвлеты, которые являются приблизительно аналитическими, путем объединения двух древовидно структурированных банков фильтров, пока фильтры в двухдревовидном преобразовании тщательно построены, чтобы удовлетворить определенные обстоятельства [1], [6].

Двухдревовидный комплексный вейвлет преобразования реализован с двумя отдельными двухканальными конечными импульсными характеристиками фильтрующими банками. Выход одной группы фильтров рассматривается как действительная часть, в то время как выход другой группы фильтров является мнимой частью. Поскольку двойственное древовидное комплексное вейвлет использует две критически выбранные группы фильтров, избыточность равна 2^d для d-мерного сигнала (изображения). Существуют несколько критических факторов при реализации двойного древовидного комплексного вейвлет. Для удобства обратитесь к двум деревьям как: Tree A и Tree B.

Фильтры анализа на первом этапе каждой группы фильтров должны отличаться от фильтров, используемых на последующих этапах в обоих деревьях. Не важно, какие масштабные и вейвлет вы используете в двух деревьях для стадии 1. Можно использовать одинаковые масштабные и вейвлет первого каскада в обоих деревьях.
Масштабирующий фильтр в дереве B для каскадов ≥ 2 должен аппроксимировать 1/2 задержки выборки масштабирующего фильтра в дереве A. Условие задержки половины выборки является необходимым и достаточным условием для того, чтобы соответствующий вейвлет дерева B был преобразованием Гильберта вейвлета Tree A. [3].

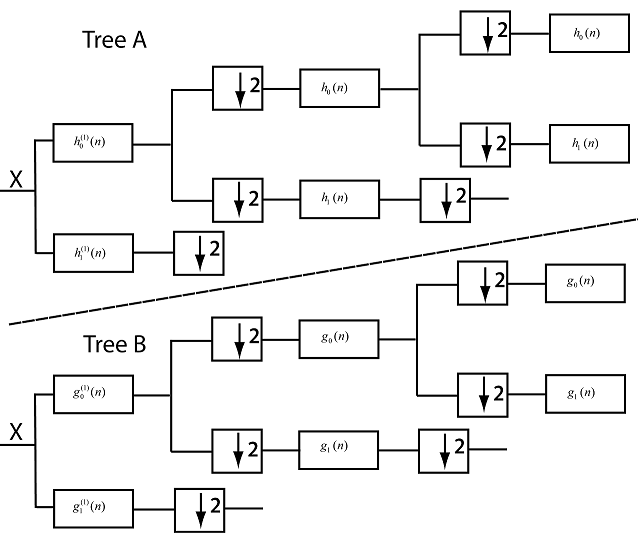
Следующий рисунок иллюстрирует три этапа группы фильтров анализа для 1-D двухдревовидного комплексного вейвлет. Фильтры конечной импульсной характеристики масштабирования для двух деревьев обозначены ${h_{0} (n), g_{0} (n)}$ . Фильтры конечной импульсной характеристики вейвлета для двух деревьев обозначены ${h_{1} (n), g_{1} (n)}$ . Два масштабирующих фильтра разработаны, чтобы приблизительно удовлетворить условию задержки половины выборки

$g_{0} (n) = h_{0} (n - 1 / 2)$

Надстрочный индекс (1) означает, что фильтры первой ступени должны отличаться от фильтров, используемых на последующих стадиях. Для первого этапа можно использовать любую допустимую пару масштабирующе-вейвлет-фильтра. Фильтры ${h_{0} (n), g_{0} (n)}$ не может быть произвольными фильтрами масштабирования и обеспечивает преимущества использования приблизительно аналитических вейвлеты.

2-D преобразования двух древовидных вейвлет

Двойное древовидное вейвлет-преобразование с приблизительно аналитическими вейвлетами предлагает существенные преимущества по сравнению с разделяемым 2-D DWT для обработки изображений. Традиционный разделяемый 2-D DWT страдает от шахматных программных продуктов из-за симметричной частотной поддержки действительных (неаналитических) функций масштабирования и вейвлетов. Кроме того, критически выбранной разделяемой 2-D DWT не хватает инвариантности сдвига так же, как и 1-D критически выбранной DWT. Программное обеспечение Wavelet Toolbox™ поддерживает два варианта двойного древовидного 2-D вейвлет, действительное ориентированное двойственное древовидное вейвлет и ориентированное 2-D двойное древовидное комплексное вейвлет. Оба подробно описаны в [6].

Действительное ориентированное двухдревовидное преобразование состоит из двух разделяемых (фильтрация строк и столбцов) вейвлет фильтрующих банков, работающих параллельно. Комплексное ориентированное 2-D вейвлет требует четырех разделяемых банков вейвлет и поэтому технически не является преобразованием двойственного дерева. Однако он упоминается как преобразование двойственного дерева, потому что это естественное расширение 1-D комплексного преобразования двойственного дерева. Чтобы реализовать реальное ориентированное двухдревовидное вейвлет, используйте 'realdt' опция в dddtree2. Чтобы реализовать ориентированное комплексное двухдревовидное преобразование, используйте 'cplxdt' опция.

Как реальные, так и ориентированные комплексные преобразования двойственного дерева чувствительны к направленным функциям в изображении. Только ориентированное комплексное преобразование двойственного дерева является приблизительно инвариантным сдвигом. Инвариация сдвига не является функцией, которым обладает действительное ориентированное двухдревовидное преобразование.

Двухдревовидное преобразование Вейвлета двойной плотности

Двойственное древовидное вейвлет двойной плотности комбинирует свойства вейвлет двойной плотности и двойного древовидного вейвлет [2].

В 1-D двухдревовидное вейвлет двойной плотности состоит из двух трехканальных фильтрующих блоков. Два вейвлета в каждом дереве удовлетворяют условиям, описанным в Double-Density Wavelet Transform. В частности, целое число переводит одно вейвлет-падение на половину между целым числом переводов второго вейвлета. Кроме того, вейвлеты в дереве B являются приблизительным преобразованием Гильберта вейвлетов в дереве A. Чтобы реализовать двойное древовидное вейвлет-преобразование двойной плотности для 1-D сигналов, используйте 'cplxdddt' опция в dddtree. Подобен вейвлет преобразованию двойственного дерева, вейвлета преобразование двойного дерева с двойной плотностью обеспечивает как действительный так и комплексный вейвлет преобразования в 2-D. Чтобы получить действительное ориентированное двойное древовидное вейвлет двойной плотности, используйте 'realdddt' опция в dddtree2. Чтобы получить комплексное ориентированное двойное древовидное вейвлет двойной плотности, используйте 'cplxdddt' опция.

Ссылки

[1] Kingsbury, N.G. «Complex Wavelets for Shift Invariant Analysis and Filtering of Signals». Журнал прикладного и вычислительного гармонического анализа. Том 10, № 3, май 2001, стр. 234-253.

[2] Selesnick, I. «The Double-Density Dual-Tree Wavelet Transform». IEEE^® Транзакции по обработке сигналов. Том 52, № 5, май 2004 года, стр. 1304-1314.

[3] Selesnick, I. «The Design of Approvate Преобразование Гильберта Pairs of Wavelet Bases». Транзакции IEEE по обработке сигналов, том 50, номер 5, стр. 1144-1152.

[4] Selesnick, I. «The Double Density DWT» Wavelets in Signal and Image Analysis: From Theory to Practice (A.A Petrosian, F.G. Meyer, eds.). Norwell, MA: Kluwer Academic Publishers:, 2001.

[5] Abdelnour, F. «Symmetric Wavelets Dyadic Siblings and Dual Frames» Signal Processing, Vol. 92, Number 5, 2012, pp. 1216-1225.

[6] Селесник, я,. Р. Г. Баранюка и Н. Г. Кингсбери. «Двухдревовидный комплексный Вейвлет преобразования». Журнал обработки сигналов IEEE. Том 22, № 6, ноябрь 2005, стр. 123-151.

[7] Vetterli, M. «Wavelets, Approximation, and Compression». Журнал обработки сигналов IEEE, том 18, № 5, сентябрь 2001, стр. 59-73.

См. также

dddtree | dddtree2 | dualtree | dualtree2

Документация