В этом разделе рассматриваются функции 2-D дискретного вейвлет с помощью программного обеспечения Wavelet Toolbox™. Тулбокс предоставляет эти функции для анализа изображений. Для получения дополнительной информации см. страницы с описанием функций.
Примечание
В этом разделе презентация и примеры используют 2-D массивы, соответствующие индексированным представлениям изображений. Однако описанные функции также доступны при использовании изображений truecolor, которые представлены m-by- n-by-3 массива uint8. Для получения дополнительной информации о форматах изображений смотрите Wavelets: Working with Images.
Имя функции | Цель |
|---|---|
Вейвлет изображения шумоподавления | |
Предоставьте значения по умолчанию для шумоподавления и сжатия | |
Штрафованный порог для вейвлет- 1-D или 2-D шумоподавление | |
Пороги для вейвлет- 2-D с использованием стратегии Бирже-Массарта | |
Вейвлет- шумоподавление и сжатие | |
Диспетчер параметров порога |
В этом разделе вы узнаете
Как загрузить изображение
Как анализировать изображение
Как выполнить одноуровневое и многоуровневое разложение и реконструкции изображений (только для командной строки)
Как использовать функции квадратного и древовидного режима (только для GUI)
Как увеличить изображение подробно (только для графического интерфейса)
Как сжать изображение
Этот пример показывает, как можно использовать 2-D вейвлет для эффективного сжатия изображения, не жертвуя его ясностью.
Примечание: Вместо прямого использования image(I) для визуализации изображения I, мы используем image(wcodemat(I)), которая отображает измененную версию I обеспечение более четкого представления деталей и приближений (см. wcodemat).
Загрузка изображения.
load wbarb whos X map
Name Size Bytes Class Attributes X 256x256 524288 double map 192x3 4608 double
Отобразите изображение.
image(X) colormap(map) colorbar

Если палитра гладкая, вейвлет-преобразование может быть непосредственно применено к индексированному изображению; в противном случае индексированное изображение должно быть преобразовано в формат полутонового цвета. Для получения дополнительной информации смотрите Вейвлеты: Работа с изображениями. Поскольку палитра гладкая в этом изображении, теперь можно выполнить разложение.
Выполните одноуровневое вейвлет изображения с помощью bior3.7 вейвлет. Матрица коэффициентов cA1 являются приближениями. Горизонтальные, вертикальные и диагональные детали указаны в матрицах cH1, cV1, и cD1, соответственно.
wv = 'bior3.7';
[cA1,cH1,cV1,cD1] = dwt2(X,wv);Использование idwt1 чтобы создать приближения и детали из коэффициентов. (Примечание: Вы также можете использовать upcoef2.
sx = size(X); A1 = idwt2(cA1,[],[],[],wv,sx); H1 = idwt2([],cH1,[],[],wv,sx); V1 = idwt2([],[],cV1,[],wv,sx); D1 = idwt2([],[],[],cD1,wv,sx);
Отобразите приближения и детали.
figure subplot(2,2,1) image(wcodemat(A1,192)) title('Approximation A1') subplot(2,2,2) image(wcodemat(H1,192)) title('Horizontal Detail H1') subplot(2,2,3) image(wcodemat(V1,192)) title('Vertical Detail V1') subplot(2,2,4) image(wcodemat(D1,192)) title('Diagonal Detail D1') colormap(map)

Регенерируйте изображение одноуровневым обратным дискретным вейвлет. Подтвердите, что различие между регенерированным и исходным изображениями небольшая.
Xrec = idwt2(cA1,cH1,cV1,cD1,wv); max(abs(X(:)-Xrec(:)))
ans = 1.4211e-13
Выполните вейвлет изображения уровня 2 с помощью той же bior3.7 вейвлет. Коэффициенты всех компонентов разложения второго уровня (то есть приближения второго уровня и первых двух уровней детализации) возвращаются конкатенированными в один вектор, C. Аргументы в S - матрица бухгалтерии, которая отслеживает размеры каждого компонента.
[c,s] = wavedec2(X,2,wv);
Извлеките коэффициенты приближения уровня 2. Извлеките коэффициенты детализации первого и второго уровней.
cA2 = appcoef2(c,s,wv,2); [cH2,cV2,cD2] = detcoef2('all',c,s,2); [cH1,cV1,cD1] = detcoef2('all',c,s,1);
Восстановите приближение уровня 2 и детали уровней 1 и 2.
A2 = wrcoef2('a',c,s,wv,2); H1 = wrcoef2('h',c,s,wv,1); V1 = wrcoef2('v',c,s,wv,1); D1 = wrcoef2('d',c,s,wv,1); H2 = wrcoef2('h',c,s,wv,2); V2 = wrcoef2('v',c,s,wv,2); D2 = wrcoef2('d',c,s,wv,2);
Отобразите приближение и детали.
figure subplot(2,4,1) image(wcodemat(A1,192)) title('Approximation A1') subplot(2,4,2) image(wcodemat(H1,192)) title('Horizontal Detail H1') subplot(2,4,3) image(wcodemat(V1,192)) title('Vertical Detail V1') subplot(2,4,4) image(wcodemat(D1,192)) title('Diagonal Detail D1') subplot(2,4,5) image(wcodemat(A2,192)) title('Approximation A2') subplot(2,4,6) image(wcodemat(H2,192)) title('Horizontal Detail H2') subplot(2,4,7) image(wcodemat(V2,192)) title('Vertical Detail V2') subplot(2,4,8) image(wcodemat(D2,192)) title('Diagonal Detail D2') colormap(map)

Сжать изображение. Использование ddencmp вычисление параметров и wdencmp по умолчанию для выполнения фактического сжатия.
[thr,sorh,keepapp] = ddencmp('cmp','wv',X); [Xcomp,CXC,LXC,PERF0,PERFL2] = ... wdencmp('gbl',c,s,wv,2,thr,sorh,keepapp);
Сравните сжатое изображение с оригинальным изображением.
fprintf('Percentage of wavelet coefficients set to zero: %.4f\nPercentage of energy preserved: %.4f\n',... PERF0,PERFL2);
Percentage of wavelet coefficients set to zero: 49.8011 Percentage of energy preserved: 99.9817
figure subplot(121) image(X) title('Original Image') axis square subplot(122) image(Xcomp) title('Compressed Image') axis square colormap(map)

Обратите внимание, что, даже несмотря на то, что сжатое изображение построено только из примерно вдвое меньшего числа ненулевых коэффициентов вейвлета, чем исходное, почти нет обнаруживаемого ухудшения качества изображения.
В этом разделе мы исследуем то же изображение, что и в предыдущем разделе, но для анализа изображения мы используем приложение Wavelet Analyzer.
Запустите 2-D Wavelet Analysis Tool.
Из MATLAB® приглашение, тип waveletAnalyzer.
Появится главный вейвлет Инструмент.
Выберите меню Вейвлета 2-D элементов. Появляется инструмент дискретного вейвлет для 2-D данных изображения.

Загрузка изображения.
В командной строке MATLAB введите
load wbarb
X переменная. Нажмите кнопку ОК, чтобы импортировать изображение.Изображение загружается в инструмент Wavelet 2-D.
Проанализируйте изображение.
Используя меню «Вейвлет» и «Уровень», расположенные справа вверху, определите семейство вейвлет, тип вейвлета и количество уровней, которые будут использоваться для анализа.
Для этого анализа выберите bior3.7 вейвлет на уровне 2.

Нажмите кнопку Analyze. После паузы для расчетов инструмент Wavelet 2-D отображает его анализ.
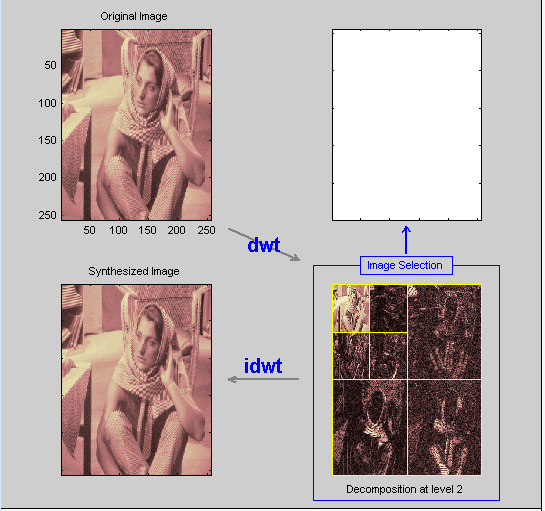
Использование функций квадратного режима
По умолчанию анализ появляется в «Квадратном режиме». Этот режим включает четыре различных отображений. В верхнем левом - оригинальное изображение. Ниже приведено изображение, восстановленное из различных приближений и деталей. Справа внизу находится разложение, показывающее коэффициенты самого грубого приближения и все горизонтальные, диагональные и вертикальные коэффициенты детализации. Наконец, пространство визуализации в правом верхнем углу отображает любой компонент анализа, на который вы хотите взглянуть более внимательно.
Щелкните на любом компоненте разложения в правом нижнем окне.
Синяя граница подсвечивает выбранный компонент. В правом нижнем углу окна 2-D Вейвлет находится набор из трех кнопок с надписью «Операций на выбранном изображении». Обратите внимание, что при повторном клике по тому же компоненту он будет отменен, а синяя граница исчезнет.

Нажмите кнопку Визуализация.
Выбранное изображение отображается в области визуализации. Вы видите необработанные, непоследовательные 2-D вейвлет. Используя другие кнопки, можно отобразить восстановленную версию выбранного компонента изображения или просмотреть выбранный компонент в полноэкранном разрешении.
Использование функций древовидного режима
В меню View Mode выберите Tree.
Ваше отображение изменится, чтобы открыть следующее.

Это та же информация, показанная в квадратном режиме, с дополнительно всеми коэффициентами приближения, но организованная, чтобы подчеркнуть древовидную структуру разложения. Различные кнопки и меню работают точно так же, как и в квадратном режиме.
Масштабирование по деталям
Перетащите резиновый ленточный ящик (удерживая нажатой левую кнопку мыши) над фрагментом изображения, которое необходимо увеличить.
Нажмите кнопку XY + (расположенную в нижней части экрана) для изменения масштаба по горизонтали и вертикали.
![]()
Инструмент Вейвлета 2-D увеличивает отображаемые изображения.
Чтобы вернуться к исходному увеличению, нажмите кнопку «История» < < -.
Нажмите кнопку «Сжатие», расположенную в правом верхнем углу окна Вейвлета 2-D. Появится окно Wavelet 2-D Compression.
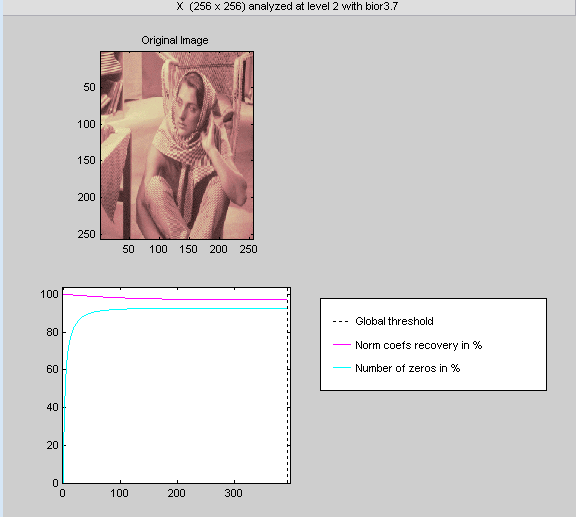
Инструмент автоматически выбирает уровни порога, чтобы обеспечить хороший начальный баланс между сохранением энергии изображения и минимизацией количества коэффициентов, необходимых для представления изображения.
Однако можно также настроить пороги вручную с помощью опции По уровню (By Level), а затем ползунки или правки, соответствующие каждому уровню.
В данном примере выберите опцию By Level thresholding и выберите метод Remove near 0 из меню Select thresholding method.
Отобразится следующее окно.
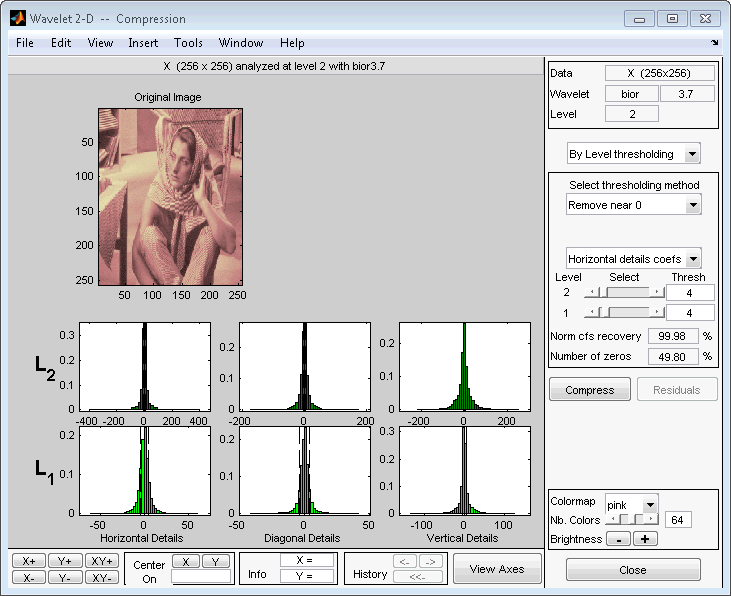
Выберите из меню направления, хотите ли вы настроить пороги для горизонтальных, диагональных или вертикальных деталей. Чтобы внести фактические корректировки для каждого уровня, используйте ползунки или левую кнопку мыши, чтобы непосредственно перетащить штриховые линии.
Чтобы сжать оригинальное изображение, нажмите кнопку «Сжатие». После паузы для расчетов сжатое изображение отображается рядом с исходным. Заметьте, что сжатие устраняет почти половину коэффициентов, но не появляется обнаруживаемого ухудшения изображения.

Показать невязки.
Из инструмента Вейвлета 2-D сжатия нажмите кнопку Невязок. Появится окно Подробнее об невязках для вейвлет 2-D сжатия.
Отображаемая статистика включает показатели тенденции (среднее, режим, медиана) и дисперсии (область значений, стандартное отклонение). В сложение инструмент предоставляет диаграммы частотного распределения (гистограммы и совокупные гистограммы). Тот же инструмент существует и для инструмента Wavelet 2-D Шумоподавление.
Примечание
Статистика, отображаемая на приведенном выше рисунке, связана с отображаемым изображением, но не с исходным. Обычно эта информация является такой же, но в некоторых случаях эффекты ребра могут привести к тому, что оригинальное изображение будет немного обрезано. Чтобы увидеть точную статистику, используйте функции командной строки, чтобы получить желаемое изображение и затем примените желаемую статистическую функцию (ы) MATLAB.
Графический инструмент Wavelet 2-D позволяет вам импортировать информацию с диска и экспортировать информацию на диск, если вы придерживаетесь соответствующих форматов файлов.
Можно сохранить синтезированные изображения, коэффициенты и разложения с инструмента Wavelet 2-D на диск, где информацией можно манипулировать и позже повторно импортировать в графический инструмент.
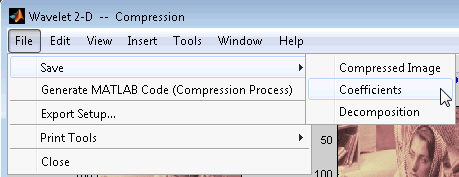
Сохранение синтезированных изображений. Можно обработать изображение в инструменте Wavelet 2-D, а затем сохранить обработанное изображение в MAT-файл (с расширением mat или другое).
Например, загрузите пример анализа:
Файл > Анализ примеров > Индексированные изображения > на уровне 3 с sym4 → Detail Durer
и выполните сжатие на оригинальное изображение. Когда вы закроете окно Wavelet 2-D Compression, обновите синтезированное изображение, нажав Да в появившемся диалоговом окне.
Затем из Вейвлета 2-D инструментов выберите Файл меню Изображения > Save > Synthesized опции. Появится диалоговое окно, позволяющее выбрать папку и имя файла для MAT-файла (с расширением mat или другое). В данном примере выберите имя symage.
Чтобы загрузить изображение в рабочую область, введите
load symage whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
X | 359x371 | 1065512 | double array |
map | 64x3 | 1536 | double array |
valTHR | 1x1 | 8 | double array |
wname | 1x4 | 8 | char array |
Синтезированное изображение определяется X и map содержит палитру. В сложение параметры шумоподавления или процесса сжатия задаются именем вейвлета (wname) и глобальный порог (valTHR).
Сохранение дискретных коэффициентов преобразования Вейвлета. Инструмент Вейвлета 2-D позволяет сохранить коэффициенты дискретного вейвлета преобразования (DWT) на диск. Тулбокс создает MAT-файл в текущей папке с выбранным именем.
Чтобы сохранить коэффициенты DWT из настоящего анализа, используйте опцию меню Файл > Сохранить > Коэффициенты.
Появляется диалоговое окно, которое позволяет вам задать папку и имя файла для хранения коэффициентов.
Рассмотрим пример анализа:
Файл > Анализ примеров > Индексированные изображения > на уровне 3 с sym4 → Detail Durer
После сохранения дискретных коэффициентов вейвлета в файл cfsdurer.mat, загрузите переменные в рабочую область:
load cfsdurer whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x142299 | 1138392 | double array |
map | 64x3 | 1536 | double array |
sizes | 5x2 | 80 | double array |
valTHR | 0x0 | 0 | double array |
wname | 1x4 | 8 | char array |
Переменные map содержит палитру. Переменные wname содержит имя вейвлета и valTHR пуст, поскольку синтезированное изображение совпадает с исходным.
Переменные coefs и sizes содержат дискретные коэффициенты вейвлета и связанные с ними размеры матрицы. Точнее, в приведенном выше примере, coefs является вектором 1 на 142299 конкатенированных коэффициентов и sizes задает длину каждого компонента.
Сохранение декомпозиций. Инструмент Вейвлета 2-D позволяет сохранить весь набор данных из дискретного вейвлета анализа на диск. Тулбокс создает MAT-файл в текущей папке с выбранным именем и расширением wa2 (вейвлет 2-D).
Откройте инструмент Wavelet 2-D и загрузите пример анализа:
Файл > Анализ примера > Индексированные изображения > на уровне 3 с sym4 → Detail Durer.
Чтобы сохранить данные этого анализа, используйте опцию меню Файл > Сохранить > Разложение.
Появляется диалоговое окно, которое позволяет вам задать папку и имя файла для хранения данных разложения. Введите имя decdurer.
После сохранения данных о разложении в файл decdurer.wa2, загрузите переменные в рабочую область:
load decdurer.wa2 -mat whos
| Имя | Размер | Байты | Класс |
|---|---|---|---|
coefs | 1x142299 | 1138392 | double array |
data_name | 1x6 | 12 | char array |
map | 64x3 | 1536 | double array |
sizes | 5x2 | 80 | double array |
valTHR | 0x0 | 0 | double array |
wave_name | 1x4 | 8 | char array |
Переменные coefs и sizes содержат структуру вейвлета разложения. Другие переменные содержат имя вейвлета, палитру и имя файла, содержащее данные. Переменные valTHR пуст, поскольку синтезированное изображение совпадает с исходным.
Примечание
Опции сохранения также доступны при выполнении шумоподавления или сжатия внутри инструмента Wavelet 2-D. В окне Wavelet 2-D Шумоподавление можно сохранить деноизированное изображение и разложение. То же самое относится и к окну Wavelet 2-D Compression. Таким образом, вы можете сохранить множество различных испытаний из окон Denoising и Compression, не возвращаясь к основному окну Wavelet 2-D в процессе настройки. При сохранении синтезированного сигнала, разложения или коэффициентов в MAT-файл, mat расширение файла не требуется. Можно сохранять приближения индивидуально для каждого уровня или сохранять все сразу.
Можно загрузить изображения, коэффициенты или разложения в приложение Wavelet Analyzer. Загружаемая информация могла быть ранее экспортирована из приложения Wavelet Analyzer, а затем манипулирована в рабочей области; или это может быть информация, сгенерированная вами первоначально из командной строки.
В любом случае необходимо наблюдать строгие форматы файлов и структуры данных, используемые инструментом Wavelet 2-D, иначе при попытке загрузить информацию возникнут ошибки.
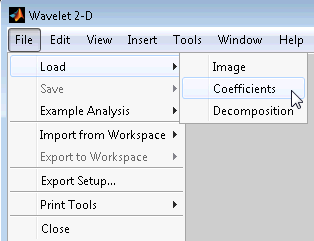
Загрузка изображений. Этот тулбокс поддерживает только индексированные изображения. Индексированное изображение является матрицей, содержащей только целые числа от 1 до n, где n количество цветов в изображении.
Это изображение может опционально сопровождаться n-by-3 матрица вызываемая map. Это палитра, связанная с изображением. Когда MATLAB отображает такое изображение, он использует значения матрицы, чтобы посмотреть нужный цвет в этой палитре. Если палитра не задана, инструмент Wavelet 2-D использует монотонную палитру с max(max(X))min(min(X))+1 цвета.
Чтобы загрузить изображение, созданное вами в рабочем пространстве MATLAB, в инструмент Wavelet 2-D, сохраните изображение (и, опционально, переменную map) в MAT-файле (с расширением mat или другое).
Для образца предположим, что вы создали изображение под названием мозг и хотите проанализировать его в Вейвлет 2-D инструменте. Напечатать
X = brain; map = pink(256); save myfile X map
Чтобы загрузить это изображение в инструмент Вейвлета 2-D, используйте меню опции Файла > Загрузка > Изображение.
Появится диалоговое окно, в котором можно выбрать подходящий MAT-файл для загрузки.
Примечание
Графические инструменты позволяют загружать изображение, которое не содержит целых чисел от 1 до n. Расчеты верны, потому что они действуют непосредственно на матрице, но отображение изображения странно. Значения меньше 1 оцениваются как 1, значения больше n оцениваются как n, а действительное значение в интервале [1, n] оценивается как ближайшее целое число.
Коэффициенты, приближения и детали, произведенные разложением вейвлетов, не являются индексированными матрицами изображений.
Чтобы отобразить эти изображения подходящим образом, инструмент Wavelet 2-D соблюдает эти правила:
Восстановленные приближения отображаются с помощью палитры map.
Коэффициенты и восстановленные детали отображаются с помощью палитры map применяется к измененной версии матриц.
Примечание
Первая переменная 2-D, встречающаяся в файле (кроме переменной map, который зарезервирован для палитры) считается изображением. Переменные проверяются в алфавитном порядке.
Загрузка коэффициентов дискретного Вейвлета преобразования. Чтобы загрузить дискретные коэффициенты преобразования вейвлета (DWT) в инструмент Вейвлета 2-D, сначала сохраните соответствующие данные в MAT-файле, который должен содержать по крайней мере две переменные:
coefs, вектор коэффициентов
sizes, матрица бухгалтерии
Для индексированного изображения матрица sizes является n+2массив -by-2:
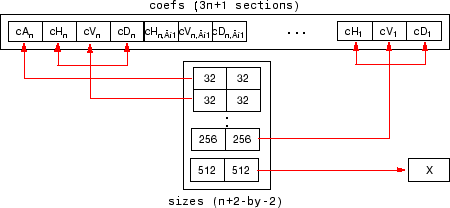
Для изображения truecolor матрица sizes является n+2-by-3:
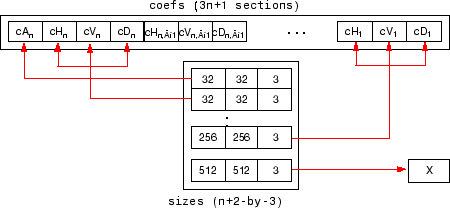
Переменные coefs должен быть вектором конкатенированных коэффициентов DWT. The coefs вектор для n-уровневое разложение содержит 3n+1 секции, состоящие из n уровня приближения, за которыми следуют горизонтальные, вертикальные и диагональные коэффициенты детализации в этом порядке для каждого уровня. Переменные sizes является матрицей, строки которой задают размер cAn, размер cHn (или cVn, или cDn),..., размером с cH1 (или cV1, или cD1) и размер оригинального изображения X. Размеры вертикальных и диагональных деталей совпадают с размерами горизонтальных деталей.
После построения или редактирования соответствующих данных в рабочем пространстве введите
save myfile coefs sizes
Используйте меню Файла > Загрузка > Коэффициенты опции из инструмента Вейвлета 2-D, чтобы загрузить данные в графический инструмент.
Появится диалоговое окно, позволяющее выбрать папку и файл, в которых находятся ваши данные.
Загрузка декомпозиций. Чтобы загрузить данные разложения дискретного вейвлет в инструмент Wavelet 2-D, необходимо сначала сохранить соответствующие данные в MAT-файле (с расширением wa2 или другое).
MAT-файл содержит эти переменные.
| Переменная | Статус | Описание |
|---|---|---|
coefs | Необходимый | Вектор конкатенированных коэффициентов DWT |
sizes | Необходимый | Матрица, задающая размеры компонентов |
wave_name | Необходимый | Вектор символов, задающий имя вейвлета, используемого для разложения (например |
map | Дополнительный |
|
data_name | Дополнительный | Вектор символов, задающий имя разложения |
После построения или редактирования соответствующих данных в рабочем пространстве введите
save myfile.wa2 coefs sizes wave_name
Используйте меню Файла > Загрузка > Разложение опции из инструмента Вейвлета 2-D, чтобы загрузить данные разложения изображения.
Появится диалоговое окно, позволяющее выбрать папку и файл, в которых находятся ваши данные.
Примечание
При загрузке изображения, разложения или коэффициентов из MAT-файла расширение этого файла свободно. The mat расширение не обязательно.