Симуляция Монте-Карло коррелированого актива возвращается
RetSeries = portsim(ExpReturn,ExpCovariance,NumObs)NASSETS активы по NUMOBS последовательные интервалы наблюдения. Возвраты актива симулированы как пропорциональный шаг постоянного дрейфа, постоянных стохастических процессов энергозависимости, таким образом, аппроксимировав геометрическое броуновское движение непрерывного времени.
RetSeries = portsim(___,RetIntervals,NumSim,Method)
Этот пример показывает различие между Exact и Expected методы симуляции.
Рассмотрите портфель пяти активов со следующими ожидаемыми доходами, стандартными отклонениями, и корреляционная матрица на основе ежедневного актива возвращается (где ExpReturn и Sigmas разделены на 100, чтобы преобразовать проценты в возвраты).
ExpReturn = [0.0246 0.0189 0.0273 0.0141 0.0311]/100;
Sigmas = [0.9509 1.4259 1.5227 1.1062 1.0877]/100;
Correlations = [1.0000 0.4403 0.4735 0.4334 0.6855
0.4403 1.0000 0.7597 0.7809 0.4343
0.4735 0.7597 1.0000 0.6978 0.4926
0.4334 0.7809 0.6978 1.0000 0.4289
0.6855 0.4343 0.4926 0.4289 1.0000];Преобразуйте корреляции и стандартные отклонения к ковариационной матрице.
ExpCovariance = corr2cov(Sigmas, Correlations)
ExpCovariance = 5×5
10-3 ×
0.0904 0.0597 0.0686 0.0456 0.0709
0.0597 0.2033 0.1649 0.1232 0.0674
0.0686 0.1649 0.2319 0.1175 0.0816
0.0456 0.1232 0.1175 0.1224 0.0516
0.0709 0.0674 0.0816 0.0516 0.1183
Примите, что существует 252 торговых дня в календарный год и симулируют два демонстрационных пути (реализация) ежедневной газеты, возвращает более чем период 2D года. Начиная с ExpReturn и ExpCovariance ежедневно описываются, установите RetIntervals = 1.
StartPrice = 100; NumObs = 504; % two calendar years of daily returns NumSim = 2; RetIntervals = 1; % one trading day NumAssets = 5;
Чтобы проиллюстрировать различие между методами, симулируйте два пути каждым методом, начиная с того же состояния случайных чисел.
rng('default'); RetExact = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Exact'); rng(0); RetExpected = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Expected');
Сравните среднее значение и ковариацию RetExact с входными параметрами (ExpReturn и ExpCovariance), вы заметите, что они почти идентичны.
На данном этапе RetExact и RetExpected оба 504 5 2 массивами. Теперь примите одинаково взвешенный портфель, сформированный из этих пяти активов, и создайте массивы портфеля, возвращается, в котором каждый столбец представляет портфель, возвращаются из соответствующего демонстрационного пути симулированных возвратов этих пяти активов. Массивы портфеля PortRetExact и PortRetExpected 504 2 матрицы.
Weights = ones(NumAssets, 1)/NumAssets; PortRetExact = zeros(NumObs, NumSim); PortRetExpected = zeros(NumObs, NumSim); for i = 1:NumSim PortRetExact(:,i) = RetExact(:,:,i) * Weights; PortRetExpected(:,i) = RetExpected(:,:,i) * Weights; end
Наконец, преобразуйте симулированный портфель, возвращается к ценам, и отобразите данные на графике. В частности, обратите внимание что начиная с Exact ожидаемый доход соответствий метода и ковариация, терминальные цены портфеля фактически идентичны для каждого демонстрационного пути. Это не верно для Expected метод симуляции. Несмотря на то, что этот пример исследует портфели, те же методы применяются к отдельным активам также. Таким образом, Exact симуляция является самой соответствующей, когда уникальные пути обязаны достигать тех же терминальных цен.
PortExact = ret2tick(PortRetExact, ... repmat(StartPrice,1,NumSim)); PortExpected = ret2tick(PortRetExpected, ... repmat(StartPrice,1,NumSim)); subplot(2,1,1), plot(PortExact, '-r') ylabel('Portfolio Prices') title('Exact Method') subplot(2,1,2), plot(PortExpected, '-b') ylabel('Portfolio Prices') title('Expected Method')

ExpReturn, ExpCovariance, и RetIntervalsЭтот пример показывает взаимодействие среди ExpReturn, ExpCovariance, и RetIntervals. Вспомните тот portsim симулирует коррелируемый актив, возвращает на интервале длины dt, данный уравнением
где S является ценой активов, μ является ожидаемой нормой прибыли, σ является энергозависимостью цены активов, и ε представляет случайный рисунок от стандартизированного нормального распределения.
Шаг времени dt определяется дополнительным входом RetIntervals, или как явный входной параметр или как единица времени постепенно увеличиваются по умолчанию. Независимо, периодичность ExpReturn, ExpCovariance, и RetIntervals должно быть сопоставимым. Например, если ExpReturn и ExpCovariance пересчитаны на год, затем RetIntervals должен быть в годах. Эта точка часто неправильно понимается.
Проиллюстрировать взаимодействие среди ExpReturn, ExpCovariance, и RetIntervals, рассмотрите портфель пяти активов со следующими ожидаемыми доходами, стандартными отклонениями, и корреляционная матрица на основе ежедневного актива возвращается.
ExpReturn = [0.0246 0.0189 0.0273 0.0141 0.0311]/100;
Sigmas = [0.9509 1.4259 1.5227 1.1062 1.0877]/100;
Correlations = [1.0000 0.4403 0.4735 0.4334 0.6855
0.4403 1.0000 0.7597 0.7809 0.4343
0.4735 0.7597 1.0000 0.6978 0.4926
0.4334 0.7809 0.6978 1.0000 0.4289
0.6855 0.4343 0.4926 0.4289 1.0000];
Преобразуйте корреляции, и стандартные отклонения к ковариационной матрице ежедневной газеты возвращается.
ExpCovariance = corr2cov(Sigmas, Correlations);
Примите 252 торговых дня в календарный год и симулируйте один демонстрационный путь ежедневной газеты, возвращается за четырехлетний период. Начиная с ExpReturn и ExpCovariance входные параметры ежедневно описываются, установите RetIntervals = 1.
StartPrice = 100; NumObs = 1008; % four calendar years of daily returns RetIntervals = 1; % one trading day NumAssets = length(ExpReturn); randn('state',0); RetSeries1 = portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, 1, 'Expected');
Теперь пересчитайте на год ежедневные данные, таким образом, изменив периодичность данных, путем умножения ExpReturn и ExpCovariance 252 и делящийся RetIntervals 252 (RetIntervals = 1/252 года). Сбрасывая генератор случайных чисел к его начальному состоянию, можно воспроизвести результаты.
rng('default'); RetSeries2 = portsim(ExpReturn*252, ExpCovariance*252, ... NumObs, RetIntervals/252, 1, 'Expected');
Примите одинаково взвешенный портфель и вычислите портфель, возвращается сопоставленный с каждым симулированным, возвращают ряд.
Weights = ones(NumAssets, 1)/NumAssets; PortRet1 = RetSeries2 * Weights; PortRet2 = RetSeries2 * Weights;
Сравнение данных показывает тот PortRet1 и PortRet2 идентичны.
В этом примере показано, как симулировать одномерный процесс геометрического броуновского движения. Это основано на примере, найденном в Оболочке, Опциях, фьючерсах и Других Производных, 5-й Выпуск (см. пример 12.2 на странице 236). В дополнение к проверке примера Оболочки это также графически иллюстрирует логарифмически нормальное свойство терминальных курсов акций довольно большой симуляцией Монте-Карло.
Примите, что вы владеете запасом с начальной ценой 20$, пересчитанным на год ожидаемым доходом 20% и энергозависимостью 40%. Симулируйте ежедневный ценовой процесс для этого запаса в течение одного целого календарного года (252 торговых дня).
StartPrice = 20; ExpReturn = 0.2; ExpCovariance = 0.4^2; NumObs = 252; NumSim = 10000; RetIntervals = 1/252;
RetIntervals описывается в годах, сопоставимых с фактом что ExpReturn и ExpCovariance пересчитаны на год. Кроме того, ExpCovariance вводится как отклонение, а не более знакомое стандартное отклонение (энергозависимость).
Установите состояние генератора случайных чисел и симулируйте 10 000 испытаний (реализация) запаса, возвращается за целый календарный год 252 торговых дней.
rng('default'); RetSeries = squeeze(portsim(ExpReturn, ExpCovariance, NumObs, ... RetIntervals, NumSim, 'Expected'));
squeeze функция переформатировала выходной массив симулированных возвратов из 252- 1- 10000 массив к более удобному 252- 10000 массив. (Вспомните тот portsim существенно многомерный механизм симуляции).
В соответствии с уравнениями 12.4 и 12.5 Оболочки на странице 236
преобразуйте симулированный ряд возврата в ценовой ряд и вычислите демонстрационное среднее значение и отклонение терминальных курсов акций.
StockPrices = ret2tick(RetSeries, repmat(StartPrice, 1, NumSim)); SampMean = mean(StockPrices(end,:)) SampVar = var(StockPrices(end,:))
SampMean = 24.4489 SampVar = 101.4243
Сравните эти значения со значениями, которые вы получаете при помощи уравнений Оболочки.
ExpValue = StartPrice*exp(ExpReturn) ExpVar = ... StartPrice*StartPrice*exp(2*ExpReturn)*(exp((ExpCovariance)) - 1)
ExpValue = 24.4281 ExpVar = 103.5391
Эти результаты очень близко к результатам, показанным в примере Оболочки 12.2.
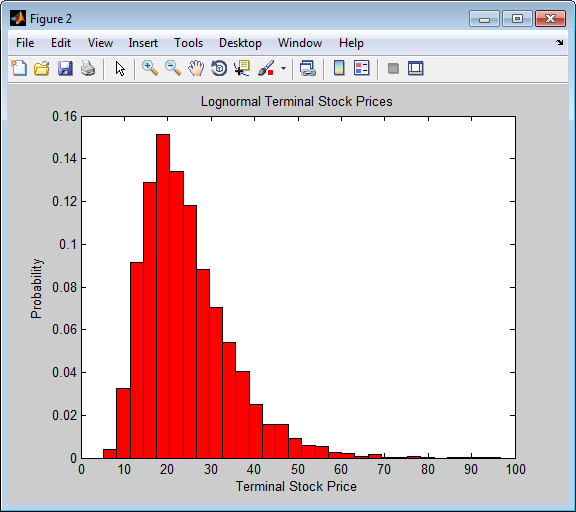
Отобразите демонстрационную функцию плотности терминального курса акций после одного календарного года. От демонстрационной функции плотности логарифмически нормальное распределение терминальных курсов акций очевидно.
[count, BinCenter] = hist(StockPrices(end,:), 30); figure bar(BinCenter, count/sum(count), 1, 'r') xlabel('Terminal Stock Price') ylabel('Probability') title('Lognormal Terminal Stock Prices')
ExpReturn — Ожидаемый (средний) возврат каждого активаОжидаемый (средний) возврат каждого актива в виде 1- NASSETS вектор.
Типы данных: double
ExpCovariance — Актив возвращает ковариацииАктив возвращает ковариации в виде NASSETS- NASSETS матрица. ExpCovariance должно быть симметричным и положительный полуопределенный (никакие отрицательные собственные значения). Стандартными отклонениями возвратов является ExpSigma = sqrt(diag(ExpCovariance)). Если ExpCovariance не симметричная положительная полуопределенная матрица, использовать nearcorr создать положительную полуопределенную матрицу для корреляционной матрицы.
Типы данных: double
NumObs — Количество последовательных наблюдений во временных рядах возвратаколичество последовательных наблюдений во временных рядах возврата в виде положительного скалярного целого числа. Если NumObs вводится как пустой матричный [], длина RetIntervals используется.
Типы данных: double
RetIntervals — Времена интервала между наблюдениями(Необязательно) времена Интервала между наблюдениями в виде положительной скалярной величины или многими наблюдениями NUMOBS- 1 вектор. Если RetIntervals не задан, все интервалы приняты, чтобы иметь длину 1.
Типы данных: double
NumSim — Количество симулированных демонстрационных путей (реализация) NUMOBS наблюдения(Необязательно) Количество симулированных демонстрационных путей (реализация) NUMOBS наблюдения в виде положительного скалярного целого числа. Значение по умолчанию для NumSim 1 (одна реализация NUMOBS коррелированый актив возвращается).
Типы данных: double
Method — Тип симуляции Монте-Карло'Exact' (значение по умолчанию) | вектор символов(Необязательно) Тип симуляции Монте-Карло в виде вектора символов с одним из следующих значений:
'Exact' (значение по умолчанию) генерирует коррелируемый актив, возвращается, в котором демонстрационное среднее значение и ковариация совпадают с входным средним значением (ExpReturn) и ковариация (ExpCovariance) технические требования.
'Expected' генерирует коррелируемый актив, возвращается, в котором демонстрационное среднее значение и ковариация статистически равны входному среднему значению и техническим требованиям ковариации. (Ожидаемые значения демонстрационного среднего значения и ковариации равны входному среднему значению (ExpReturn) и ковариация (ExpCovariance) технические требования.)
Для любого Method, демонстрационное среднее значение и возвращенная ковариация соответственно масштабируются RetIntervals.
Типы данных: char
RetSeries — 3D массив коррелированого, нормально распределенного, пропорционального актива возвращается3D массив коррелированого, нормально распределенного, пропорционального актива возвращается, возвращенный как NUMOBS- NASSETS- NUMSIM 3D массив.
Актив возвращается на интервале длины, которой дан dt
где S является ценой активов, μ является ожидаемой нормой прибыли, σ является энергозависимостью цены активов, и ε представляет случайный рисунок от стандартизированного нормального распределения.
Примечания
Когда Method 'Exact', демонстрационное среднее значение и ковариация всей реализации (масштабируемый RetIntervals) совпадайте с входным средним значением и ковариацией. Когда возвраты затем преобразованы в цены активов, все терминальные цены на данный актив находятся в близком соглашении. Несмотря на то, что вся реализация чертится независимо, они производят подобные терминальные цены активов. Установите Method к 'Expected' избегать этого поведения.
Возвраты из портфелей в PortWts даны PortReturn = PortWts * RetSeries(:,:,1)', где PortWts матрица, в которой каждая строка содержит распределение активов портфеля. Каждая строка PortReturn соответствует одному из портфелей, идентифицированных в PortWts, и каждый столбец соответствует одному из наблюдений, взятых из первой реализации (первая плоскость) в RetSeries. Смотрите portopt и portstats для спецификации портфеля и оптимизации.
[1] Оболочка, J. C. Опции, фьючерсы и другие производные. Prentice Hall, 2003.
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.