Постройте решение или mesh для 2D проблемы
pdeplot( строит решение model,'XYData',results.NodalSolution)model в узловых местоположениях как цветная объемная поверхностная диаграмма с помощью 'jet' по умолчанию палитра.
pdeplot( строит температуру в узловых местоположениях для 2D тепловой аналитической модели. Этот синтаксис создает цветную объемную поверхностную диаграмму с помощью model,'XYData',results.Temperature,'ColorMap','hot')'hot' палитра.
pdeplot( строит напряжение фон Мизеса и показывает деформированную форму для 2D модели структурного анализа.model,'XYData',results.VonMisesStress,'Deformation',results.Displacement)
pdeplot( строит model,'XYData',results.ModeShapes.ux)x- компонент модального смещения для 2D структурной модальной аналитической модели.
pdeplot(___, строит mesh, данные в узловых местоположениях, или и mesh и данные, в зависимости от Name,Value)Name,Value парные аргументы. Используйте любые аргументы от предыдущих синтаксисов.
Задайте по крайней мере один из FlowData (векторный полевой график), XYData (окрашенный объемной поверхностной диаграммой), или ZData (3-D график высоты) пары "имя-значение". В противном случае, pdeplot строит mesh без данных. Можно объединить любое количество типов графика.
Для тепловой модели можно построить температуру или градиент температуры.
Для структурной модели можно построить смещение, напряжение, деформацию и напряжение фон Мизеса. Кроме того, можно показать деформированную форму и задать масштабный коэффициент для графика деформации.
Создайте модель PDE. Включайте геометрию встроенной функции lshapeg. Поймайте в сети геометрию и постройте ее.
model = createpde; geometryFromEdges(model,@lshapeg); mesh = generateMesh(model); pdeplot(model)

В качестве альтернативы можно построить mesh при помощи mesh как входной параметр.
pdeplot(mesh)

Другой подход должен использовать узлы и элементы mesh как входные параметры для pdeplot.
pdeplot(mesh.Nodes,mesh.Elements)

Отобразите метки узла. Используйте xlim и ylim увеличить масштаб конкретных узлов.
pdeplot(model,'NodeLabels','on') xlim([-0.2,0.2]) ylim([-0.2,0.2])

Отобразите метки элемента.
pdeplot(model,'ElementLabels','on') xlim([-0.2,0.2]) ylim([-0.2,0.2])

Создайте окрашенные 2D и 3-D графики решения модели PDE.
Создайте модель PDE. Включайте геометрию встроенной функции lshapeg. Поймайте в сети геометрию.
model = createpde; geometryFromEdges(model,@lshapeg); generateMesh(model);
Установите нуль граничные условия Дирихле на всех ребрах.
applyBoundaryCondition(model,'dirichlet', ... 'Edge',1:model.Geometry.NumEdges, ... 'u',0);
Задайте коэффициенты и решите УЧП.
specifyCoefficients(model,'m',0, ... 'd',0, ... 'c',1, ... 'a',0, ... 'f',1); results = solvepde(model)
results =
StationaryResults with properties:
NodalSolution: [1177x1 double]
XGradients: [1177x1 double]
YGradients: [1177x1 double]
ZGradients: []
Mesh: [1x1 FEMesh]
Доступ к решению в узловых местоположениях.
u = results.NodalSolution;
Постройте 2D решение.
pdeplot(model,'XYData',u)
Постройте 3-D решение.
pdeplot(model,'XYData',u,'ZData',u)

Постройте градиент решения для УЧП как график полей градиента.
Создайте модель PDE. Включайте геометрию встроенной функции lshapeg. Поймайте в сети геометрию.
model = createpde; geometryFromEdges(model,@lshapeg); generateMesh(model);
Установите нуль граничные условия Дирихле на всех ребрах.
applyBoundaryCondition(model,'dirichlet', ... 'Edge',1:model.Geometry.NumEdges, ... 'u',0);
Задайте коэффициенты и решите УЧП.
specifyCoefficients(model,'m',0, ... 'd',0, ... 'c',1, ... 'a',0, ... 'f',1); results = solvepde(model)
results =
StationaryResults with properties:
NodalSolution: [1177x1 double]
XGradients: [1177x1 double]
YGradients: [1177x1 double]
ZGradients: []
Mesh: [1x1 FEMesh]
Доступ к градиенту решения в узловых местоположениях.
ux = results.XGradients; uy = results.YGradients;
Постройте градиент как график полей градиента.
pdeplot(model,'FlowData',[ux,uy])
Постройте решение 2D УЧП в 3-D с 'jet' окраска и mesh, и включает график полей градиента. Получите указатели на объекты осей.
Создайте модель PDE. Включайте геометрию встроенной функции lshapeg. Поймайте в сети геометрию.
model = createpde; geometryFromEdges(model,@lshapeg); generateMesh(model);
Установите нуль граничные условия Дирихле на всех ребрах.
applyBoundaryCondition(model,'dirichlet', ... 'Edge',1:model.Geometry.NumEdges, ... 'u',0);
Задайте коэффициенты и решите УЧП.
specifyCoefficients(model,'m',0, ... 'd',0, ... 'c',1, ... 'a',0, ... 'f',1); results = solvepde(model)
results =
StationaryResults with properties:
NodalSolution: [1177x1 double]
XGradients: [1177x1 double]
YGradients: [1177x1 double]
ZGradients: []
Mesh: [1x1 FEMesh]
Доступ к решению и его градиенту в узловых местоположениях.
u = results.NodalSolution; ux = results.XGradients; uy = results.YGradients;
Постройте решение в 3-D с 'jet' окраска и mesh, и включает градиент как график полей градиента.
h = pdeplot(model,'XYData',u,'ZData',u, ... 'FaceAlpha',0.5, ... 'FlowData',[ux,uy], ... 'ColorMap','jet', ... 'Mesh','on')

h = 3x1 graphics array: Patch Quiver ColorBar
Решите 2D переходную тепловую задачу.
Создайте переходную тепловую модель для этой проблемы.
thermalmodel = createpde('thermal','transient');
Создайте геометрию и включайте ее в модель.
SQ1 = [3; 4; 0; 3; 3; 0; 0; 0; 3; 3]; D1 = [2; 4; 0.5; 1.5; 2.5; 1.5; 1.5; 0.5; 1.5; 2.5]; gd = [SQ1 D1]; sf = 'SQ1+D1'; ns = char('SQ1','D1'); ns = ns'; dl = decsg(gd,sf,ns); geometryFromEdges(thermalmodel,dl); pdegplot(thermalmodel,'EdgeLabels','on','FaceLabels','on') xlim([-1.5 4.5]) ylim([-0.5 3.5]) axis equal

Для квадратной области присвойте эти тепловые свойства:
Теплопроводность
Массовая плотность
Удельная теплоемкость
thermalProperties(thermalmodel,'ThermalConductivity',10, ... 'MassDensity',2, ... 'SpecificHeat',0.1, ... 'Face',1);
Для ромбовидной области присвойте эти тепловые свойства:
Теплопроводность
Массовая плотность
Удельная теплоемкость
thermalProperties(thermalmodel,'ThermalConductivity',2, ... 'MassDensity',1, ... 'SpecificHeat',0.1, ... 'Face',2);
Примите, что ромбовидная область является источником тепла с плотностью .
internalHeatSource(thermalmodel,4,'Face',2);Примените постоянную температуру сторонам квадратной пластины.
thermalBC(thermalmodel,'Temperature',0,'Edge',[1 2 7 8]);
Установите начальную температуру на 0 °C.
thermalIC(thermalmodel,0);
Сгенерируйте mesh.
generateMesh(thermalmodel);
Движущие силы для этой проблемы очень быстры. Температура достигает устойчивого состояния приблизительно за 0,1 секунды. Чтобы получить интересную часть динамики, установите время решения на logspace(-2,-1,10). Эта команда возвращается 10 логарифмически расположенных с интервалами раз решения между 0,01 и 0.1.
tlist = logspace(-2,-1,10);
Решите уравнение.
thermalresults = solve(thermalmodel,tlist);
Постройте решение с изотермическими линиями при помощи контурного графика.
T = thermalresults.Temperature; pdeplot(thermalmodel,'XYData',T(:,10),'Contour','on','ColorMap','hot')

Создайте модель структурного анализа для статической проблемы плоской деформации.
structuralmodel = createpde('structural','static-planestrain');
Создайте геометрию и включайте ее в модель. Постройте геометрию.
geometryFromEdges(structuralmodel,@squareg); pdegplot(structuralmodel,'EdgeLabels','on') axis equal

Задайте модуль Молодежи и отношение Пуассона.
structuralProperties(structuralmodel,'PoissonsRatio',0.3, ... 'YoungsModulus',210E3);
Задайте x-компонент вынужденного смещения для ребра 1.
structuralBC(structuralmodel,'XDisplacement',0.001,'Edge',1);
Укажите, что ребро 3 является фиксированным контуром.
structuralBC(structuralmodel,'Constraint','fixed','Edge',3);
Сгенерируйте mesh и решите задачу.
generateMesh(structuralmodel); structuralresults = solve(structuralmodel);
Постройте деформированную форму с помощью масштабного коэффициента по умолчанию. По умолчанию, pdeplot внутренне определяет масштабный коэффициент на основе размерностей геометрии и величины деформации.
pdeplot(structuralmodel, ... 'XYData',structuralresults.VonMisesStress, ... 'Deformation',structuralresults.Displacement, ... 'ColorMap','jet')

Постройте деформированную форму с масштабным коэффициентом 500.
pdeplot(structuralmodel, ... 'XYData',structuralresults.VonMisesStress, ... 'Deformation',structuralresults.Displacement, ... 'DeformationScaleFactor',500,... 'ColorMap','jet')

Постройте деформированную форму без масштабирования.
pdeplot(structuralmodel,'XYData',structuralresults.VonMisesStress, ... 'ColorMap','jet')

Найдите основной (самый низкий) режим 2D консольного луча, приняв распространенность условия плоского напряжения.
Задайте следующие геометрические и структурные свойства луча, наряду с модульной толщиной плоского напряжения.
length = 5; height = 0.1; E = 3E7; nu = 0.3; rho = 0.3/386;
Создайте модель плоского напряжения модели, присвойте геометрию и сгенерируйте mesh.
structuralmodel = createpde('structural','modal-planestress'); gdm = [3;4;0;length;length;0;0;0;height;height]; g = decsg(gdm,'S1',('S1')'); geometryFromEdges(structuralmodel,g);
Задайте максимальный размер элемента (пять элементов через толщину луча).
hmax = height/5;
msh=generateMesh(structuralmodel,'Hmax',hmax);Задайте структурные свойства и граничные ограничения.
structuralProperties(structuralmodel,'YoungsModulus',E, ... 'MassDensity',rho, ... 'PoissonsRatio',nu); structuralBC(structuralmodel,'Edge',4,'Constraint','fixed');
Вычислите аналитическую основную частоту (Гц) с помощью теории луча.
I = height^3/12; analyticalOmega1 = 3.516*sqrt(E*I/(length^4*(rho*height)))/(2*pi)
analyticalOmega1 = 126.9498
Задайте частотный диапазон, который включает аналитически вычисленную частоту, и решите модель.
modalresults = solve(structuralmodel,'FrequencyRange',[0,1e6])modalresults =
ModalStructuralResults with properties:
NaturalFrequencies: [32x1 double]
ModeShapes: [1x1 FEStruct]
Mesh: [1x1 FEMesh]
Решатель находит собственные частоты и модальные значения смещения в узловых местоположениях. Чтобы получить доступ к этим значениям, используйте modalresults.NaturalFrequencies и modalresults.ModeShapes.
modalresults.NaturalFrequencies/(2*pi)
ans = 32×1
105 ×
0.0013
0.0079
0.0222
0.0433
0.0711
0.0983
0.1055
0.1462
0.1930
0.2455
⋮
modalresults.ModeShapes
ans =
FEStruct with properties:
ux: [6511x32 double]
uy: [6511x32 double]
Magnitude: [6511x32 double]
Постройте y-компонент решения для основной частоты.
pdeplot(structuralmodel,'XYData',modalresults.ModeShapes.uy(:,1)) title(['First Mode with Frequency ', ... num2str(modalresults.NaturalFrequencies(1)/(2*pi)),' Hz']) axis equal

Решите электромагнитную задачу и найдите электрический потенциал и полевое распределение для 2D геометрии, представляющей пластину отверстием.
Создайте электромагнитную модель для электростатического анализа.
emagmodel = createpde('electromagnetic','electrostatic');
Импортируйте и постройте геометрию, представляющую пластину отверстием.
importGeometry(emagmodel,'PlateHolePlanar.stl'); pdegplot(emagmodel,'EdgeLabels','on')

Задайте вакуумную проницаемость в системе СИ модулей.
emagmodel.VacuumPermittivity = 8.8541878128E-12;
Задайте относительную проницаемость материала.
electromagneticProperties(emagmodel,'RelativePermittivity',1);Примените граничные условия напряжения на ребра, структурирующие прямоугольник и круг.
electromagneticBC(emagmodel,'Voltage',0,'Edge',1:4); electromagneticBC(emagmodel,'Voltage',1000,'Edge',5);
Задайте плотность заряда для целой геометрии.
electromagneticSource(emagmodel,'ChargeDensity',5E-9);Сгенерируйте mesh.
generateMesh(emagmodel);
Решите модель.
R = solve(emagmodel)
R =
ElectrostaticResults with properties:
ElectricPotential: [1218x1 double]
ElectricField: [1x1 FEStruct]
ElectricFluxDensity: [1x1 FEStruct]
Mesh: [1x1 FEMesh]
Постройте электрический потенциал и поле.
pdeplot(emagmodel,'XYData',R.ElectricPotential, ... 'FlowData',[R.ElectricField.Ex ... R.ElectricField.Ey]) axis equal

Постройте p,e,t mesh. Отобразите решение с помощью 2D и 3-D цветных графиков.
Создайте геометрию, mesh, граничные условия, коэффициенты УЧП и решение.
[p,e,t] = initmesh('lshapeg'); u = assempde('lshapeb',p,e,t,1,0,1);
Постройте mesh.
pdeplot(p,e,t)

Постройте решение как 2D цветной график.
pdeplot(p,e,t,'XYData',u)
Постройте решение как 3-D цветной график.
pdeplot(p,e,t,'XYData',u,'ZData',u)

model — Объект моделиPDEModel возразите | ThermalModel возразите | StructuralModel возразите | ElectromagneticModel объектОбъект модели в виде PDEModel объект, ThermalModel объект, StructuralModel объект или ElectromagneticModel объект.
Пример: model = createpde(1)
Пример: thermalmodel = createpde('thermal','steadystate')
Пример: structuralmodel = createpde('structural','static-solid')
Пример: emagmodel = createpde('electromagnetic','magnetostatic')
mesh — Объект ячейкиMesh свойство PDEModel возразите | выход generateMeshОбъект ячейки в виде Mesh свойство PDEModel возразите или как выход generateMesh.
Пример: model.Mesh
nodes — Узловые координатыУзловые координаты в виде 2 NumNodes матрицей. NumNodes является количеством узлов.
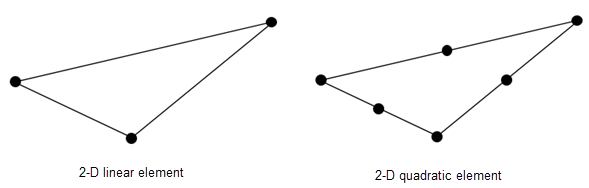
elements — Матрица смежности элемента в терминах идентификаторов узлаМатрица смежности элемента в терминах идентификаторов узла в виде 3 NumElements или 6 NumElements матрицей. Линейные сетки содержат только угловые узлы. Для линейных сеток матрица смежности имеет три узла на 2D элемент. Квадратичные сетки содержат угловые узлы и узлы посреди каждого ребра элемента. Для квадратичных сеток матрица смежности имеет шесть узлов на 2D элемент.
p — Поймайте в сети точкиПоймайте в сети точки в виде 2 Np матрица точек, где Np число точек в mesh. Для описания (pET) матрицы, смотрите Данные о Mesh, когда [p, e, t] Утраивается.
Как правило, вы используете pE, и t данные, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
e — Поймайте в сети ребраПоймайте в сети ребра в виде 7- Ne матрица ребер, где Ne количество ребер в mesh. Для описания (pET) матрицы, смотрите Данные о Mesh, когда [p, e, t] Утраивается.
Как правило, вы используете pE, и t данные, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
t — Поймайте в сети треугольникиПоймайте в сети треугольники в виде 4- Nt матрица треугольников, где Nt количество треугольников в mesh. Для описания (pET) матрицы, смотрите Данные о Mesh, когда [p, e, t] Утраивается.
Как правило, вы используете pE, и t данные, экспортированные из приложения PDE Modeler или сгенерированные initmesh или refinemesh.
Пример: [p,e,t] = initmesh(gd)
Типы данных: double
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
pdeplot(model,'XYData',u,'ZData',u)Когда вы используете PDEModel объект, pdeplot(model,'XYData',u,'ZData',u) объемная поверхностная диаграмма наборов, окрашивающая к решению u, и устанавливает высоты для 3-D графика к u. Здесь u NodalSolution свойство результатов УЧП возвращено solvepde или solvepdeeig.
Когда вы используете [p,e,t] представление, pdeplot(p,e,t,'XYData',u,'ZData',u) объемная поверхностная диаграмма наборов, окрашивающая к решению u и устанавливает высоты для 3-D графика к решению u. Здесь u решение, возвращенное устаревшим решателем, такой как assempde.
Совет
Задайте по крайней мере один из FlowData (векторный полевой график), XYData (окрашенный объемной поверхностной диаграммой), или ZData (3-D график высоты) пары "имя-значение". В противном случае, pdeplot строит mesh без данных.
XYData — Окрашенные данные об объемной поверхностной диаграммеОкрашенные данные об объемной поверхностной диаграмме в виде разделенной запятой пары, состоящей из 'XYData' и вектор. Если вы используете [p,e,t] представление, задайте данные для точек в векторе из длины size(p,2), или задайте данные для треугольников в векторе из длины size(t,2).
Как правило, вы устанавливаете XYData к решению u. pdeplot функционируйте использует XYData для окраски и 2D и 3-D графики.
pdeplot использует палитру, заданную в ColorMap пара "имя-значение", с помощью стиля задана в XYStyle пара "имя-значение".
Когда Contour парой "имя-значение" является 'on', pdeplot также кривые уровня графиков XYData.
pdeplot строит действительную часть комплексных данных.
Построить kкомпонент th решения системы УЧП, извлеките соответствующую часть решения. Например, при использовании PDEModel возразите, задайте:
results = solvepde(model); u = results.NodalSolution; % each column of u has one component of u pdeplot(model,'XYData',u(:,k)) % data for column k
При использовании [p,e,t] представление, задайте:
np = size(p,2); % number of node points uk = reshape(u,np,[]); % each uk column has one component of u pdeplot(p,e,t,'XYData',uk(:,k)) % data for column k
Пример: 'XYData',u
Типы данных: double
XYStyle — Окраска выбора'interp' (значение по умолчанию) | 'off' | 'flat'Окраска выбора в виде разделенной запятой пары, состоящей из 'XYStyle' и 'interp'off, или 'flat'.
'off' — Никакая штриховка, только сцепитесь, отображен.
'flat' — Каждый треугольник в mesh имеет единый цвет.
'interp' — Окраска графика гладко интерполирована.
Окрашивающий выбор относится к XYData пара "имя-значение".
Пример: 'XYStyle','flat'
Типы данных: char | string
ZData — Данные для 3-D высот графикаДанные для 3-D высот графика в виде разделенной запятой пары, состоящей из 'ZData' и матрица. Если вы используете [p,e,t] представление, обеспечьте данные для точек в векторе из длины size(p,2) или данные для треугольников в векторе из длины size(t,2).
Как правило, вы устанавливаете ZData к uРешение. XYData пара "имя-значение" устанавливает окраску 3-D графика.
ZStyle пара "имя-значение" задает, непрерывен ли график или прерывист.
pdeplot строит действительную часть комплексных данных.
Построить kкомпонент th решения системы УЧП, извлеките соответствующую часть решения. Например, при использовании PDEModel возразите, задайте:
results = solvepde(model); u = results.NodalSolution; % each column of u has one component of u pdeplot(model,'XYData',u(:,k),'ZData',u(:,k)) % data for column k
При использовании [p,e,t] представление, задайте:
np = size(p,2); % number of node points uk = reshape(u,np,[]); % each uk column has one component of u pdeplot(p,e,t,'XYData',uk(:,k),'ZData',uk(:,k)) % data for column k
Пример: 'ZData',u
Типы данных: double
ZStyle — 3-D стиль графика'continuous' (значение по умолчанию) | 'off' | 'discontinuous'3-D стиль графика в виде разделенной запятой пары, состоящей из 'ZStyle' и одно из этих значений:
'off' — Никакой 3-D график.
'discontinuous' — Каждый треугольник в mesh имеет универсальную высоту в 3-D графике.
'continuous' — 3-D объемная поверхностная диаграмма непрерывна.
Если вы используете ZStyle не задавая ZData пара "имя-значение", затем pdeplot игнорирует ZStyle.
Пример: 'ZStyle','discontinuous'
Типы данных: char | string
FlowData — Данные для графика полей градиентаДанные для графика полей градиента в виде разделенной запятой пары, состоящей из 'FlowData' и M- 2 матрица, где M количество узлов mesh. FlowData содержит x и значения y поля в точках mesh.
Когда вы используете PDEModel объект, набор FlowData можно следующим образом:
results = solvepde(model);
gradx = results.XGradients;
grady = results.YGradients;
pdeplot(model,'FlowData',[gradx grady])Когда вы используете [p,e,t] представление, набор FlowData можно следующим образом:
[gradx,grady] = pdegrad(p,t,u); % Calculate gradient pdeplot(p,e,t,'FlowData',[gradx;grady])
Когда вы используете ZData чтобы представлять 2D решение для УЧП как, 3-D график и вы также включаете график полей градиента, график полей градиента появляется в z = 0 плоскостей.
pdeplot строит действительную часть комплексных данных.
Пример: 'FlowData',[ux uy]
Типы данных: double
FlowStyle — Индикатор, чтобы показать график полей градиента'arrow' (значение по умолчанию) | 'off'Индикатор, чтобы показать график полей градиента в виде разделенной запятой пары, состоящей из 'FlowStyle' и 'arrow' или 'off'. Здесь, 'arrow' отображает график полей градиента, заданный FlowData пара "имя-значение".
Пример: 'FlowStyle','off'
Типы данных: char | string
XYGrid — Индикатор, чтобы преобразовать данные о mesh в x-y сетка'off' (значение по умолчанию) | 'on'Индикатор, чтобы преобразовать данные о mesh в x-y сетка прежде, чем построить в виде разделенной запятой пары, состоящей из 'XYGrid' и 'off' или 'on'.
Примечание
Это преобразование может изменить геометрию и уменьшить качество графика.
По умолчанию сетка имеет о sqrt(size(t,2)) элементы в каждом направлении.
Пример: 'XYGrid','on'
Типы данных: char | string
GridParam — Индивидуально настраиваемый x-y сетка[tn;a2;a3] от более раннего вызова до tri2gridИндивидуально настраиваемый x-y сетка в виде разделенной запятой пары, состоящей из 'GridParam' и матричный [tn;a2;a3]. Например:
[~,tn,a2,a3] = tri2grid(p,t,u,x,y); pdeplot(p,e,t,'XYGrid','on','GridParam',[tn;a2;a3],'XYData',u)
Для получения дополнительной информации на данных о сетке и его x и y аргументы, смотрите tri2grid. tri2grid функция не работает с PDEModel объекты.
Пример: 'GridParam',[tn;a2;a3]
Типы данных: double
NodeLabels — Метки узла'off' (значение по умолчанию) | 'on'Узел помечает в виде разделенной запятой пары, состоящей из 'NodeLabels' и 'off' или 'on'.
pdeplot игнорирует NodeLabels когда вы используете его с ZData.
Пример: 'NodeLabels','on'
Типы данных: char | string
ElementLabels — Метки элемента'off' (значение по умолчанию) | 'on'Элемент помечает в виде разделенной запятой пары, состоящей из 'ElementLabels' и 'off' или 'on'.
pdeplot игнорирует ElementLabels когда вы используете его с ZData.
Пример: 'ElementLabels','on'
Типы данных: char | string
Deformation — Данные для графического вывода деформированной формыDisplacement свойство StaticStructuralResults объектДанные для графического вывода деформированной формы для модели структурного анализа в виде разделенной запятой пары, состоящей из 'Deformation' и Displacement свойство StaticStructuralResults объект.
В недеформированной форме центральные узлы в квадратичных сетках всегда добавляются на полурасстоянии между углами. Когда вы строите деформированную форму, центральные узлы могут переехать от центров ребра.
Пример: 'Deformation',structuralresults.Displacement
DeformationScaleFactor — Масштабный коэффициент для графического вывода деформированной формыМасштабный коэффициент для графического вывода деформированной формы в виде разделенной запятой пары, состоящей из 'DeformationScaleFactor' и вещественное число. Используйте этот аргумент с Deformation пара "имя-значение". Значение по умолчанию задано внутренне, на основе размерностей геометрии и величины деформации.
Пример: 'DeformationScaleFactor',100
Типы данных: double
ColorBar — Индикатор, чтобы включать цветную полосу'on' (значение по умолчанию) | 'off'Индикатор, чтобы включать цветную полосу в виде разделенной запятой пары, состоящей из 'ColorBar' и 'on' или 'off'. Задайте 'on' отобразить панель, дающую числовые значения, раскрашивает график. Для получения дополнительной информации смотрите colorbar. pdeplot функционируйте использует палитру, заданную в ColorMap пара "имя-значение".
Пример: 'ColorBar','off'
Типы данных: char | string
ColorMap палитра'cool' (значение по умолчанию) | ColorMap значение или матрица таких значенийПалитра в виде разделенной запятой пары, состоящей из 'ColorMap' и значение, представляющее встроенную палитру или матрицу палитры. Для получения дополнительной информации смотрите colormap.
ColorMap должен использоваться с XYData пара "имя-значение".
Пример: 'ColorMap','jet'
Типы данных: double | char | string
Mesh — Индикатор, чтобы показать mesh'off' (значение по умолчанию) | 'on'Индикатор, чтобы показать mesh в виде разделенной запятой пары, состоящей из 'Mesh' и 'on' или 'off'. Задайте 'on' показать mesh в графике.
Пример: 'Mesh','on'
Типы данных: char | string
Title — Заголовок графикаЗаголовок графика в виде разделенной запятой пары, состоящей из 'Title' и вектор символов.
Пример: 'Title','Solution Plot'
Типы данных: char | string
FaceAlpha — Поверхностная прозрачность для 3-D геометрии0 через 1Поверхностная прозрачность для 3-D геометрии в виде разделенной запятой пары, состоящей из 'FaceAlpha' и вещественное число от 0 через 1. Значение по умолчанию 1 не указывает ни на какую прозрачность. Значение 0 указывает на полную прозрачность.
Пример: 'FaceAlpha',0.5
Типы данных: double
Contour — Индикатор, чтобы построить кривые уровня'off' (значение по умолчанию) | 'on'Индикатор, чтобы построить кривые уровня в виде разделенной запятой пары, состоящей из 'Contour' и 'off' или 'on'. Задайте 'on' построить кривые уровня для XYData данные. Задайте уровни с Levels пара "имя-значение".
Пример: 'Contour','on'
Типы данных: char | string
Levels — Уровни для контурного графикаУровни для контурного графика в виде разделенной запятой пары, состоящей из 'Levels' и положительное целое число или вектор из значений уровня.
Положительное целое число — График Levels как равномерно распределенные контуры.
Вектор — График очерчивает в значениях в Levels.
Чтобы получить контурный график, установите Contour пара "имя-значение" к 'on'.
Пример: 'Levels',16
Типы данных: double
h — Указатели на графические объектыУказатели на графические объекты, возвращенные как вектор.
quiver plot является графиком векторного поля. Это также называется flow plot.
Стрелки показывают направление поля с длинами стрел, показывающих относительные размеры полевой силы. Для получения дополнительной информации на графиках полей градиента, смотрите quiver.
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.