robust H∞ performance определяет количество, как смоделированная неопределенность влияет на эффективность обратной связи. Уровень здесь измерен с H ∞ норма (пиковое усиление) передаточной функции интереса, такого как это от воздействия до сигналов ошибки. (См. Эффективность H-бесконечности.)
Для системы T (s) устойчивый H ∞ эффективность μ является наименьшим значением γ, таким образом, что пиковое усиление T остается ниже γ по причине неопределенности до 1/γ в нормированных единицах. Например:
μ = 0,5 средних значения, что || T (s) || ∞ остается ниже 0.5 по причине неопределенности до дважды неопределенности, заданной в T. Усиление худшего случая для заданной неопределенности обычно меньше.
μ = 2 средних значения, что || T (s) || ∞ остается ниже 2 по причине неопределенности до половины неопределенности, заданной в T. Для этого значения усиление худшего случая для полной заданной неопределенности может быть намного больше. Это может даже быть бесконечно, означая, что система не остается устойчивой по полному спектру заданной неопределенности.
Количество μ является пиковым значением по частоте μ structured singular value (ω) для неопределенности, заданной в T. Это количество является обобщением сингулярного значения для неопределенных систем. Это зависит от структуры неопределенности в системе. На практике μ затрудняет, чтобы вычислить точно, таким образом, программное обеспечение вместо этого вычисляет нижние и верхние границы, и . Верхняя граница имеет несколько приложений в проекте системы управления и анализе. Вы можете:
Использование musyn спроектировать контроллер для неопределенного объекта, который минимизирует из системы с обратной связью. В дополнение к получившемуся контроллеру, musyn возвращает соответствующее значение в CLperf выходной аргумент.
Использование musynperf оцените устойчивую эффективность неопределенной системы. Эта функция возвращает нижние и верхние границы на μ, значения неопределенности, которые дают к пику μ и другая информация об устойчивой эффективности с обратной связью.
Чтобы изучить расчет устойчивого H ∞ эффективность, считайте неопределенную систему T (s), смоделированный как фиксированный фрагмент T 0 и неопределенный фрагмент Δunc/γ.

Δunc собирает неопределенные элементы {Δ1, …, ΔN}.
Каждый Δj является произвольной действительной, комплексной, или динамической неопределенностью, которая нормирована таким образом что ||Δj || ∞ ≤ 1. Факторный γ настраивает уровень неопределенности.
Предположим это для системы, смоделированной как в схеме (a),
|| T || ∞ ≤ γ для всего ||Δunc || ∞ ≤ 1.
Теоремой маленького усиления (см. [1]), это устойчивое условие эффективности эквивалентно утверждению, что система схемы (b), LFT (Δperf/γ, T), устойчиво для всех для всего ||Δperf || ∞ ≤ 1.

Δperf называется performance block. Расширьте T как в схеме (a) и группе Δperf с неопределенными блоками Δunc, чтобы задать новый блок Δ,
Результатом является система в следующей схеме.

Таким образом устойчивое условие эффективности в системе схемы (a) эквивалентно условию устойчивости на схеме (c), или
Устойчивым μ эффективности является самый маленький γ, для которого это условие устойчивости содержит. Эквивалентно, 1/μ является самым большим уровнем неопределенности 1/γ, для которого система схемы (c) надежно устойчива. Другими словами, 1/μ является устойчивым запасом устойчивости обратной связи схемы (c) для увеличенной неопределенности Δ. (Для получения дополнительной информации об устойчивых запасах устойчивости смотрите Анализ Робастности и Худшего Случая.)
Чтобы получить оценку на верхней границе μ, программное обеспечение вводит scalings. Если система в схеме (c) устойчива для всего ||Δ || ∞ ≤ 1, то система следующей схемы также устойчива для любого обратимого D.
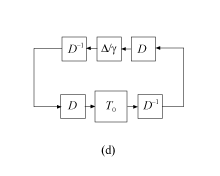
Если поездки на работу D с Δ, то система схемы (d) совпадает с системой в следующей схеме.
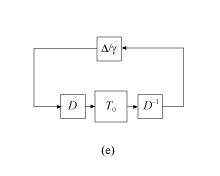
Матрицы D, которые структурно коммутируются с Δ, называются масштабированиями D. Они могут быть зависимым частоты, который обозначается D (ω).
Define как:
Для оптимального D* (ω) и любой γ ≥ ,
Поэтому теоремой маленького усиления, система схемы (e) устойчива для всего ||Δ || ∞ ≤ 1. Из этого следует, что 1/γ ≤ 1/μ, или γ ≤ μ, потому что 1/μ является устойчивым запасом устойчивости. Следовательно, μ ≤ , так, чтобы верхняя граница для устойчивой эффективности μ. Эта верхняя граница количество, вычисленное musynperf и оптимизированный musyn.
Когда все неопределенные элементы Δj являются комплексными или динамика LTI, программное обеспечение аппроксимирует путем выбора сетки частоты {ω 1, …, ωN}. В каждой точке частоты программное обеспечение решает оптимальную задачу масштабирования
Это затем устанавливает к самому большому результату по всем частотам в сетке,
Когда некоторые Δj действительны, возможно получить менее консервативную верхнюю границу при помощи дополнительных масштабирований под названием масштабирования G. В этом случае, является самым маленьким по частоте, таким образом, что
для некоторого Dr (ωi), Dc (ωi) и Gcr (ωi). Эти зависимые частотой матрицы являются масштабированиями G и D.
musyn команда синтезирует устойчивые контроллеры, использующие итеративный процесс, который оптимизирует устойчивую эффективность . Изучить, как использовать musyn, смотрите, что Устойчивое Проектирование контроллера Использует Mu-Synthesis. Для получения дополнительной информации о musyn алгоритм, см. Процесс Итерации D-K.
[1] Skogestad, S. и я. Postlethwaite, Многомерное Управление с обратной связью: Анализ и проектирование, 2-й редактор Западный Сассекс, Англия: John Wiley & Sons, 2005, стр 156, 306.