Постройте 3-D неявное уравнение или функцию
fimplicit3( строит 3-D неявное уравнение или функциональный f)f(x,y,z) на интервале по умолчанию [-5 5] для xY, и z.
fimplicit3( графики f,[xmin
xmax ymin ymax zmin zmax])f(x,y,z) на интервале [xmin xmax] для x, [ymin ymax] для y, и [zmin zmax] для z. fimplicit3 функциональное использование symvar заказать интервалы присвоения и переменные.
fimplicit3(___, использование LineSpec)LineSpec установить стиль линии, символ маркера и цвет поверхности.
fimplicit3(___, задает свойства линии с помощью одного или нескольких Name,Value)Name,Value парные аргументы. Используйте эту опцию с любыми комбинациями входных аргументов в предыдущих синтаксисах.
fimplicit3( графики в осях с объектом ax,___)ax вместо объекта текущей системы координат gca.
fi = fimplicit3(___)
Постройте гиперболоид при помощи fimplicit3. fimplicit3 графики функций на интервале по умолчанию для , , и .
syms x y z fimplicit3(x^2 + y^2 - z^2)

Постройте гиперболоид, заданный функцией . fimplicit3 графики функций на интервале по умолчанию для , , и .
syms f(x,y,z)
f(x,y,z) = x^2 + y^2 - z^2;
fimplicit3(f)
Задайте интервал графического вывода путем определения второго аргумента к fimplicit3. Постройте верхнюю половину гиперболоида путем определения интервала для и , используйте интервал по умолчанию .
syms x y z f = x^2 + y^2 - z^2; interval = [-5 5 -5 5 0 5]; fimplicit3(f, interval)

Постройте неявное уравнение на интервале для всех осей.
Создайте метки деления оси X путем охвата пределов оси X с промежутками в pi/2. Преобразуйте пределы по осям точным множителям pi/2 при помощи round и получите символьные значения деления в S. Отобразите эти метки деления при помощи XTick свойство. Создайте метки оси X при помощи arrayfun применять texlabel к S. Отобразите эти метки при помощи XTickLabel свойство. Повторите эти шаги для оси Y.
Чтобы использовать LaTeX в графиках, смотрите latex.
syms x y z eqn = x*sin(y) + z*cos(x); fimplicit3(eqn,[-2*pi 2*pi]) title('xsin(y) + zcos(x) for -2\pi < x < 2\pi and -2\pi < y < 2\pi') xlabel('x') ylabel('y') ax = gca; S = sym(ax.XLim(1):pi/2:ax.XLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.XTick = double(S); ax.XTickLabel = arrayfun(@texlabel,S,'UniformOutput',false); S = sym(ax.YLim(1):pi/2:ax.YLim(2)); S = sym(round(vpa(S/pi*2))*pi/2); ax.YTick = double(S); ax.YTickLabel = arrayfun(@texlabel, S, 'UniformOutput', false);

Постройте неявную поверхность с различными стилями линии для различных значений для , используйте пунктирную линию с зелеными точечными маркерами. Для , используйте LineWidth из 1 и зеленый цвет поверхности. Для , выключите линии установкой EdgeColor к none.
syms x y z f = x^2 + y^2 - z^2; fimplicit3(f,[-5 5 -5 5 -5 -2],'--.','MarkerEdgeColor','g') hold on fimplicit3(f,[-5 5 -5 5 -2 2],'LineWidth',1,'FaceColor','g') fimplicit3(f,[-5 5 -5 5 2 5],'EdgeColor','none')

Постройте неявную поверхность . Задайте выход, чтобы сделать fimplicit3 возвратите объект графика.
syms x y z f = 1/x^2 - 1/y^2 + 1/z^2; fi = fimplicit3(f)

fi =
ImplicitFunctionSurface with properties:
Function: 1/x^2 - 1/y^2 + 1/z^2
EdgeColor: [0 0 0]
LineStyle: '-'
FaceColor: 'interp'
Show all properties
Покажите только положительную ось X путем установки XRange свойство fi к [0 5]. Удалите линии путем установки EdgeColor свойство к 'none'. Визуализируйте невидимые поверхности путем создания графика прозрачным путем установки FaceAlpha свойство к 0.8.
fi.XRange = [0 5];
fi.EdgeColor = 'none';
fi.FaceAlpha = 0.8;
Управляйте разрешением неявной объемной поверхностной диаграммы при помощи 'MeshDensity' опция. Увеличение 'MeshDensity' может сделать более сглаженные, более точные графики при уменьшении 'MeshDensity' может увеличить скорость графического вывода.
Разделите фигуру на два при помощи subplot. В первом подграфике постройте неявную поверхность . Поверхность имеет большие разрывы. Устраните эту проблему путем увеличения 'MeshDensity' к 40 во втором подграфике. fimplicit3 заполняет разрывы, показывающие это путем увеличения 'MeshDensity' вы увеличили разрешение графика.
syms x y z f = sin(1/(x*y*z)); subplot(2,1,1) fimplicit3(f) title('Default MeshDensity = 35') subplot(2,1,2) fimplicit3(f,'MeshDensity',40) title('Increased MeshDensity = 40')

Примените вращение и перевод в неявную объемную поверхностную диаграмму торуса.
Торус может быть задан неявным уравнением в Декартовых координатах как
где
радиус трубы
расстояние от центра трубы к центру торуса
Задайте значения для и как 1 и 5, соответственно. Постройте торус с помощью fimplicit3.
syms x y z a = 1; R = 4; f(x,y,z) = (x^2+y^2+z^2+R^2-a^2)^2 - 4*R^2*(x^2+y^2); fimplicit3(f) hold on
Примените вращение к торусу вокруг ось. Задайте матрицу вращения. Вращайте торус 90 градусами или радианы. Переключите центр торуса 5 вперед ось.
alpha = pi/2;
Rx = [1 0 0;
0 cos(alpha) sin(alpha);
0 -sin(alpha) cos(alpha)];
r = [x; y; z];
r_90 = Rx*r;
g = subs(f,[x,y,z],[r_90(1)-5,r_90(2),r_90(3)]);Добавьте второй график вращаемого и переведенного торуса к существующему графику.
fimplicit3(g)
axis([-5 10 -5 10 -5 5])
hold off
f — 3-D неявное уравнение или функция, чтобы построить3-D неявное уравнение или функция, чтобы построить в виде символьного уравнения, выражения или функции. Если выражение или функция заданы, то fimplicit3 принимает правый размер, чтобы быть 0.
[min max] — Строя интервал для x-, y-и z-осейСтроя интервал для x-, y-и z-осей в виде вектора из двух чисел. Значением по умолчанию является [-5 5].
[xmin xmax ymin ymax zmin zmax] — Строя интервал для x-, y-и z-осейСтроя интервал для x-, y-и z-осей в виде вектора из шести чисел. Значением по умолчанию является [-5 5 -5 5 -5 5].
ax Объект осейОбъект осей. Если вы не задаете объект осей, то fimplicit3 использует текущую систему координат.
LineSpec — Стиль линии, маркер и цветСтиль линии, цвет и маркер задается как символ или строка символов. Символы могут появиться в любом порядке. Вы не должны задавать все три характеристики (стиль линии, маркер и цвет). Например, если вы не используете стиль линии и задаете маркер, затем график показывает только маркер и никакую линию.
Пример: '--or' красная пунктирная линия с круговыми маркерами
| Стиль линии | Описание | Получившаяся линия |
|---|---|---|
'-' | Сплошная линия |
|
'--' | Пунктирная линия |
|
':' | Пунктирная линия |
|
'-.' | Штрих-пунктирная линия |
|
| Маркер | Описание | Получившийся маркер |
|---|---|---|
'o' | Круг |
|
'+' | Знак «плюс» |
|
'*' | Звездочка |
|
'.' | Точка |
|
'x' | Крест |
|
'_' | Горизонтальная линия |
|
'|' | Вертикальная линия |
|
's' | Квадрат |
|
'd' | Ромб |
|
'^' | Треугольник, направленный вверх |
|
'v' | Нисходящий треугольник |
|
'>' | Треугольник, указывающий вправо |
|
'<' | Треугольник, указывающий влево |
|
'p' | Пентаграмма |
|
'h' | Гексаграмма |
|
| Название цвета | Краткое название | Триплет RGB | Внешний вид |
|---|---|---|---|
'red' | 'r' | [1 0 0] |
|
'green' | 'g' | [0 1 0] |
|
'blue' | 'b' | [0 0 1] |
|
'cyan'
| 'c' | [0 1 1] |
|
'magenta' | 'm' | [1 0 1] |
|
'yellow' | 'y' | [1 1 0] |
|
'black' | 'k' | [0 0 0] |
|
'white' | 'w' | [1 1 1] |
|
Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.
'Marker','o','MarkerFaceColor','red'Перечисленные здесь свойства являются только подмножеством. Для полного списка смотрите ImplicitFunctionSurface Properties.
MeshDensity — Количество оценки указывает на направлениеКоличество оценки указывает на направление в виде номера. Значением по умолчанию является 35.
Пример: 100
EdgeColor 'LineColor' 'interp' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет линии в виде 'interp', триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название. Значение триплета RGB по умолчанию [0 0 0] соответствует черный. 'interp' значение окрашивает ребра на основе ZData значения.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или строковым скаляром, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Не применяется | Не применяется | Не применяется | Нет цвета |
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию MATLAB® использование во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
LineStyle — Стиль линии'-' (значение по умолчанию) | '--' | ':' | '-.' | 'none'Стиль линии в виде одной из опций перечислен в этой таблице.
| Стиль линии | Описание | Получившаяся линия |
|---|---|---|
'-' | Сплошная линия |
|
'--' | Пунктирная линия |
|
':' | Пунктирная линия |
|
'-.' | Штрих-пунктирная линия |
|
'none' | Никакая линия | Никакая линия |
LineWidth 'LineWidth' Ширина линии в виде положительного значения в точках, где 1 точка = 1/72 дюйма. Если у линии есть маркеры, ширина линии также влияет на края маркера.
Ширина линии не может быть более тонкой, чем ширина пикселя. Если вы устанавливаете ширину линии на значение, которое меньше ширины пикселя в вашей системе, отображения линии как один пиксель шириной.
Marker — Символ маркера'none' (значение по умолчанию) | 'o' | '+' | '*' | '.' | ...Символ маркера в виде одного из значений перечислен в этой таблице. По умолчанию объект не отображает маркеры. Определение символа маркера добавляет маркеры в каждой точке данных или вершине.
| Маркер | Описание | Получившийся маркер |
|---|---|---|
'o' | Круг |
|
'+' | Знак «плюс» |
|
'*' | Звездочка |
|
'.' | Точка |
|
'x' | Крест |
|
'_' | Горизонтальная линия |
|
'|' | Вертикальная линия |
|
's' | Квадрат |
|
'd' | Ромб |
|
'^' | Треугольник, направленный вверх |
|
'v' | Нисходящий треугольник |
|
'>' | Треугольник, указывающий вправо |
|
'<' | Треугольник, указывающий влево |
|
'p' | Пентаграмма |
|
'h' | Гексаграмма |
|
'none' | Никакие маркеры | Не применяется |
MarkerEdgeColor — Цвет контура маркера'auto' (значение по умолчанию) | триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет контура маркера в виде 'auto', триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название. Значение по умолчанию 'auto' использует тот же цвет в качестве EdgeColor свойство.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или строковым скаляром, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Не применяется | Не применяется | Не применяется | Нет цвета |
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию использованием MATLAB во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Пример: [0.5 0.5 0.5]
Пример: 'blue'
Пример: '#D2F9A7'
MarkerFaceColor — Цвет заливки маркера'none' (значение по умолчанию) | 'auto' | Триплет RGB | шестнадцатеричный цветовой код | 'r' | 'g' | 'b' | ...Цвет заливки маркера в виде 'auto', триплет RGB, шестнадцатеричный цветовой код, название цвета или краткое название. 'auto' значение использует тот же цвет в качестве MarkerEdgeColor свойство.
Для пользовательского цвета задайте триплет RGB или шестнадцатеричный цветовой код.
Триплет RGB представляет собой трехэлементный вектор-строку, элементы которого определяют интенсивность красных, зеленых и синих компонентов цвета. Интенсивность должна быть в области значений [0,1]; например, [0.4 0.6 0.7].
Шестнадцатеричный цветовой код является вектором символов или строковым скаляром, который запускается с символа хеша (#) сопровождаемый тремя или шестью шестнадцатеричными цифрами, которые могут лежать в диапазоне от 0 к F. Значения не являются чувствительными к регистру. Таким образом, цветовые коды '#FF8800', '#ff8800', '#F80', и '#f80' эквивалентны.
Кроме того, вы можете задать имена некоторых простых цветов. Эта таблица приводит опции именованного цвета, эквивалентные триплеты RGB и шестнадцатеричные цветовые коды.
| Название цвета | Краткое название | Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|---|---|
'red' | 'r' | [1 0 0] | '#FF0000' |
|
'green' | 'g' | [0 1 0] | '#00FF00' |
|
'blue' | 'b' | [0 0 1] | '#0000FF' |
|
'cyan'
| 'c' | [0 1 1] | '#00FFFF' |
|
'magenta' | 'm' | [1 0 1] | '#FF00FF' |
|
'yellow' | 'y' | [1 1 0] | '#FFFF00' |
|
'black' | 'k' | [0 0 0] | '#000000' |
|
'white' | 'w' | [1 1 1] | '#FFFFFF' |
|
'none' | Не применяется | Не применяется | Не применяется | Нет цвета |
Вот являются триплеты RGB и шестнадцатеричные цветовые коды для цветов по умолчанию использованием MATLAB во многих типах графиков.
| Триплет RGB | Шестнадцатеричный цветовой код | Внешний вид |
|---|---|---|
[0 0.4470 0.7410] | '#0072BD' |
|
[0.8500 0.3250 0.0980] | '#D95319' |
|
[0.9290 0.6940 0.1250] | '#EDB120' |
|
[0.4940 0.1840 0.5560] | '#7E2F8E' |
|
[0.4660 0.6740 0.1880] | '#77AC30' |
|
[0.3010 0.7450 0.9330] | '#4DBEEE' |
|
[0.6350 0.0780 0.1840] | '#A2142F' |
|
Example: [0.3 0.2 0.1]
Пример: 'green'
Пример: '#D2F9A7'
MarkerSize 'MarkerSize' Размер маркера в виде положительного значения в точках, где 1 точка = 1/72 дюйма.
fi — Один или несколько объектовОдин или несколько объектов, возвращенных как скаляр или вектор. Объект является объектом подложки неявной функции. Можно использовать эти объекты запросить и изменить свойства определенной линии. Для получения дополнительной информации смотрите ImplicitFunctionSurface Properties.
fimplicit3 присваивает символьные переменные в f к x ось, y ось, затем z ось, и symvar определяет порядок переменных, которые будут присвоены. Поэтому переменная и имена оси не могут соответствовать. Обеспечивать fimplicit3 чтобы присвоить x, y или z к его соответствующей оси, создает символьную функцию, чтобы построить, затем передать символьную функцию fimplicit3.
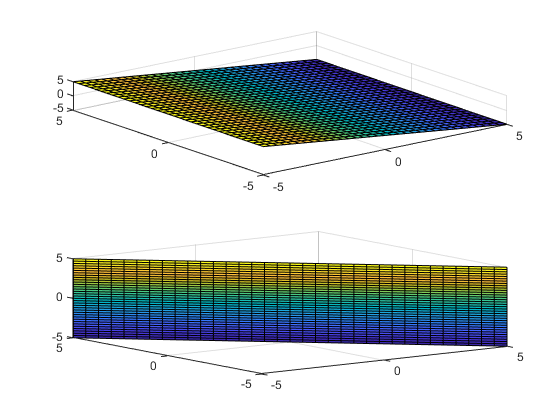
Например, следующий код строит корни неявной функции f (x, y, z) = x + z двумя способами. Первым путем силы fimplicit3 присваивать x и z к их соответствующим осям. Вторым способом, fimplicit3 подчиняется symvar определить присвоение оси и переменный порядок: fimplicit3 присвоения x и z к x и осям y, соответственно.
syms x y z; f(x,y,z) = x + z; figure; subplot(2,1,1) fimplicit3(f); view(-38,71); subplot(2,1,2) fimplicit3(f(x,y,z)); % Or fimplicit3(x + z);
У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.