Графика MATLAB® задает поверхность z-координатами точек выше прямоугольной сетки в x-y плоскости. График формируется путем присоединения смежных точек с прямыми линиями. Объемные поверхностные диаграммы полезны для визуализации матриц, которые являются слишком большими, чтобы отобразиться в числовой форме и для функций построения графика двух переменных.
MATLAB может создать различные формы объемных поверхностных диаграмм. Сетчатые графики являются каркасными поверхностями, которые окрашивают только линии, соединяющие определяющие точки. Объемные поверхностные диаграммы отображают и соединительные линии и полигоны поверхности в цвете. Эта таблица приводит различные формы.
Функция | Используемый, чтобы создать |
|---|---|
mesh, surf | Объемная поверхностная диаграмма |
meshc, surfc | Объемная поверхностная диаграмма с контурным графиком ниже его |
meshz | Объемная поверхностная диаграмма с графиком занавеса (ссылочная плоскость) |
pcolor | График плоской поверхности (значение пропорционально только, чтобы окрасить), |
surfl | Объемная поверхностная диаграмма освещается от заданного направления |
поверхность | Низкоуровневая функция (на котором высокоуровневые функции базируются) для создания поверхностных графических объектов |
Эти функции полезны, когда необходимо реструктурировать и интерполировать данные так, чтобы можно было представлять это данные как поверхность.
Функция | Используемый, чтобы создать |
|---|---|
meshgrid | Прямоугольная сетка на 2D и 3-D пробеле |
griddata | Интерполируйте данные, имеющий разброс |
griddedInterpolant | Interpolant для данных с координатной сеткой |
scatteredInterpolant | Интерполируйте данные, имеющий разброс |
Для обсуждения того, как интерполировать данные, смотрите Интерполирующие Данные С координатной сеткой и Интерполяцию данных, имеющих разброс.
mesh и команды surf создают 3-D объемные поверхностные диаграммы матричных данных. Если Z является матрицей, для которой элементы Z(i,j) задают высоту поверхности по базовой сетке (i,j), то
mesh(Z)
генерирует цветное, каркасное представление поверхности и отображает его в 3-D представлении. Точно так же
surf(Z)
генерирует цветное, фасетное представление поверхности и отображает его в 3-D представлении. Обычно, фасеты являются четырехугольниками, каждый из которых является постоянным цветом, обрисованным в общих чертах с черными строками mesh, но команда shading позволяет вам устранять строки mesh (shading flat) или выбирать интерполированную штриховку через фасет (shading interp).
Свойства объекта подложки обеспечивают дополнительное управление общим видом поверхности. Можно задать граничные стили линии, маркеры вершины, окраску поверхности, подсветку характеристик, и так далее.
Чтобы отобразить функцию двух переменных, z = f (x,y), генерируют X и матрицы Y, состоящие из повторных строк и столбцов, соответственно, по области функции. Вы будете использовать эти матрицы, чтобы оценить и изобразить функцию в виде графика.
Функция meshgrid преобразовывает область, заданную двумя векторами, x и y, в матрицы X и Y. Вы затем используете эти матрицы, чтобы выполнить функции двух переменных: строки X являются копиями векторного x, и столбцы Y являются копиями векторного y.
Чтобы проиллюстрировать использование meshgrid, рассмотрите функция sinc или sin(r)/r. Чтобы выполнить эту функцию между-8 и 8 в обоих x и y, вы должны передать только один аргумент вектора meshgrid, который затем используется в обоих направлениях.
[X,Y] = meshgrid(-8:.5:8); R = sqrt(X.^2 + Y.^2) + eps;
Матричный R содержит расстояние от центра матрицы, которая является источником. Добавление eps предотвращает деление нулем (на следующем шаге), который производит значения Inf в данных.
Формирование sinc функционируют и графическое изображение Z с результатами mesh на 3-D поверхности.
Z = sin(R)./R; figure mesh(X,Y,Z)
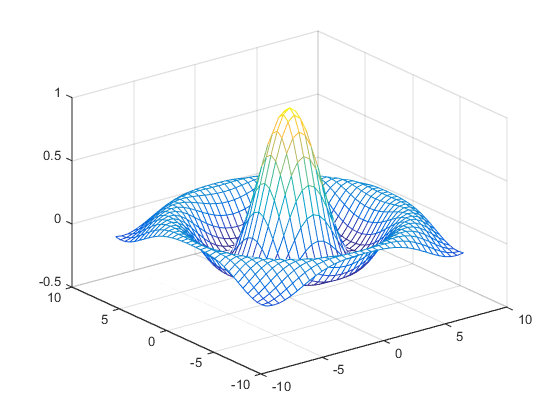
По умолчанию MATLAB удаляет строки, которые скрыты от представления в сетчатых графиках, даже при том, что поверхности графика не заполнены. Можно отключить удаление невидимой линии и позволить поверхностям сетчатого графика быть прозрачными с командой hidden:
hidden off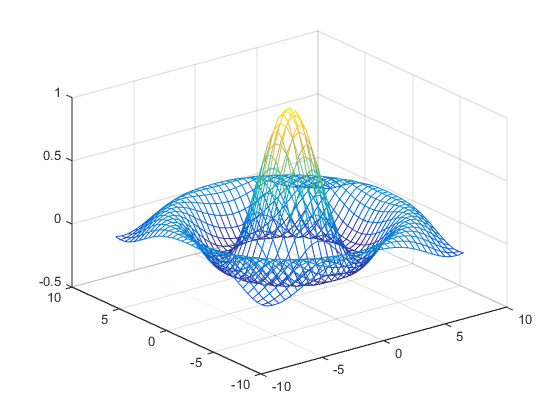
MATLAB обеспечивает много методов, которые могут улучшить информационное содержимое ваших графиков. Например, этот график функции sinc использует те же данные в качестве предыдущего графика, но использует подсветку, корректировки представления и различную палитру, чтобы подчеркнуть форму графической функции (daspect, axis, view, camlight).
figure colormap hsv surf(X,Y,Z,'FaceColor','interp',... 'EdgeColor','none',... 'FaceLighting','gouraud') daspect([5 5 1]) axis tight view(-50,30) camlight left
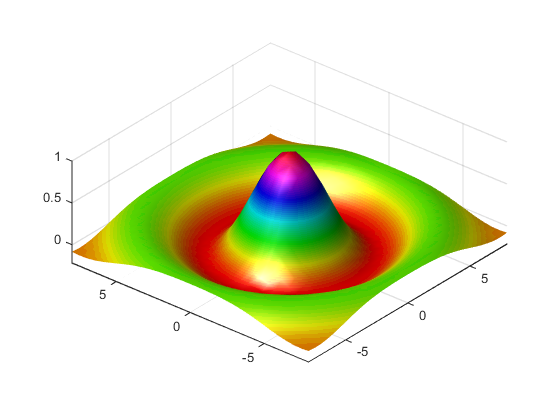
Смотрите, что surf функционирует для получения дополнительной информации об объемных поверхностных диаграммах.
Можно использовать meshgrid, чтобы создать сетку однородно точек выборочных данных, в которых можно оценить и изобразить в виде графика функцию sinc. MATLAB затем создает объемную поверхностную диаграмму путем соединения соседних элементов матрицы, чтобы сформировать сетку четырехугольников.
Чтобы произвести объемную поверхностную диаграмму из неоднородно выборочных данных, используйте scatteredInterpolant, чтобы интерполировать значения в однородно расположенных с интервалами точках, и затем использовать mesh и surf обычным способом.
Этот пример выполняет функцию sinc , наугад указывает в определенной области значений и затем генерирует однородно выборочные данные для отображения как объемная поверхностная диаграмма. Процесс включает эти задачи:
Используйте linspace, чтобы сгенерировать равномерно распределенные значения в области значений ваших неравномерно выборочных данных.
Используйте meshgrid, чтобы сгенерировать сетку графического изображения с выводом linspace.
Используйте scatteredInterpolant, чтобы интерполировать нерегулярно выборочные данные к расположенной с равными интервалами сетке, возвращенной meshgrid.
Используйте функцию построения графика, чтобы отобразить данные.
Сгенерируйте неравномерно выборочные данные в области значений [-8, 8] и используйте ее, чтобы выполнить функцию:
x = rand(100,1)*16 - 8; y = rand(100,1)*16 - 8; r = sqrt(x.^2 + y.^2) + eps; z = sin(r)./r;
Функция linspace обеспечивает удобный способ создать однородно распределенные данные с желаемым числом элементов. Следующие операторы производят векторы в области значений случайных данных с тем же разрешением как сгенерированный-8:.5:8 оператором в предыдущем примере sinc:
xlin = linspace(min(x),max(x),33); ylin = linspace(min(y),max(y),33);
Теперь используйте эти точки, чтобы сгенерировать однородно расположенную с интервалами сетку:
[X,Y] = meshgrid(xlin,ylin);
Ключ к этому процессу должен использовать scatteredInterpolant, чтобы интерполировать значения функции в однородно расположенных с интервалами точках, на основе значений функции в исходных точках данных (которые случайны в этом примере). Этот оператор использует линейную интерполяцию по умолчанию, чтобы сгенерировать новые данные:
f = scatteredInterpolant(x,y,z); Z = f(X,Y);
Постройте график интерполированного и неоднородных данных, чтобы произвести:
figure mesh(X,Y,Z) %interpolated axis tight; hold on plot3(x,y,z,'.','MarkerSize',15) %nonuniform
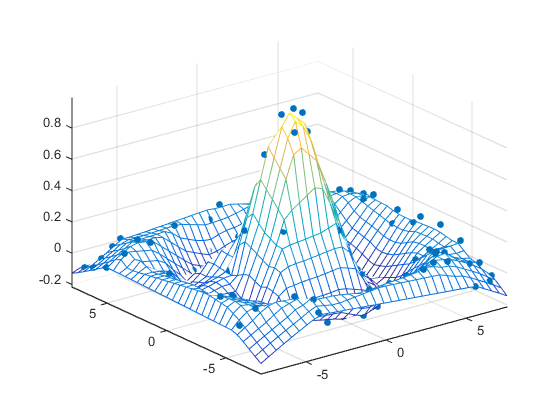
Предположим, что у вас есть набор данных со следующим (X, Y, Z) триплеты:
| X | Y | Z |
|---|---|---|
| 1 | 1 | 152 |
| 2 | 1 | 89 |
| 3 | 1 | 100 |
| 4 | 1 | 100 |
| 5 | 1 | 100 |
| 1 | 2 | 103 |
| 2 | 2 | 0 |
| 3 | 2 | 100 |
| 4 | 2 | 100 |
| 5 | 2 | 100 |
| 1 | 3 | 89 |
| 2 | 3 | 13 |
| 3 | 3 | 100 |
| 4 | 3 | 100 |
| 5 | 3 | 100 |
| 1 | 4 | 115 |
| 2 | 4 | 100 |
| 3 | 4 | 187 |
| 4 | 4 | 200 |
| 5 | 4 | 111 |
| 1 | 5 | 100 |
| 2 | 5 | 85 |
| 3 | 5 | 111 |
| 4 | 5 | 97 |
| 5 | 5 | 48 |
Можно представлять данные, который находится в векторной форме с помощью различных типов графика MATLAB, таких как surf, contour и stem3, первой реструктуризацией данных. Используйте (X, Y) значения, чтобы задать координаты в x-y плоскости, в которой существует значение Z. reshape и функции transpose могут реструктурировать ваши данные так, чтобы (X, Y, Z) триплеты сформировали прямоугольную сетку:
x = reshape(X,5,5)'; y = reshape(Y,5,5)'; z = reshape(Z,5,5)';
Изменение результатов в трех массивах 5 на 5:
x =
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
1 2 3 4 5
y =
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
z =
152 89 100 100 100
103 0 100 100 100
89 13 100 100 100
115 100 187 200 111
100 85 111 97 48Можно теперь представлять значения Z относительно X и y. Например, создайте 3-D график основы:
stem3(x,y,z,'MarkerFaceColor','g')
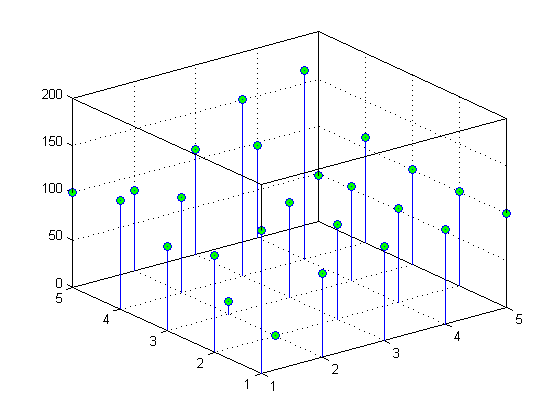
Функции, которые чертят поверхности, могут взять два дополнительных аргумента вектора или матричные аргументы, чтобы описать поверхности с определенными данными x и y. Если Z является матрицей m на n, x является n-вектором, и y является m-вектором, то
mesh(x,y,Z,C)
описывает поверхность mesh с вершинами, имеющими цветной C(i,j) и расположенный в точках
(x(j), y(i), Z(i,j))
где x соответствует столбцам Z и y к его строкам.
Более широко, если X, Y, Z и C являются матрицами тех же размерностей, то
mesh(X,Y,Z,C)
описывает поверхность mesh с вершинами, имеющими цветной C(i,j) и расположенный в точках
(X(i,j), Y(i,j), Z(i,j))
Этот пример использует сферические координаты, чтобы чертить сферу и окрасить ее с шаблоном плюсов и минусов в матрице Адамара, ортогональная матрица используемый в теории кодирования обработки сигналов. Векторы theta и phi находятся в области значений - π ≤ theta ≤ π и - π/2 ≤ phi ≤ π/2. Поскольку theta является вектором - строкой, и phi является вектором - столбцом, умножение, которое производит матрицы X, Y, и Z векторные векторные произведения.
figure k = 5; n = 2^k-1; theta = pi*(-n:2:n)/n; phi = (pi/2)*(-n:2:n)'/n; X = cos(phi)*cos(theta); Y = cos(phi)*sin(theta); Z = sin(phi)*ones(size(theta)); colormap([0 0 0;1 1 1]) C = hadamard(2^k); surf(X,Y,Z,C) axis square
