Сбалансированное усечение вычисляет приближение более низкоуровневое вашей модели путем пренебрежения состояний, которые имеют относительно низкий эффект на полный образцовый ответ. Используя приближение более низкоуровневое, которое сохраняет динамику интереса, может упростить анализ и систему управления. В сбалансированном методе усечения снижения сложности модели, вкладов состояния мер по программному обеспечению сингулярными значениями Ганкеля (см. hsvd), и состояния отбрасываний с меньшими значениями. Существует два способа вычислить модель уменьшаемого порядка сбалансированным усечением:
В командной строке, с помощью команды balred.
В Model Reducer, с помощью метода Balanced Truncation.
Для более общей информации о снижении сложности модели смотрите Основы Снижения сложности модели.
Model Reducer обеспечивает интерактивный инструмент для выполнения снижения сложности модели и исследования и сравнения ответов исходных моделей и моделей уменьшаемого порядка. Аппроксимировать модель сбалансированным усечением в Model Reducer:
Откройте приложение и импортируйте модель LTI, чтобы уменьшать. Например, предположите, что существует модель под названием build в рабочей области MATLAB®. Следующая команда открывает Model Reducer и импортирует модель.
modelReducer(build)
В Data Browser выберите модель, чтобы уменьшать. Нажмите![]() Balanced Truncation.
Balanced Truncation.
Во вкладке Balanced Truncation Model Reducer отображает график частотной характеристики исходной модели и уменьшаемой версии модели. Частотной характеристикой является Диаграмма Боде для моделей SISO и график сингулярного значения для моделей MIMO. Приложение также отображает график сингулярного значения Ганкеля исходной модели.
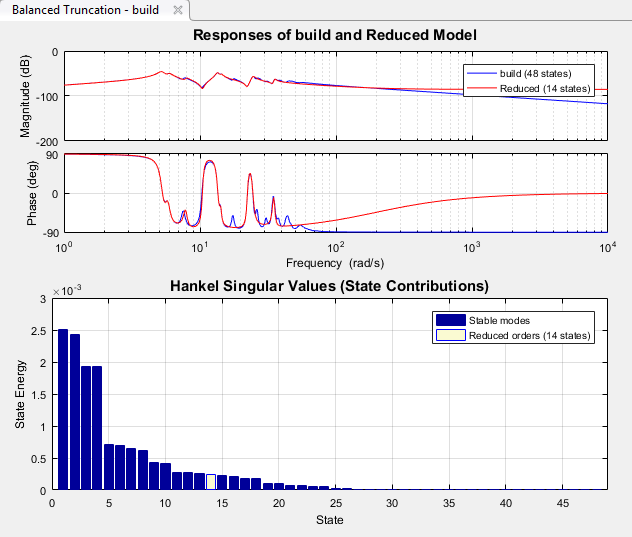
График сингулярного значения Ганкеля показывает относительные энергетические вклады каждого состояния в системе. Model Reducer вычисляет начальный уменьшаемый порядок, основанный на модели на этих значениях. Подсвеченная панель является самым низким энергетическим состоянием в первоначальной модели уменьшаемого порядка. Model Reducer отбрасывает состояния, которые имеют более низкие сингулярные значения Ганкеля, чем подсвеченная панель.
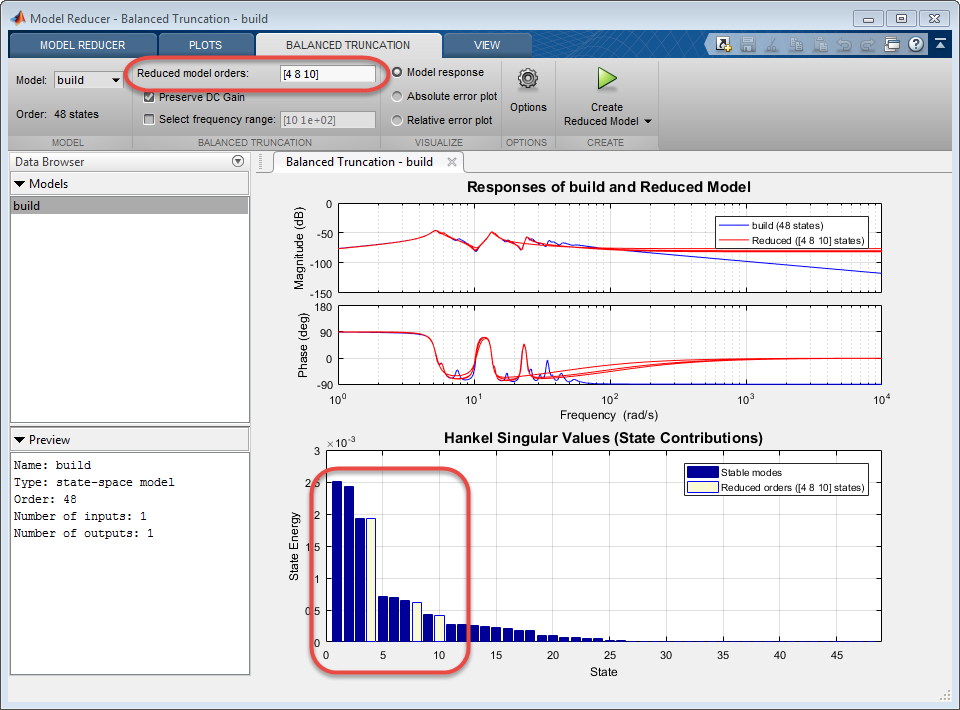
Попробуйте различные порядки упрощенной модели найти модель самую низкоуровневую, которая сохраняет движущие силы, которые важны для вашего приложения. Задавать различные порядки, также:
Введите заказы модели в поле Reduced model orders. Можно ввести одно целое число или массив целых чисел, таких как 10:14 или [8,11,12].
Кликните по панели на графике сингулярного значения Ганкеля задать самое низкое энергетическое состояние модели уменьшаемого порядка. Щелкните при нажатой клавише Ctrl, чтобы задать несколько значений.
Когда вы изменяете заданный порядок упрощенной модели, Model Reducer автоматически вычисляет новую модель уменьшаемого порядка. Если вы задаете порядки многоуровневой модели, Model Reducer вычисляет несколько моделей уменьшаемого порядка и отображает их ответы на графике.
Опционально, исследуйте абсолютную или относительную погрешность между исходной моделью и моделью уменьшаемого порядка, в дополнение к частотной характеристике. Выберите тип диаграммы погрешностей с помощью кнопок на вкладке Balanced Truncation.
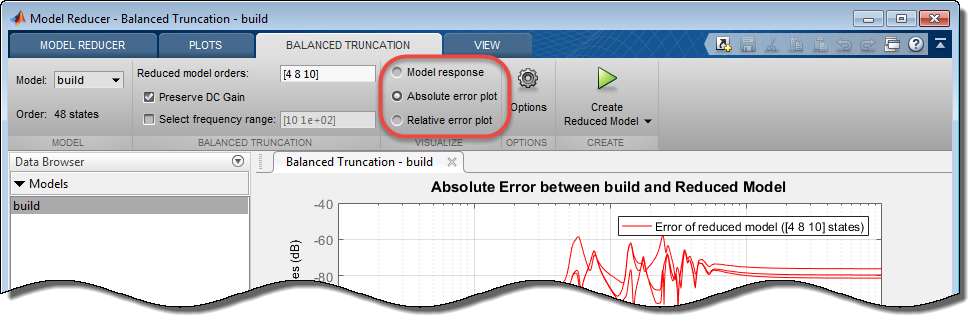
Для получения дополнительной информации об использовании графиков для анализа смотрите, Визуализируют Модели Уменьшаемого Порядка в Приложении Model Reducer.
Если низкочастотные движущие силы не важны для вашего приложения, можно снять флажок Preserve DC Gain. Выполнение поэтому иногда приводит к лучшему соответствию на более высоких частотах между исходными моделями и моделями уменьшаемого порядка.
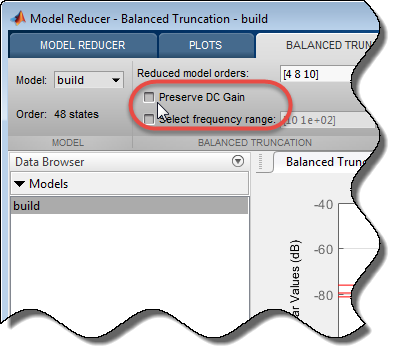
Когда вы проверяете или снимаете флажок Preserve DC Gain, Model Reducer автоматически вычисляет новые модели уменьшаемого порядка. Для получения дополнительной информации об этой опции, смотрите, Выдерживают сравнение Усеченный и DC Совпадающие Образцовые Приближения Младшего разряда.
Опционально, ограничьте вычисление сингулярного значения Ганкеля определенным частотным диапазоном. Такой предел полезен, когда модель имеет режимы вне видимой области к вашему конкретному приложению. Когда вы применяете предел частоты, Model Reducer определяет который состояния обрезать на основе их энергетического вклада в заданном частотном диапазоне только. Пренебрежение энергетических вкладов вне той области значений может привести к даже приближению более низкоуровневому, которое все еще достаточно для вашего приложения.
Чтобы ограничить вычисление сингулярного значения, проверяйте Select frequency range. Затем задайте частотный диапазон:
В текстовом поле, вводя вектор формы [fmin,fmax]. Модулями является rad/TimeUnit, где TimeUnit является свойством TimeUnit модели, вы уменьшаете.
На графике ответа или диаграмме погрешностей, перетаскивая контуры теневой области или самой теневой области. Model Reducer анализирует вклады состояния в теневой области только.
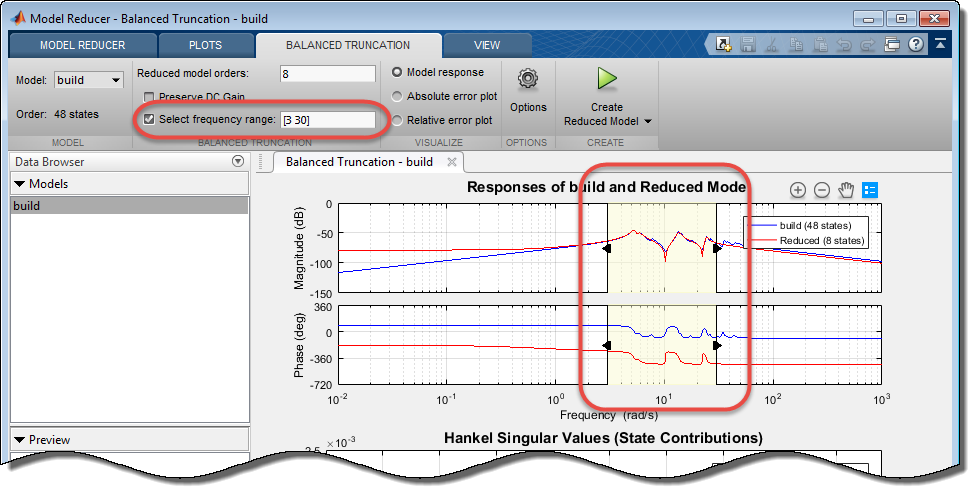
Когда вы проверяете или снимаете флажок Select frequency range или изменяете выбранную область значений, Model Reducer автоматически вычисляет новые модели уменьшаемого порядка.
Проверка Select frequency range автоматически очищает Preserve DC Gain. Чтобы осуществить соответствие DC даже когда с помощью пределов частоты, перепроверьте Preserve DC Gain.
Когда у вас есть одна или несколько упрощенных моделей, которые вы хотите сохранить и анализировать далее, кликнуть![]() . Новые модели появляются в Data Browser. Если вы задали несколько порядков, каждая упрощенная модель появляется отдельно. Имена модели отражают порядок упрощенной модели.
. Новые модели появляются в Data Browser. Если вы задали несколько порядков, каждая упрощенная модель появляется отдельно. Имена модели отражают порядок упрощенной модели.
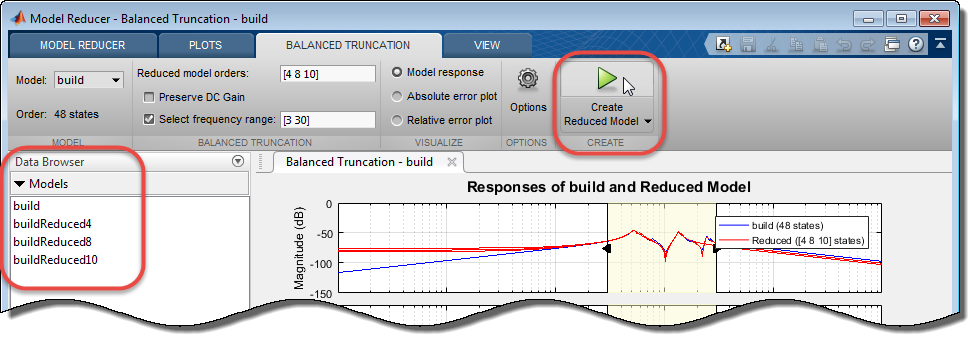
После создания упрощенных моделей в Data Browser можно продолжить изменять параметры сокращения и создать упрощенные модели с различными порядками для анализа и сравнения.
Можно теперь выполнить последующий анализ с упрощенной моделью. Например:
Исследуйте другие ответы уменьшаемой системы, такие как график Николса или переходной процесс. Для этого используйте инструменты на вкладке Plots. Смотрите Визуализируют Модели Уменьшаемого Порядка в Приложении Model Reducer для получения дополнительной информации.
Экспортируйте упрощенные модели в рабочее пространство MATLAB для последующего анализа или системы управления. На вкладке Model Reducer нажмите![]() Export.
Export.
Чтобы создать скрипт MATLAB, можно использовать для дальнейших задач снижения сложности модели в командной строке, нажать Create Reduced Model и выбрать Generate MATLAB Script.
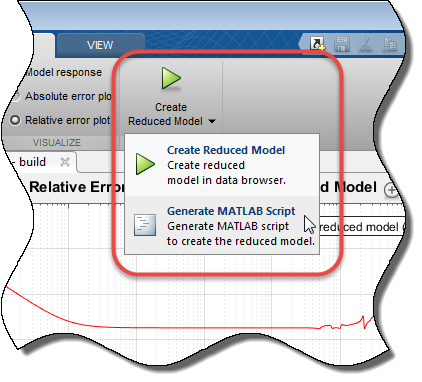
Model Reducer создает скрипт, который использует команду balred, чтобы выполнить снижение сложности модели с параметрами и опциями, которые вы установили на вкладке Balanced Truncation. Скрипт открывается в редакторе MATLAB.
В командной строке используйте balred, чтобы вычислить приближение уменьшаемого порядка модели.
Для этого сначала исследуйте вклад различных состояний к полному поведению модели. Выберите порядок приближения на основе количества состояний, которые делают значительный вклад в полное поведение модели.
В данном примере загрузите старшую модель. hplant является 23-м порядком модель SISO.
load ltiexamples hplant order(hplant)
ans = 23
Исследуйте относительную сумму энергии на состояние в hplant с помощью графика Сингулярного значения Ганкеля (HSV).
hsvplot(hplant)

Маленькие сингулярные значения Ганкеля указывают, что ассоциированные страны способствуют мало поведению системы. График показывает, что два состояния составляют большую часть энергии в системе. Поэтому попытайтесь упростить модель до только первого или второго порядка.
opts = balredOptions('StateElimMethod','Truncate'); hplant1 = balred(hplant,1,opts); hplant2 = balred(hplant,2,opts);
Второй аргумент к balred задает целевой порядок приближения, так, чтобы hplant1 был приближением первого порядка, и hplant2 является приближением второго порядка hplant. По умолчанию balred отбрасывает состояния с самыми маленькими сингулярными значениями Ганкеля и изменяет остающиеся состояния, чтобы сохранить усиление DC системы. Установка опции StateElimMethod к Truncate заставляет balred отбрасывать низкоэнергетические состояния, не изменяя остающиеся состояния.
При работе с моделями уменьшаемого порядка важно проверить, что приближение не вводит погрешности на частотах, которые важны для приложения. Поэтому сравните частотные характеристики исходных и аппроксимированных систем. Для систем MIMO используйте команду sigmaplot. Для этой системы SISO исследуйте Диаграмму Боде.
bodeplot(hplant,hplant2,hplant1) legend('Original','2nd order','1st order')

Приближение второго порядка hplant2 совпадает с исходной системой 23-го порядка очень хорошо, особенно на более низких частотах. Система первого порядка не соответствует также.
В целом, когда вы уменьшаете порядок аппроксимированной модели, частотная характеристика аппроксимированной модели начинает отличаться от исходной модели. Выберите приближение, которое достаточно точно в полосах, которые важны для вас. Например, в системе управления вы можете хотеть хорошую точность в пропускной способности управления. Точность на частотах далеко выше пропускной способности управления, где усиление быстро прокручивается прочь, может быть менее важной.
Можно также подтвердить приближение во временном интервале. Например, исследуйте переходные процессы исходных систем и систем уменьшаемого порядка.
stepplot(hplant,hplant2,'r--',hplant1,'g--') legend('Original','2nd order','1st order','Location','SouthEast')

Этот результат подтверждает, что приближение второго порядка является хорошим соответствием к исходной системе 23-го порядка.
Этот пример показывает, как вычислить аппроксимацию младшим порядком двумя способами и сравнивает результаты. Когда вы вычисляете аппроксимацию младшим порядком сбалансированным методом усечения, вы можете также:
Отбросьте состояния, которые делают самый маленький вклад в поведение системы, изменяя остающиеся состояния, чтобы сохранить усиление DC системы.
Отбросьте низкоэнергетические состояния, не изменяя остающиеся состояния.
Какой метод, который вы выбираете, зависит от того, какие движущие силы являются самыми важными для вашего приложения. В целом сохранение усиления DC происходит за счет точности в динамику более высокой частоты. С другой стороны усечение состояния может привести к большей точности в быстрых переходных процессах, за счет низкочастотной точности.
Этот пример сравнивает методы устранения состояния команды balred, Truncate и MatchDC. Можно так же управлять методом устранения состояния в приложении Model Reducer, на вкладке Balanced Truncation, с помощью флажка Preserve DC Gain, как показано.

Рассмотрите следующую систему.

Создайте модель с обратной связью этой системы от r до y.
G = zpk([0 -2],[-1 -3],1); C = tf(2,[1 1e-2]); T = feedback(G*C,1)
T =
2 s (s+2)
--------------------------------
(s+0.004277) (s+1.588) (s+4.418)
Continuous-time zero/pole/gain model.
T является системой третьего порядка, которая имеет нулевую полюсом почти отмену близко к s = 0. Поэтому это - хороший кандидат на сокращение порядка приближением.
Вычислите два приближения второго порядка к T, тот, который сохраняет усиление DC и то, которое обрезает самое низкое энергетическое состояние, не изменяя другие состояния. Используйте balredOptions, чтобы задать методы приближения, MatchDC и Truncate, соответственно.
matchopt = balredOptions('StateElimMethod','MatchDC'); truncopt = balredOptions('StateElimMethod','Truncate'); Tmatch = balred(T,2,matchopt); Ttrunc = balred(T,2,truncopt);
Сравните частотные характеристики аппроксимированных моделей.
bodeplot(T,Tmatch,Ttrunc) legend('Original','DC Match','Truncate')

Усеченная модель Ttrunc совпадает с исходной моделью хорошо в высоких частотах, но значительно отличается в низкой частоте. С другой стороны Tmatch приводит к хорошему соответствию в низких частотах как ожидалось, за счет высокочастотной точности.
Можно также видеть различия между этими двумя методами путем исследования ответа временного интервала в различных режимах. Сравните медленную динамику путем рассмотрения переходного процесса всех трех моделей с долгосрочным горизонтом.
stepplot(T,Tmatch,'r--',Ttrunc,1500) legend('Original','DC Match','Truncate')

Как ожидалось, на долгом времени масштабирует соответствующее DC приближение, Tmatch имеет очень похожий ответ на исходную модель.
Сравните быстрые переходные процессы в переходном процессе.
stepplot(T,Tmatch,'r',Ttrunc,'g--',0.5) legend('Original','DC Match','Truncate')

В кратковременных шкалах усеченное приближение Ttrunc предоставляет лучшее соответствие исходной модели. Какой метод приближения, который необходимо использовать, зависит, на котором режим является самым важным для приложения.
Этот пример показывает, как вычислить приближение уменьшаемого порядка системы, когда система имеет нестабильные или почти нестабильные полюса.
При вычислении приближения уменьшаемого порядка команда balred (или приложение Model Reducer) не устраняет нестабильные полюса, потому что выполнение так существенно изменило бы системную динамику. Вместо этого программное обеспечение разлагает модель на стабильные и нестабильные части и уменьшает стабильную часть модели.
Если ваша модель имеет почти нестабильные полюса, вы можете хотеть гарантировать, что приближение уменьшаемого порядка сохраняет эти движущие силы. Этот пример показывает, как использовать опцию Offset balred, чтобы сохранить полюса, которые являются близко к стабильно-нестабильному контуру. Можно достигнуть того же результата в приложении Model Reducer, на вкладке Balanced Truncation, в соответствии с Опциями, с помощью поля Offset, как показано:

Загрузите модель с нестабильными и почти нестабильными полюсами.
load('reduce.mat','gasf35unst')
gasf35unst является моделью SISO с 25 состояниями с двумя нестабильными полюсами (Ре> 0). Исследуйте системные полюса, чтобы найти почти нестабильные полюса.
pzplot(gasf35unst) axis([-0.0015 0.0015 -0.0005 0.0005])

Нулевой полюсом график показывает несколько полюсов (отмеченный x) что падение левой полуплоскости, но относительно близко к мнимой оси. Это почти нестабильные полюса. Два из них находятся в пределах 0.0005 из нестабильности. Еще три находятся в пределах 0.001 из нестабильности.
Исследуйте график сингулярного значения Ганкеля модели.
hsvplot(gasf35unst)

График показывает два нестабильных режима, но вы не можете легко определить энергетический вклад почти нестабильных полюсов. В вашем приложении вы можете хотеть уменьшать модель, не отбрасывая те полюса, самые близкие к нестабильности, даже если они имеют относительно низкую энергию. Используйте опцию Offset balred, чтобы вычислить систему уменьшаемого порядка, которая сохраняет два стабильных полюса, которые являются самыми близкими к мнимой оси. Опция Offset устанавливает контур между полюсами, которые balred может отбросить, и полюса, которые balred должен сохранить (обработка как нестабильная).
opts = balredOptions('Offset',0.0005);
gasf_arr = balred(gasf35unst,[10 15],opts);При обеспечении balred, который заказывает массив целевого приближения, [10 15] заставляет balred возвращать массив аппроксимированных моделей. Массив gasf_arr содержит две модели, 10-й порядок и приближение 15-го порядка gasf35unst. В обоих приближениях balred не отбрасывает два нестабильных полюса или два почти нестабильных полюса.
Сравните приближения уменьшаемого порядка с исходной моделью.
bodeplot(gasf35unst,gasf_arr,'r--')
15-е приближение порядка является хорошим соответствием частотного диапазона к исходной модели. Однако приближение 10-го порядка показывает изменения в высокочастотной динамике, которая может быть слишком большой, чтобы быть приемлемой. Приближение 15-го порядка вероятно лучший выбор.
Фокусировка вычисления энергетического вклада на конкретной области частоты иногда приводит к хорошему приближению динамике интереса в низшем порядке, чем сокращение, которое принимает все частоты во внимание. В данном примере уменьшайте старшую модель с особым вниманием на динамике в конкретном интервале.
Этот пример демонстрирует ограниченное частотой сбалансированное усечение в командной строке, с помощью опций для команды balred. Можно также выполнить ограниченное частотой сбалансированное усечение в приложении Model Reducer, на вкладке Balanced Truncation, с помощью Избранного флажка частотного диапазона, как показано.

Загрузите модель и исследуйте ее частотную характеристику.
load(fullfile(matlabroot,'examples','control','build.mat'),'G') bodeplot(G)

G является моделью 48-го порядка с несколькими большими пиковыми областями приблизительно 5,2 рад/с, 13,5 рад/с и 24,5 рад/с, и меньшим peaks, рассеянным через многие частоты. Исследуйте график сингулярного значения Ганкеля видеть энергетические вклады состояний модели 48.
hsvd(G)

График сингулярного значения предполагает, что можно отбросить по крайней мере 20 состояний без существенного влияния на полный отклик системы. Предположим, что для вашего приложения вы только интересуетесь динамикой около второго большого пика между 10 рад/с и 22 рад/с. Попробуйте несколько порядков упрощенной модели на основе графика сингулярного значения Ганкеля. Сравните их частотные характеристики на исходную модель, особенно в области того пика.
G18 = balred(G,18); G10 = balred(G,10); bodeplot(G,G18,G10,logspace(0.5,1.5,100)); legend('Original','Order 18','Order 10');

Модель 18-го порядка является хорошим соответствием к динамике в видимой области. В 10-й модели порядка, однако, существует некоторое ухудшение соответствия.
Фокусируйте снижение сложности модели на видимой области, чтобы получить хорошее соответствие с приближением более низкоуровневым. Во-первых, исследуйте энергетические вклады состояния в той области частоты только. Используйте hsvdOptions, чтобы задать интервал частоты для hsvd.
hopt = hsvdOptions('FreqIntervals',[10,22]);
hsvd(G,hopt)
Сравнение этого графика к предыдущему графику сингулярного значения Ганкеля показывает, что в этой области частоты, много меньше состояний значительно способствует динамике, чем способствуют полной динамике.
Попробуйте те же порядки упрощенной модели снова, на этот раз выбрав состояния, чтобы устранить базирующийся только на их вкладе в интервал частоты. Используйте balredOptions, чтобы задать интервал частоты для balred.
bopt = balredOptions('StateElimMethod','Truncate','FreqIntervals',[10,22]); GLim18 = balred(G,18,bopt); GLim10 = balred(G,10,bopt); bodeplot(G,GLim18,GLim10,logspace(0.5,1.5,100)); legend('Original','Order 18','Order 10');

С ограниченным частотой энергетическим вычислением приближение 10-го порядка так хорошо в видимой области, как приближение 18-го порядка вычислило без пределов частоты.