Левинсон-Дербин

Решение систем линейных уравнений с помощью рекурсии Левинсона-Дербина

Библиотека

Математические функции / Матрицы и Линейная алгебра / Решатели Линейной системы

dspsolvers

Описание

Блок Левинсона-Дербина решает систему th-порядка n линейных уравнений

Ra = b

в случаях, где:

R является Эрмитовой, положительно-определенной, матрицей Теплица.
b идентичен первому столбцу R, переключенного одним элементом и с противоположным знаком.

$[\begin{matrix} r (1) & r^{*} (2) & \dots & r^{*} (n) \\ r (2) & r (1) & \dots & r^{*} (n - 1) \\ ⋮ & ⋮ & ⋱ & ⋮ \\ r (n) & r (n - 1) & \dots & r (1) \end{matrix}] [\begin{matrix} a (2) \\ a (3) \\ ⋮ \\ a (n + 1) \end{matrix}] = [\begin{matrix} - r (2) \\ - r (3) \\ ⋮ \\ - r (n + 1) \end{matrix}]$

Вход к блоку, r = [r(1) r(2) ... r(n+1)], может быть вектором или матрицей. Если вход является матрицей, блок обрабатывает каждый столбец как независимый канал и решает его отдельно. Каждый канал входа содержит, изолирует 0 через n последовательности автокорреляции, которые появляются в матричном R.

Блок может вывести полиномиальные коэффициенты, A, отражательные коэффициенты, K, и ошибочную степень прогноза, P, в различных комбинациях. Параметр Output(s) позволяет вам включать A и K выходные параметры путем выбора одной из следующих настроек:

A Для каждого канала портируйте выходные параметры A = [1 a(2) a(3) ... a(n+1)], решение уравнения Левинсона-Дербина. A имеет ту же размерность как вход. Можно также просмотреть элементы каждого выходного канала как коэффициенты th-порядка n, авторегрессивного (AR) процесс.
K Для каждого канала, порт K выходные параметры K = [k(1) k(2) ... k(n)], который содержит коэффициенты отражения n и имеет ту же размерность как вход, меньше одного элемента. Скалярный входной канал вызывает ошибку, когда вы выбираете K. Можно использовать отражательные коэффициенты, чтобы понять представление решетки процесса AR, описанного позже на этой странице.
A and K — Блок выходные параметры оба представления в их соответствующих портах. Скалярный входной канал вызывает ошибку, когда вы выбираете A and K.

Установите флажок Output prediction error power (P), чтобы вывести ошибочную степень прогноза для каждого канала, P. Для каждого канала P представляет степень вывода КИХ-фильтра с касаниями A и входная автокорреляция, описанная r, где A представляет ошибочный фильтр прогноза, и r является входом к блоку. В этом случае A является фильтром отбеливания. P имеет один элемент на входной канал.

Когда вы устанавливаете флажок If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0 (значение по умолчанию), входной канал, r которого элемент (1) является нулем, генерирует вывод с нулевым знаком. Когда вы снимаете этот флажок, вход с r (1) =, 0 генерирует NaN s в выводе. В целом вход с r (1) = 0 недопустим, потому что это не создает положительно-определенный матричный R. Часто, однако, блоки получают входные параметры с нулевым знаком в начале симуляции. Флажок позволяет вам стараться не распространять NaN s в этот период.

Приложения

Одно приложение формулировки Левинсона-Дербина, реализованной этим блоком, находится в проблеме Уокера Рождества АРА, которая касается моделирования неизвестной системы как авторегрессивный процесс. Вы смоделировали бы такой процесс как вывод БИХ-фильтра все-полюса с белым Гауссовым шумовым входом. В проблеме Уокера Рождества использование последовательности автокорреляции сигнала, чтобы получить оптимальную оценку приводит к a R = уравнение b типа, показанного выше, который наиболее эффективно решен рекурсией Левинсона-Дербина. В этом случае вход к блоку представляет последовательность автокорреляции с r(1), являющимся значением нулевой задержки. Вывод в блоке, порт затем содержит коэффициенты авторегрессивного процесса, который оптимально моделирует систему. Коэффициенты упорядочены в убывающих степенях z, и процесс AR является минимальной фазой. Ошибка прогноза, G, задает усиление для неизвестной системы, где $G = \sqrt{P}$ :

$H (z) = \frac{G}{A (z)} = \frac{G}{1 + a (2) z^{- 1} + ... + a (n + 1) z^{- n}}$

Вывод в порте K блока содержит соответствующие отражательные коэффициенты, [ k (1) k (2) ... k (n)], для реализации решетки этого БИХ-фильтра. Блок AR Estimator Уокера Рождества реализует этот основанный на автокорреляции метод для оценки модели AR, в то время как блок Method Уокера Рождества расширяет метод к спектральной оценке.

Другое распространенное приложение алгоритма Левинсона-Дербина находится в кодировании с линейным предсказанием, которое касается нахождения коэффициентов процесса скользящего среднего значения (MA) (или КИХ-фильтр), который предсказывает следующее значение сигнала от текущей выборки сигнала и конечного числа прошлых выборок. В этом случае вход к блоку представляет последовательность автокорреляции сигнала с r (1), являющийся значением нулевой задержки и выводом в блоке, порт содержит коэффициенты прогнозирующего процесса MA (в убывающих степенях z).

$H (z) = A (z) = 1 + a (2) z^{- 1} + ... a (n + 1) z^{- n}$

Эти коэффициенты решают следующую задачу оптимизации:

$\overset{\min}{{a_{i}}}$

$E [{| x_{n} - \sum_{i = 1}^{N} a_{i} x_{n - i} |}^{2}]$

Снова, вывод в порте K блока содержит соответствующие отражательные коэффициенты, [k(1) k(2) ... k(n)], для реализации решетки этого КИХ-фильтра. Блок Autocorrelation LPC в библиотеке Linear Prediction реализует этот основанный на автокорреляции метод прогноза.

Типы данных с фиксированной точкой

Схемы в этом разделе show типы данных, используемые в Левинсоне-Дербине, блокируются для сигналов фиксированной точки.

После инициализации блок выполняет обновления n. В (j +1) обновление,

$значение в аккумуляторе = r (j + 1) + \sum a_{j} (i) \times r (j - i + 1)$

Следующая схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

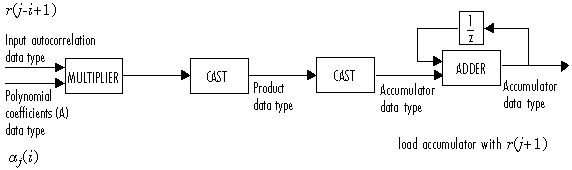
Блок затем обновляет отражательные коэффициенты K согласно

$K_{j + 1} = значение в аккумуляторе / P_{j}$

Блок затем обновляет ошибочную степень прогноза P согласно

$P_{j + 1} = P_{j} - P_{j} \times K_{j + 1} \times союз (K_{j + 1})$

Следующая схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

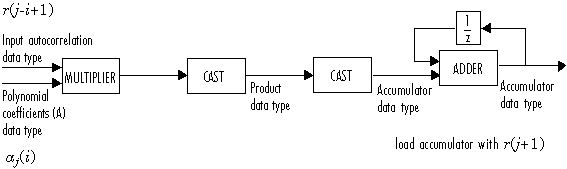
Полиномиальные коэффициенты A затем обновляются согласно

$a_{j + 1} (i) = a_{j} (i) + K_{j + 1} \times союз (_{aj} (j - 1 + i))$

Эта схема отображает типы данных с фиксированной точкой, используемые в этом вычислении:

Алгоритм

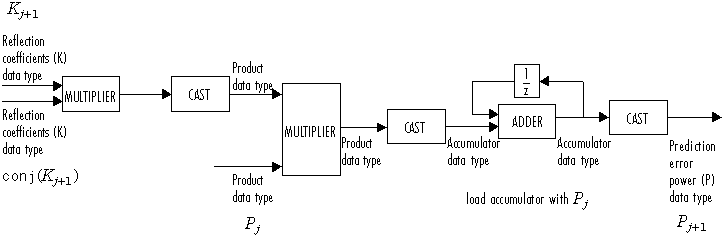
Алгоритм требует операций ^O(n2) для каждого входного канала. Эта реализация поэтому намного более эффективна для большого n, чем стандартное Исключение Гаусса, которое требует операций ^O(n3) на канал.

Параметры

Main Tab

Output(s)

Задайте представление решения R a = b, чтобы вывести: коэффициенты модели (A), отражательные коэффициенты (K), или оба (A and K). Когда вход является скалярным или вектором - строкой, необходимо установить этот параметр на A.

Output prediction error power (P)

Выберите, чтобы вывести ошибку прогноза в порте P.

If the value of lag 0 is zero, A=[1 zeros], K=[zeros], P=0

Когда вы устанавливаете этот флажок, и первый элемент входа, r(1), является нулем, блок выводит следующие векторы, как соответствующие:

A = [1 zeros(1,n)]
K = [zeros(1,n)]
P = 0

Когда вы снимаете этот флажок, блок выводит вектор NaN s для каждого канала, элемент r(1) которого является нулем.

Data Types Tab

Примечание

Наследование с плавающей точкой более приоритетно по сравнению с настройками типа данных, заданными на этой панели. Когда входные параметры являются плавающей точкой, блок игнорирует эти настройки, и все внутренние типы данных являются плавающей точкой.

Rounding mode

Задайте округляющийся режим для операций фиксированной точки как одно из следующего:

Floor
Ceiling
Convergent
Nearest
Round
Simplest
Zero

Для получения дополнительной информации смотрите округление режима.

Saturate on integer overflow

Когда вы выбираете этот параметр, блок насыщает результат своей операции фиксированной точки. Когда вы очищаете этот параметр, блок переносит результат своей операции фиксированной точки. Для получения дополнительной информации на saturate и wrap, смотрите режим переполнения для операций фиксированной точки.

Product output

Задайте тип выходных данных продукта. Смотрите Типы данных с фиксированной точкой и Типы данных Умножения для рисунков, изображающих использование типа выходных данных продукта в этом блоке. Можно установить его на:

Правило, которое наследовало тип данных, например, Inherit: Same as input
Выражение, которое оценивает к допустимому типу данных, например, fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, который помогает вам установить параметр Product output.

Смотрите Задают Типы данных Используя Ассистент Типа данных (Simulink) для получения дополнительной информации.

Accumulator

Задайте тип данных аккумулятора. Смотрите Типы данных с фиксированной точкой для рисунков, изображающих использование типа данных аккумулятора в этом блоке. Можно установить его на:

Правило, которое наследовало тип данных, например, Inherit: Same as input
Правило, которое наследовало тип данных, например, Inherit: Same as product output
Выражение, которое оценивает к допустимому типу данных, например, fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, который помогает вам установить параметр Accumulator.

Смотрите Задают Типы данных Используя Ассистент Типа данных (Simulink) для получения дополнительной информации.

Polynomial coefficients (A)

Задайте полиномиальные коэффициенты (A) тип данных. Смотрите Типы данных с фиксированной точкой для рисунков, изображающих использование тип данных в этом блоке. Можно установить его на выражение, которое оценивает к допустимому типу данных, например, fixdt(1,16,15).

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, который помогает вам установить параметр A.

Смотрите Задают Типы данных Используя Ассистент Типа данных (Simulink) для получения дополнительной информации.

Reflection coefficients (K)

Задайте полиномиальные коэффициенты (A) тип данных. Смотрите Типы данных с фиксированной точкой для рисунков, изображающих использование типа данных K в этом блоке. Можно установить его на выражение, которое оценивает к допустимому типу данных, например, fixdt(1,16,15).

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, который помогает вам установить параметр K.

Смотрите Задают Типы данных Используя Ассистент Типа данных (Simulink) для получения дополнительной информации.

Prediction error power (P)

Задайте ошибочную степень прогноза (P) тип данных. Смотрите Типы данных с фиксированной точкой для рисунков, изображающих использование типа данных P в этом блоке. Можно установить его на:

Правило, которое наследовало тип данных, например, Inherit: Same as input
Выражение, которое оценивает к допустимому типу данных, например, fixdt(1,16,0)

Нажмите кнопку Show data type assistant, чтобы отобразить Data Type Assistant, который помогает вам установить параметр P.

Смотрите Задают Типы данных Используя Ассистент Типа данных (Simulink) для получения дополнительной информации.

Minimum

Задайте минимальные значения, которые должны иметь полиномиальные коэффициенты, отражательные коэффициенты или ошибочная степень прогноза. Значением по умолчанию является [], который (незаданный).Simulink^® использует это значение, чтобы выполнить:

Проверка диапазона параметра (см., Задает Минимальные и Максимальные значения для Параметров блоков (Simulink)),
Автоматическое масштабирование типов данных с фиксированной точкой

Maximum

Задайте максимальные значения, которые должны иметь полиномиальные коэффициенты, отражательные коэффициенты или ошибочная степень прогноза. Значением по умолчанию является (незаданный) []. Simulink использует это значение, чтобы выполнить:

Проверка диапазона параметра (см., Задает Минимальные и Максимальные значения для Параметров блоков (Simulink)),
Автоматическое масштабирование типов данных с фиксированной точкой

Lock data type settings against changes by the fixed-point tools

Выберите этот параметр, чтобы препятствовать тому, чтобы Fixed-Point Tool заменили типы данных, которые вы задаете на маске блока.

Ссылки

Golub, G. H. и К. Ф. ван Лоун. Секта. 4.7 в Матричных Вычислениях. 3-й редактор Балтимор, MD: Johns Hopkins University Press, 1996.

Ljung, L. System Identification: теория для пользователя. Englewood Cliffs, NJ: Prentice Hall, 1987. PGS. 278–280.

Кей, Стивен М. Современная спектральная оценка: теория и приложение. Englewood Cliffs, NJ: Prentice Hall, 1988.

Поддерживаемые типы данных

Плавающая точка двойной точности
Плавающая точка с одинарной точностью
Фиксированная точка (подписался только),
8-, 16-, и 32-битные целые числа со знаком

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью Simulink® Coder™.

Сгенерированный код полагается на memcpy или функции memset (string.h) при определенных обстоятельствах.

Преобразование фиксированной точки
Преобразуйте алгоритмы с плавающей точкой в фиксированную точку с помощью Fixed-Point Designer™.

Если вход является фиксированной точкой, это должно быть целое число со знаком или подписанная фиксированная точка с наклоном степени двойки и нулевым смещением.

Смотрите также

Функции

levinson

Блоки

LPC автокорреляции | Решатель Холесского | Решатель LDL | Решатель LU | Решатель QR | Средство оценки AR Уокера Рождества | Метод Уокера Рождества

Документация

Левинсон-Дербин

Библиотека