прогноз
Класс: regARIMA
Предскажите ответы модели регрессии с ошибками ARIMA
Синтаксис
[Y,YMSE]
= forecast(Mdl,numperiods)
[Y,YMSE,U]
= forecast(Mdl,numperiods)
[Y,YMSE,U]
= forecast(Mdl,numperiods,Name,Value)
Описание
[ ответы прогнозов (Y,YMSE]
= forecast(Mdl,numperiods)Y) для модели регрессии с ошибками временных рядов ARIMA и генерируют соответствующие среднеквадратичные погрешности (YMSE).
[ дополнительно предсказывает безусловные воздействия для модели регрессии с ошибками ARIMA.Y,YMSE,U]
= forecast(Mdl,numperiods)
[ прогнозы с дополнительными опциями, заданными одним или несколькими аргументами пары Y,YMSE,U]
= forecast(Mdl,numperiods,Name,Value)Name,Value.
Входные параметры
Выходные аргументы
Примеры
Предскажите ответы модели регрессии с ошибками ARIMA
Предскажите ответы из следующей модели регрессии с ARMA (2,1) ошибки по горизонту с 30 периодами:
где является Гауссовым с отклонением 0.1.
Задайте модель. Моделируйте ответы из модели и двух рядов предиктора.
Mdl = regARIMA('Intercept',0,'AR',{0.5 -0.8},... 'MA',-0.5,'Beta',[0.1 -0.2],'Variance',0.1); rng(1); % For reproducibility X = randn(130,2); y = simulate(Mdl,130,'X',X);
Соответствуйте модели к первым 100 наблюдениям и зарезервируйте остающиеся 30 наблюдений, чтобы оценить производительность прогноза.
ToEstMdl = regARIMA('ARLags',1:2); EstMdl = estimate(ToEstMdl,y(1:100),'X',X(1:100,:));
Regression with ARMA(2,0) Error Model (Gaussian Distribution):
Value StandardError TStatistic PValue
________ _____________ __________ __________
Intercept 0.004358 0.021314 0.20446 0.83799
AR{1} 0.36833 0.067103 5.4891 4.0408e-08
AR{2} -0.75063 0.090865 -8.2609 1.4453e-16
Beta(1) 0.076398 0.023008 3.3205 0.00089863
Beta(2) -0.1396 0.023298 -5.9919 2.0741e-09
Variance 0.079876 0.01342 5.9522 2.6453e-09
[yF,yMSE] = forecast(EstMdl,30,'Y0',y(1:100),... 'X0',X(1:100,:),'XF',X(101:end,:));
EstMdl является новой моделью regARIMA, содержащей оценки. Оценки близко к их истинным значениям.
Используйте EstMdl, чтобы предсказать горизонт с 30 периодами. Визуально сравните прогнозы с данными о затяжке с помощью графика.
[yF,yMSE] = forecast(EstMdl,30,'Y0',y(1:100),... 'X0',X(1:100,:),'XF',X(101:end,:)); figure plot(y,'Color',[.7,.7,.7]); hold on plot(101:130,yF,'b','LineWidth',2); plot(101:130,yF+1.96*sqrt(yMSE),'r:',... 'LineWidth',2); plot(101:130,yF-1.96*sqrt(yMSE),'r:','LineWidth',2); h = gca; ph = patch([repmat(101,1,2) repmat(130,1,2)],... [h.YLim fliplr(h.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend('Observed','Forecast',... '95% Forecast Interval','Location','Best'); title(['30-Period Forecasts and Approximate 95% '... 'Forecast Intervals']) axis tight hold off
Много наблюдений в демонстрационном падении затяжки вне 95%-х интервалов прогноза. Две причины этого:
Предикторы случайным образом сгенерированы в этом примере.
estimateобрабатывает предикторы, как зафиксировано. Впоследствии, 95%-е интервалы прогноза на основе оценок отestimateне составляют изменчивость в предикторах.Шансом сдвига период оценки кажется менее энергозависимым, чем период прогноза.
estimateиспользует менее энергозависимые данные о периоде оценки, чтобы оценить параметры. Поэтому предскажите, что интервалы на основе оценок не должны покрывать наблюдения, которые имеют базовый инновационный процесс с большей изменчивостью.
Предскажите GDP Используя модель регрессии с ошибками ARMA
Предскажите стационарный, регистрируйте GDP с помощью модели регрессии с ARMA (1,1) ошибки, включая CPI как предиктор.
Загрузите американский макроэкономический набор данных и предварительно обработайте данные.
load Data_USEconModel; logGDP = log(DataTable.GDP); dlogGDP = diff(logGDP); % For stationarity dCPI = diff(DataTable.CPIAUCSL); % For stationarity numObs = length(dlogGDP); gdp = dlogGDP(1:end-15); % Estimation sample cpi = dCPI(1:end-15); T = length(gdp); % Effective sample size frstHzn = T+1:numObs; % Forecast horizon hoCPI = dCPI(frstHzn); % Holdout sample dts = dates(2:end); % Date nummbers
Соответствуйте модели регрессии ARMA (1,1) ошибки.
ToEstMdl = regARIMA('ARLags',1,'MALags',1); EstMdl = estimate(ToEstMdl,gdp,'X',cpi);
Regression with ARMA(1,1) Error Model (Gaussian Distribution):
Value StandardError TStatistic PValue
__________ _____________ __________ __________
Intercept 0.014793 0.0016289 9.0818 1.0684e-19
AR{1} 0.57601 0.10009 5.7548 8.6754e-09
MA{1} -0.15258 0.11978 -1.2738 0.20272
Beta(1) 0.0028972 0.0013989 2.071 0.038355
Variance 9.5734e-05 6.5562e-06 14.602 2.723e-48
Предскажите уровень GDP по 15 горизонтам четверти. Используйте выборку оценки в качестве предварительной выборки для прогноза.
[gdpF,gdpMSE] = forecast(EstMdl,15,'Y0',gdp,... 'X0',cpi,'XF',hoCPI);
Постройте прогнозы и 95%-е интервалы прогноза.
figure h1 = plot(dts(end-65:end),dlogGDP(end-65:end),... 'Color',[.7,.7,.7]); datetick hold on h2 = plot(dts(frstHzn),gdpF,'b','LineWidth',2); h3 = plot(dts(frstHzn),gdpF+1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); plot(dts(frstHzn),gdpF-1.96*sqrt(gdpMSE),'r:','LineWidth',2); ha = gca; title(['{\bf Forecasts and Approximate 95% }'... '{\bf Forecast Intervals for GDP rate}']); ph = patch([repmat(dts(frstHzn(1)),1,2) repmat(dts(frstHzn(end)),1,2)],... [ha.YLim fliplr(ha.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend([h1 h2 h3],{'Observed GDP rate','Forecasted GDP rate ',... '95% Forecast Interval'},'Location','Best','AutoUpdate','off'); axis tight hold off
Предскажите Используя модель регрессии с ошибками ARIMA и известным прерыванием
Предскажите модульный неустановившийся корень, регистрируйте GDP с помощью модели регрессии с ARIMA (1,1,1) ошибки, включая CPI как предиктор и известное прерывание.
Загрузите американский Макроэкономический набор данных и предварительно обработайте данные.
load Data_USEconModel; numObs = length(DataTable.GDP); logGDP = log(DataTable.GDP(1:end-15)); cpi = DataTable.CPIAUCSL(1:end-15); T = length(logGDP); % Effective sample size frstHzn = T+1:numObs; % Forecast horizon hoCPI = DataTable.CPIAUCSL(frstHzn); % Holdout sample
Задайте модель в течение периода оценки.
ToEstMdl = regARIMA('ARLags',1,'MALags',1,'D',1);
Прерывание не идентифицируется в модели с интегрированными ошибками, поэтому зафиксируйте ее значение перед оценкой. Один способ сделать это должно оценить прерывание с помощью простой линейной регрессии.
Reg4Int = [ones(T,1), cpi]\logGDP; intercept = Reg4Int(1);
Рассмотрите выполнение анализа чувствительности при помощи сетки прерываний.
Установите прерывание и соответствуйте модели регрессии ARIMA (1,1,1) ошибки.
ToEstMdl.Intercept = intercept; EstMdl = estimate(ToEstMdl,logGDP,'X',cpi,... 'Display','off')
EstMdl =
regARIMA with properties:
Description: "ARIMA(1,1,1) Error Model (Gaussian Distribution)"
Distribution: Name = "Gaussian"
Intercept: 5.80142
Beta: [0.00396705]
P: 2
D: 1
Q: 1
AR: {0.922709} at lag [1]
SAR: {}
MA: {-0.387846} at lag [1]
SMA: {}
Variance: 0.000108943
Regression with ARIMA(1,1,1) Error Model (Gaussian Distribution)
Предскажите GDP по 15 горизонтам четверти. Используйте выборку оценки в качестве предварительной выборки для прогноза.
[gdpF,gdpMSE] = forecast(EstMdl,15,'Y0',logGDP,... 'X0',cpi,'XF',hoCPI);
Постройте прогнозы и 95%-е интервалы прогноза.
figure h1 = plot(dates(end-65:end),log(DataTable.GDP(end-65:end)),... 'Color',[.7,.7,.7]); datetick hold on h2 = plot(dates(frstHzn),gdpF,'b','LineWidth',2); h3 = plot(dates(frstHzn),gdpF+1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); plot(dates(frstHzn),gdpF-1.96*sqrt(gdpMSE),'r:',... 'LineWidth',2); ha = gca; title(['{\bf Forecasts and Approximate 95% }'... '{\bf Forecast Intervals for log GDP}']); ph = patch([repmat(dates(frstHzn(1)),1,2) repmat(dates(frstHzn(end)),1,2)],... [ha.YLim fliplr(ha.YLim)],... [0 0 0 0],'b'); ph.FaceAlpha = 0.1; legend([h1 h2 h3],{'Observed GDP','Forecasted GDP',... '95% Forecast Interval'},'Location','Best','AutoUpdate','off'); axis tight hold off
Безусловные воздействия, , являются неустановившимися, поэтому ширины интервалов прогноза растут со временем.
Больше о
Базовые разделы времени для прогнозирования
Time base partitions for forecasting является двумя непересекающимися, непрерывными интервалами основы времени; каждый интервал содержит данные временных рядов для прогнозирования динамической модели. forecast period (горизонт прогноза) является разделом длины numperiods в конце основы времени, во время которой forecast генерирует, предсказывает Y от динамической модели Mdl. presample period является целым разделом, происходящим перед периодом прогноза. forecast может потребовать, чтобы наблюдаемые ответы Y0, данные о регрессии X0, безусловные воздействия U0 или инновации E0 в преддемонстрационный период инициализировали динамическую модель для прогнозирования. Образцовая структура определяет типы и объемы необходимых преддемонстрационных наблюдений.
Установившаяся практика должна соответствовать динамической модели к фрагменту набора данных, затем подтвердить предсказуемость модели путем сравнения ее прогнозов с наблюдаемыми ответами. Во время прогнозирования преддемонстрационный период содержит данные, к которым модель является подходящей, и период прогноза содержит выборку затяжки для валидации. Предположим, что yt является наблюдаемым рядом ответа; x 1, t, x 2, t и x 3, t наблюдается внешний ряд; и время t = 1, …, T. Рассмотрите ответы прогнозирования от динамической модели y t содержащий компонент регрессии numperiods = периоды K. Предположим, что динамическая модель является подходящей к данным в интервале [1, T – K] (для получения дополнительной информации, смотрите estimate). Эти данные показывают базовые разделы времени для прогнозирования.
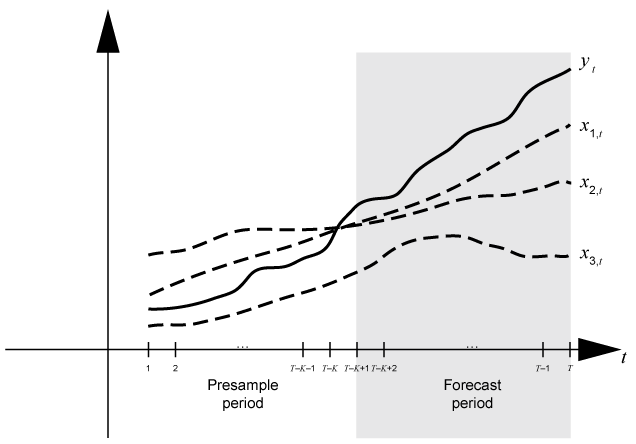
Например, сгенерировать предсказывает Y из модели регрессии с AR (2) ошибки, forecast требует преддемонстрационных безусловных воздействий U0 и будущие данные о предикторе XF.
forecastвыводит безусловные воздействия, учитывая достаточные легко доступные преддемонстрационные ответы и данные о предикторе. Инициализировать AR (2) ошибочная модель,Y0= иX0= .К модели
forecastтребует будущих внешних данныхXF= .
Эти данные показывают массивы необходимых наблюдений для общего случая с соответствующими аргументами ввода и вывода.
Алгоритмы
forecastвычисляет предсказанный ответ MSEs,YMSE, путем обработки матриц данных о предикторе (X0иXF) как нестохастических и статистически независимых от образцовых инноваций. ПоэтомуYMSEотражает отклонение, сопоставленное с безусловными воздействиями одной только ошибочной модели ARIMA.forecastиспользуетY0иX0, чтобы вывестиU0. Поэтому, если вы задаетеU0,forecastигнорируетY0иX0.
Ссылки
[1] Поле, G. E. P. Г. М. Дженкинс и Г. К. Рейнсель. Анализ timeseries: Прогнозирование и Управление. 3-й редактор Englewood Cliffs, NJ: Prentice Hall, 1994.
[2] Дэвидсон, R. и Дж. Г. Маккиннон. Эконометрическая теория и методы. Оксфорд, Великобритания: Издательство Оксфордского университета, 2004.
[3] Enders, W. Прикладные эконометрические временные ряды. Хобокен, NJ: John Wiley & Sons, Inc., 1995.
[4] Гамильтон, J. D. Анализ timeseries. Принстон, NJ: Издательство Принстонского университета, 1994.
[5] Pankratz, A. Прогнозирование с моделями динамической регрессии. John Wiley & Sons, Inc., 1991.
[6] Tsay, R. S. Анализ Финансовых Временных рядов. 2-й редактор Хобокен, NJ: John Wiley & Sons, Inc., 2005.