Exponenta Banner

h2hinfsyn

Смешанный H 2/H ∞ синтез с региональными ограничениями размещения полюса

свернуть все на странице

Синтаксис

[K,CL,normz,info] = h2hinfsyn(P,Nmeas,Ncon,Nz2,Wz,Name,Value)

Описание

пример

[K,CL,normz,info] = h2hinfsyn(P,Nmeas,Ncon,Nz2,Wz,Name,Value) использует методы LMI, чтобы вычислить закон выходного управления с обратной связью u = K (s) y для проблемы управления следующего рисунка.

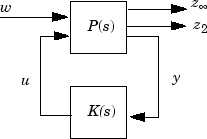
Объект LTI P разделил форму пространства состояний, данную

x˙=Ax+B1w+B2u,z∞=C1x+D11w+D12u,z2=C2x+D21w+D22u,y=Cyx+Dy1w+Dy2u.

Получившийся контроллер K:

  • Сохраняет H ∞ нормой G передаточной функции от w до z ∞ ниже значения, вы задаете использование аргумента Name,Value 'HINFMAX'.

  • Сохраняет H 2 нормами H передаточной функции от w до z 2 ниже значения, вы задаете использование аргумента Name,Value 'H2MAX'.

  • Минимизирует критерий компромисса формы

    W1G2+W2H2,

    где W 1 и W 2 является первыми и вторыми записями в векторном Wz.

  • Помещает полюса с обратной связью в область LMI, что вы задаете использование аргумента Name,Value 'REGION'.

Используйте входные параметры Nmeas, Ncon и Nz2, чтобы задать количество сигналов в y, u и z 2, соответственно. Можно использовать дополнительные пары Name,Value, чтобы задать дополнительные опции для вычисления.

Примеры

свернуть все

Скрипт Open Live Script

Учитывая объект, разработайте контроллер, таким образом, что полюса системы с обратной связью лежат в полуплоскости, заданной Ре <–1.

Можно задать эту область для размещения полюса с помощью интерактивной команды lmireg. Для этого

  1. Введите region = lmireg в командной строке MATLAB®.

  2. Введите h, чтобы задать ограничение полуплоскости.

  3. Введите l, чтобы задать левую полуплоскость.

  4. Введите -1, чтобы указать, что сокращением для области является x0 = –1.

  5. Введите q, чтобы выйти и создать область LMI.

Область, созданная этим процессом, эквивалентна следующим командам. (Для получения дополнительной информации смотрите страницу с описанием lmireg.) 

RealPart = -1; 
region = [-2*RealPart + 1i 1];

Задайте модель объекта управления. В данном примере используйте с тремя входами, 2D вывод разделил объект. 

A = [1 0;2 1]; 
B = [1 1;1 0]; 
C = [1 1;1 1;1 1]; 
D = zeros(3,2);
P = ss(A,B,C,D);

Вычислите контроллер для P с помощью области LMI, чтобы ограничить местоположения полюса с обратной связью. Примите, что разделенный объект содержит один управляющий сигнал и один сигнал измерения (nmeas = ncont = 1). Применяйтесь H2 ограничение нормы к одному сигналу (Nz2 = 1), и дает H2 и H∞ нормы равняются весу. 

ncont = 1;
nmeas = 1;
Nz2 = 1 ;
Wz = [0 0];
[K,CL] = h2hinfsyn(P,nmeas,ncont,Nz2,Wz,'Region',region); 
 Solver for LMI feasibility problems L(x) < R(x)
    This solver minimizes  t  subject to  L(x) < R(x) + t*I
    The best value of t should be negative for feasibility

 Iteration   :    Best value of t so far 
 
     1                        7.368392
     2                      -95.362851

 Result:  best value of t:   -95.362851
          f-radius saturation:  0.009% of R =  1.00e+08

Подтвердите, что полюса системы с обратной связью имеют Ре <–1. 

pole(CL)
ans = 4×1 complex

  -1.6786 + 3.2056i
  -1.6786 - 3.2056i
  -1.5563 + 1.6678i
  -1.5563 - 1.6678i

Можно продвинуть собственные значения с обратной связью, дальнейшие оставленный путем изменения RealPart. Или можно задать другие области размещения полюса. Например, поместите полюса, таким образом, что Ре падает в полосе комплексной плоскости –5 <Ре <–3. Чтобы задать эту область, используйте lmireg в интерактивном режиме, чтобы создать Ре определения reg1> –5 и Ре определения reg2 <–3. Затем введите region = lmireg(reg1,reg2), чтобы задать пересечение этих двух областей. Следующий код эквивалентен. 

LeftRealPart = -5; 
RightRealPart = -3;
region = [-2*RightRealPart + 1i 0 1 0;
           0 2*LeftRealPart + 1i 0 -1];

Вычислите новый контроллер и подтвердите местоположения полюсов с обратной связью.

[K,CL] = h2hinfsyn(P,nmeas,ncont,Nz2,Wz,'Region',region); 
 Solver for LMI feasibility problems L(x) < R(x)
    This solver minimizes  t  subject to  L(x) < R(x) + t*I
    The best value of t should be negative for feasibility

 Iteration   :    Best value of t so far 
 
     1                       17.688394
     2                        1.074621
     3                      -13.502955

 Result:  best value of t:   -13.502955
          f-radius saturation:  0.048% of R =  1.00e+08
 

pole(CL)
ans = 4×1 complex

  -3.7864 + 4.9210i
  -3.7864 - 4.9210i
  -3.7752 + 3.6186i
  -3.7752 - 3.6186i

Входные параметры

свернуть все

Объект, заданный как модель LTI, такая как модель tf или ss. P должен быть непрерывно-разовой моделью.

Количество сигналов измерения, заданных как положительное целое число. Это значение является количеством сигналов в y.

Количество управляющих сигналов, заданных как положительное целое число. Это значение является количеством сигналов в u.

Количество сигналов подвергает ограничению на H 2 нормы, заданные как положительное целое число. Это значение является количеством сигналов в z 2. Если общим количеством выходных параметров P является Nout, то первый Nout - Nz2 - Nmeas выходные параметры P подвергается ограничению на H ∞ норма.

Веса для H ∞ и H 2 производительности, заданная как 1 2 вектор формы [Winf,W2].

Аргументы в виде пар имя-значение

Укажите необязательные аргументы в виде пар ""имя, значение"", разделенных запятыми. Имя (Name) — это имя аргумента, а значение (Value) — соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: 'REGION',reg,'H2MAX',1,'HINFMAX',1,'DISPLAY','on'

Область размещения полюса, заданная как пара, разделенная запятой, состоящая из 'REGION' и матрица формы [L,M]. Эта матрица задает область размещения полюса как:

{z:L+zM+z¯MT<0}.

Сгенерируйте матрицу с помощью lmireg. Область LMI по умолчанию для размещения полюса, заданного пустым матричным [], является открытой левой полуплоскостью, осуществляя устойчивость с обратной связью только.

Верхняя граница на H 2 нормы передаточной функции от w до z 2, заданный как пара, разделенная запятой, состоящая из 'H2MAX' и значения положительной скалярной величины или Inf. Значение по умолчанию Inf эквивалентен обнулению предела и заставляет h2hinfsyn минимизировать H 2 нормы, подвергающиеся критерию компромисса.

Пример: 'H2MAX',1

Верхняя граница на H ∞ норма передаточной функции от w до z ∞, заданный как пара, разделенная запятой, состоящая из 'HINFMAX' и значения положительной скалярной величины или Inf. Значение по умолчанию Inf эквивалентен обнулению предела и заставляет h2hinfsyn минимизировать H ∞ норма, подвергающаяся критерию компромисса.

Пример: 'HINFMAX',1

Привязанный норма по проходному матричному DK контроллера, заданного как пара, разделенная запятой, состоящая из 'DKMAX' и неотрицательного скалярного значения. Сделать контроллер K строго соответствующий, набор 'DKMAX' к 0.

Пример: 'DKMAX',0

Желаемая относительная точность на оптимальном значении критерия компромисса, заданного как пара, разделенная запятой, состоящая из 'TOL' и значения положительной скалярной величины.

Переключитесь для отображения на экране информации синтеза, указанной как пара, разделенная запятой, состоящая из 'DISPLAY' и или 'on' или 'off'.

Выходные аргументы

свернуть все

Оптимальный контроллер выходной обратной связи, возвращенный как модель (ss) пространства состояний с входными параметрами Nmeas и Ncon выходные параметры.

Система с обратной связью с синтезируемым контроллером, возвращенным как модель (ss) пространства состояний. Системой с обратной связью является CL = lft(P,K).

Нормы с обратной связью, возвращенные как 1 2 вектор. Записи в этом векторе, соответственно:

  • H ∞ норма передаточной функции с обратной связью от w до z ∞.

  • H 2 нормы передаточной функции с обратной связью от w до z 2.

Решения условий разрешимости LMI, возвращенных как структура, содержащая следующие поля:

  • R Решение R условия разрешимости LMI

  • S Решение S условия разрешимости LMI

Ссылки

[1] Chilali, M. и П. Гэхинет, “H ∞ Проект с Ограничениями Размещения полюса: Подход LMI”, Противоречие AUT Сделки IEEE, 41 (1995), стр 358–367.

[2] Scherer, C., “Смешанный H2/H-infinity Управление”, Тренды в Управлении: европейская Перспектива, Springer-Verlag (1995), pp.173–216.

Смотрите также

|

Представлено до R2006a

Документация Robust Control Toolbox
Поддержка