H ∞ настройка контроллеров фиксированной структуры
CL = hinfstruct(CL0)
[CL,gamma,info]
= hinfstruct(CL0)
[CL,gamma,info]
= hinfstruct(CL0,options)
[C,gamma,info]
= hinfstruct(P,C0,options)
CL = hinfstruct(CL0)genss CL0. Эта настройка минимизирует H ∞ норма передаточной функции с обратной связью, смоделированной CL0. Модель CL0 представляет систему управления с обратной связью, которая включает настраиваемые компоненты, такие как контроллеры или фильтры. CL0 может также включать функции взвешивания то получение конструктивные требования.
[ возвращает CL,gamma,info]
= hinfstruct(CL0)gamma (минимальный H ∞ норма) и структура данных info с дополнительной информацией о каждой запущенной оптимизации.
[ позволяет вам задавать дополнительные опции для оптимизатора с помощью CL,gamma,info]
= hinfstruct(CL0,options)hinfstructOptions.
[ настраивается параметрический контроллер блокирует C,gamma,info]
= hinfstruct(P,C0,options)C0. Эта настройка минимизирует H ∞ норма системы с обратной связью CL0 = lft(P,C0). Чтобы использовать этот синтаксис, выразите свою систему управления и конструктивные требования как модель Standard Form, как на следующем рисунке:
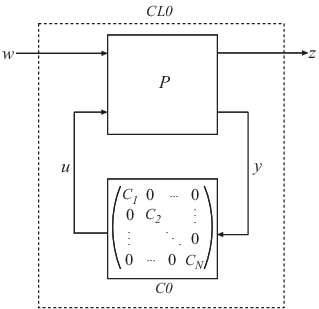
P является числовой моделью LTI, которая включает фиксированные элементы архитектуры управления. P может также включать функции взвешивания то получение конструктивные требования. C0 может быть одним настраиваемым компонентом (например, Блок Системы управления (Control System Toolbox) или модель genss) или массив ячеек нескольких настраиваемых компонентов. C является параметрической моделью или массивом параметрических моделей тех же типов как C0.
|
Обобщенная модель (
|
|
Числовая модель LTI, представляющая фиксированные элементы архитектуры управления, которая будет настроена.
|
|
Один настраиваемый или массив ячеек компонента настраиваемых компонентов управляющей структуры. Каждая запись в Для получения дополнительной информации и примеры создания настраиваемых моделей, см. Модели с Настраиваемыми Коэффициентами (Control System Toolbox) в Руководстве пользователя Control System Toolbox™.
|
|
Набор опций для |
|
Настроенная версия обобщенной модели ( Команда Чтобы получить доступ к настроенным значениям параметров, используйте |
|
Настроенные версии параметрических моделей Когда Когда |
|
Лучше всего достигнутое значение для H с обратной связью ∞ норма. В некоторых случаях |
|
Массив структуры данных, содержащий результаты каждой запущенной оптимизации. Поля
|
hinfstruct связан с hinfsyn, который также использует H ∞ методы, чтобы разработать контроллер для объекта MIMO. Однако различающийся hinfstruct, hinfsyn не вводит ограничения для структуры и порядка контроллера. По этой причине hinfsyn всегда возвращает меньший gamma, чем hinfstruct. Можно поэтому использовать hinfsyn, чтобы получить нижнюю границу на лучшей достижимой производительности.
Используя hinfstruct требует некоторого знакомства с H ∞ методы. Это требует выражения ваших конструктивных требований как функции взвешивания частоты на вводах и выводах объекта, как описано в Формулировке Конструктивных требований как Ограничения H-бесконечности. Для более простого подхода к настройке фиксированной структуры используйте systune или looptune.
Использование hinfstruct специализированные несглаженные методы оптимизации, чтобы осуществить устойчивость с обратной связью и минимизировать H ∞ норма как функция настраиваемых параметров. Эти методы основаны на работе в [1].
hinfstruct вычисляет норму H∞ с помощью алгоритма [2] и сохранение структуры eigensolvers от библиотеки SLICOT. Для получения дополнительной информации о библиотеке SLICOT, см. http://slicot.org.
[1] П. Апкэриэн и Д. Нолл, "Несглаженный Синтез H-бесконечности", Транзакции IEEE на Автоматическом управлении, Издании 51, Номере 1, 2006, стр 71-86.
[2] Bruisma, Н.Э. и М. Стейнбач, "Алгоритм FAST, чтобы Вычислить -норму H Матрицы Передаточной функции", Системные Буквы Управления, 14 (1990), стр 287-293.
genss | getValue | hinfstructOptions | hinfsyn | looptune | systune