mtaylorВычислите многомерное расширение Ряда Тейлора
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
mtaylor(f,x = x0, <order>, <mode>, <weights>, <Mapcoeffs = mc>) mtaylor(f,x, <order>, <mode>, <weights>, <Mapcoeffs = mc>) mtaylor(f,x = x0,AbsoluteOrder = order, <weights>, <Mapcoeffs = mc>) mtaylor(f,x = x0,RelativeOrder = order, <weights>, <Mapcoeffs = mc>) mtaylor(f,[x = x0, y = y0, …], <order>, <mode>, <weights>, <Mapcoeffs = mc>) mtaylor(f,[x, y, …], <order>, <mode>, <weights>, <Mapcoeffs = mc>) mtaylor(f,[x = x0, y = y0, …], <AbsoluteOrder = order>, <weights>, <Mapcoeffs = mc>) mtaylor(f,[x = x0, y = y0, …],RelativeOrder = order, <weights>, <Mapcoeffs = mc>)
mtaylor(f, [x = x0, y = y0, ...]) вычисляет первые сроки многомерного Ряда Тейлора f относительно переменных x, y и т.д. вокруг точек x = x0, y = y0 и т.д.
С режимом по умолчанию RelativeOrder количество требуемых условий для расширения определяется order, если задано. Если никакой порядок не задан, значение переменной окружения, ORDER используется. Можно изменить значение по умолчанию 6 путем присвоения нового значения ORDER.
Условия считаются от самой низкой общей степени на для конечных точек расширения, и от самого высокого общего термина степени на для расширений вокруг бесконечности.
Если AbsoluteOrder задан, order представляет порядок усечения ряда, т.е. никакие условия общей степени order или выше вычисляется.
Для бесконечных точек расширения абсолютные значения экспонент соответствующих переменных используются, чтобы вычислить общую степень.
Поскольку конечное расширение указывает x0, y0, ..., вычисленный ряд относительно переменных x, y, ... веса, w1, w2, ...
taylor(f(x0 + t^w1*(x - x0), y0 + t^w2*(y - y0), dots), t = 0),
оцененный в точке t = 1.
Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных вычислениях.
Мы вычисляем Ряд Тейлора вокруг источника (значение по умолчанию). Расширение содержит все условия через общую степень 3:
mtaylor(exp(x^2 - y), [x, y], 4)
![]()
Мы запрашиваем дополнительные условия высшего порядка:
mtaylor(exp(x^2 - y), [x, y], 5)
![]()
В примере выше, ведущий термин имеет общую степень 0. В следующем примере ведущий термин имеет общую степень 2. Таким образом режим по умолчанию RelativeOrder производит условия общей степени меньший than4 + 2 = 6:
mtaylor(x*y*exp(x^2 - y), [x, y], 4)
![]()
Мы запрашиваем абсолютный порядок усечения 4, так, чтобы только условия общей степени, меньшей, чем 4, были вычислены:
mtaylor(x*y*exp(x^2 - y), [x, y], AbsoluteOrder = 4)
![]()
Поскольку бесконечные расширения указывают, что ряд в обратной величине переменной возвращен:
mtaylor(exp(z)/(x - y), [x = infinity, y = 0, z])

Мы уменьшаем порядок в z путем предоставления z более высокого веса:
mtaylor(exp(z)/(x - y), [x = infinity, y = 0, z], [1, 1, 2])

Если расширение Ряда Тейлора не существует, или если mtaylor не может найти расширение Ряда Тейлора, то mtaylor выдает ошибку.
Попытайтесь найти расширение Ряда Тейлора![]() приблизительно x = 1, y = 1. Расширение Ряда Тейлора не существует, и
приблизительно x = 1, y = 1. Расширение Ряда Тейлора не существует, и mtaylor выдает ошибку:
mtaylor(1/(x*y - 1), [x = 1, y = 1])
Error: Unable to compute Taylor expansion of '1/(x*y - 1)'. [mtaylor]
Это - пример направленного Разложения Тейлора вдоль вещественной оси вокруг x = infinity:
mtaylor(sqrt(y)*sin(sqrt(y)/x), [x = infinity, y = 0])

На самом деле это - даже неориентированное расширение:
mtaylor(sqrt(y)*sin(sqrt(y)/x), [x = complexInfinity, y = 0])
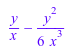
Типичной проблемой в символьных вычислениях является “выпуклость выражения”: промежуточные выражения, которые не являются или не могут быть упрощены вывод до излишне сложных результатов. Следующее является примером такого поведения:
mtaylor((a+x)^n, x, 4)
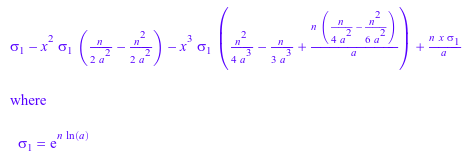
В целом применение simplify или Simplify к сложным результатам является стратегией, которая часто помогает. В этом случае, однако, это уничтожило бы формат ряда:
simplify(%)
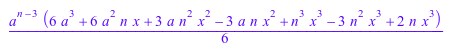
То, что требуется, является способом сопоставить функцию как simplify к коэффициентам ряда только. Поскольку mtaylor возвращает обычное выражение, это должно быть сделано в самом вызове mtaylor, с помощью опции Mapcoeffs:
mtaylor((a+x)^n, x, 4, Mapcoeffs=simplify)

|
Арифметическое выражение, представляющее функцию в |
| |
|
Точки расширения: арифметические выражения. Также выражения, включающие Если не заданный, точка 0 расширения по умолчанию используется. |
|
Порядок усечения (в сочетании с Концепция порядка относится к общей степени в области переменных (сумма всех экспонент). |
|
Один из флагов |
|
Список положительных целых чисел, определяющих количество условий вычисленного ряда. Переменная По умолчанию все переменные имеют вес 1. |
|
С этим флагом целочисленное значение |
|
С этим флагом условиями в вычисленном серийном диапазоне от некоторой ведущей общей степени |
|
Опция, заданная как Когда создание получившегося выражения, для каждого коэффициента |
Арифметическое выражение.
f
O | Series::Puiseux | Type::Series | asympt | diff | limit | series | taylor