Пример 1

Чтобы задать обыкновенное дифференциальное уравнение, используйте команду ode:

o:= ode(y'(x) = y(x)^2, y(x))

Решить уравнение, введите:

ode::solve(o)

или более эффективно:

solve(o)

Внутренне, функциональный ode::solve вызывает функциональный solve.

Пример 2

Можно решить обыкновенное дифференциальное уравнение с символьным параметром и начальным условием:

o:= ode({y'(x) = a*y(x)^2, y(a) = ln(a)}, y(x)):
solve(o)

Чтобы сократить количество возвращенных решений, используйте опцию IgnoreSpecialCases. Например, можно пропустить решение для параметра a = 1:

solve(o, IgnoreSpecialCases)

С опцией IgnoreSpecialCases возвращенный набор решений может быть неполным.

Пример 3

Решатель может возвратить решения piecewise:

o:= ode(y'(x) = a/y(x)^2 + b*y(x), y(x)):
solve(o)

Это решение завершено, и математически исправьте для всех возможных значений параметра a и переменную x. Также можно попробовать опцию IgnoreAnalyticConstraints, чтобы получить конкретное решение, которое правильно под набором общих предположений:

solve(o, IgnoreAnalyticConstraints)

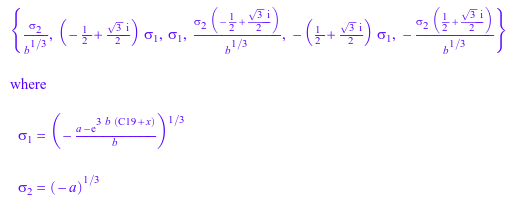
Решатель принимает несколько опций:

solve(o, Type = Bernoulli, IgnoreAnalyticConstraints)

Пример 4

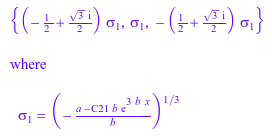
Предположим, вы хотите решить обыкновенное дифференциальное уравнение от класса Бернуллиевых уравнений:

o:= ode(y'(x) = (- 1/x + 2*I)*y(x) + 1/x*y(x)^2, y(x)):
solve(o)

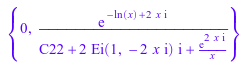
Решатель распознает тип уравнения и использует алгоритм для решения Бернуллиевых уравнений. Чтобы улучшать производительность, можно явным образом передать тип уравнения к решателю:

solve(o, Type = Bernoulli)

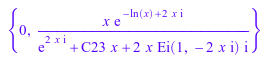
Решить уравнение Клеро с начальными условиями, введите:

o:= ode({(x*y'(x)-y(x))^2 - y'(x)^2 - 1 = 0, y(1) = 1}, y(x)):
solve(o, Type = Clairaut)

Если решатель не может идентифицировать уравнение с типом, вы указали, это выдает предупреждение и возвращает специальное значение FAIL:

o:= ode({(x*y'(x)-y(x))^2 - y'(x)^2 - 1 = 0, y(1) = 1}, y(x)):
solve(o, Type = Lagrange)

Warning: Unable to detect Lagrange ODE. [ode::lagrange]

Пример 5

Некоторые обыкновенные дифференциальные уравнения принадлежат нескольким классам. Например, некоторые уравнения Chini являются также гомогенными, и некоторые Лагранжевы уравнения являются также уравнениями Клеро. Если уравнение принадлежит нескольким классам одновременно, решатель может представить свое решение в различных формах. Форма решения зависит от класса, с которым идентифицировано уравнение. Например, предположите, что вы хотите решить дифференциальное уравнение Chini. Можно явным образом передать тип уравнения к решателю:

o:= ode(y'(x) = 1/x*y(x)^2 + 1/x*y(x) + x, y(x)):
L:= solve(o, Type = Chini)

Также можно позволить решателю распознать тип уравнения:

solve(o)

Решатель не возвращает тип, с которым внутренне идентифицировано обыкновенное дифференциальное уравнение. Если вы хотите проверить, что оба набора решения эквивалентны, используйте функцию rewrite с целевым exp на первом наборе решений:

rewrite(L, exp)

Пример 6

MuPAD^® решает некоторые классы обыкновенных дифференциальных уравнений Riccati, которые включают произвольные функции. Например, следующее уравнение содержит произвольный функциональный f(x):

eq := diff(y(x), x) - f(x)*y(x)^2 + a^2*x^(2*n)*f(x) - a*n*x^(n - 1)

Для этого уравнения возвращается решатель:

solve(ode(eq,y(x)))

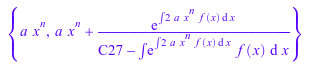
Также можно решить уравнение больше чем с одной произвольной функцией. Например, следующие уравнения содержат f(x) и g(x):

eq:= diff(y(x), x) - g(x)*f(x)*y(x) - g(x) - diff(f(x), x)*y(x)^2

Возвращенное решение:

solve(ode(eq,y(x)))

Пример 7

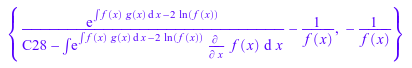
Предположим, вы хотите решить следующее обыкновенное дифференциальное уравнение второго порядка:

eq := x^2*(x^2 + 1)*diff(y(x),x,x) +
      x*(2*x^2 + 1)*diff(y(x),x) -
     (nu*(nu + 1)*x^2 + n^2)*y(x)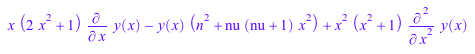

Решатель возвращает результат с точки зрения гипергеометрической функции ₁F₂ (см. hypergeom):

solve(ode(eq,y(x)))

Пример 8

Решатель может обработать некоторую треть - и обыкновенные дифференциальные уравнения высшего порядка. Например, решите следующие линейные дифференциальные уравнения третьего порядка:

eq := ode(sin(x)*y'''(x) + cos(x)*y(x), y(x)):
solve(eq)

eq := ode(6*y(x) + x^3*y'''(x), y(x)):
solve(eq)

Пример 9

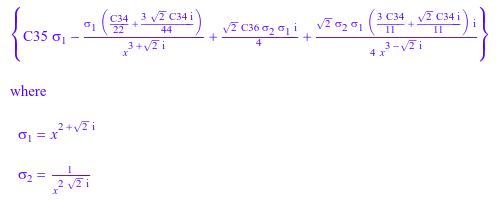
Решатель также может обработать некоторые нелинейные обыкновенные дифференциальные уравнения первого порядка. Например, решите следующие линейные дифференциальные уравнения первого порядка:

eq := ode(y(x)*diff(y(x), x) - y(x) - x^3 - 4*x^4 - 4*x^7, y(x)):
solve(eq)

eq := ode(exp(x/2)/4 - 2*exp(x) - y(x) + x*exp(x/2) + y(x)*y'(x), y(x)):
solve(eq)

Возвращаемые значения

Набор решений обыкновенного дифференциального уравнения или специального значения FAIL. Для получения дополнительной информации о возвращаемых значениях смотрите страницу справки solve.

Ссылки

Для получения дополнительной информации о конкретных классах обыкновенных дифференциальных уравнений см.: