статистика::Фильтр Ходрик-Прескотта
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::hodrickPrescottFilter([x1, x2, …],p) stats::hodrickPrescottFilter(s, <c>,p)
stats::hodrickPrescottFilter([x1, x2, …], p) возвращает список данных, из которых циклических изменений временных рядов, данных входными данными x 1, x 2 и т.д. устраняется с помощью процесса фильтра Ходрик-Прескотта.
Схема фильтра Ходрик-Прескотта пытается разделить временные ряды, состоящие из данных x 1, x 2 и т.д. в “тренд”, который приблизительно линеен вовремя плюс “циклический” вклад. Данные, возвращенные stats::hodrickPrescottFilter, описывают тренд. Циклическая часть c может быть вычислена
x := [x1, x2, ...]:
y := stats::HodrickPrescottFilter(x, p):
c := zip(x, y, _subtract):
Таким образом, x i = y i + c i.
Большие значения параметра штрафа p ведут, чтобы сглаживать прямые кривые тренда. Cf. Пример 5.
Если данные обеспечиваются объектом stats::sample, содержащим только один столбец нестроки, индекс столбца, c является дополнительным. Cf. Пример 3.
Внешние статистические данные, сохраненные в ASCII-файле, могут быть импортированы в сеанс MuPAD® через import::readdata. В частности, смотрите Пример 1 из соответствующей страницы справки.
Мы применяем фильтр Ходрик-Прескотта к некоторым данным. Результат показывает очевидный тренд к увеличению значений данных:
stats::hodrickPrescottFilter([1, 2, 3, 2, 3, 4, 3, 4, 5], 10)
![]()
Мы создаем выборку:
s := stats::sample([[i + frandom() - 0.5, -i + frandom() - 0.5]
$ i = 1..10])0.7703581656 -0.6689628213 1.653156516 -1.505187219 2.766272902 -3.319835772 3.952083055 -3.821218044 4.854984926 -4.818141187 6.221918655 -6.026170226 7.288981492 -7.288474164 8.355687175 -8.455102606 9.379160127 -8.580615152 10.23505742 -9.712454973
Процесс фильтра Ходрик-Прескотта применился к данным в первых урожаях столбца:
p := 10: stats::hodrickPrescottFilter(s, 1, p)
![]()
stats::hodrickPrescottFilter(s, 2, p)
![]()
delete s, p:
Мы создаем выборку, состоящую из одного столбца строки и одного столбца нестроки:
s := stats::sample([["1996", 1242],
["1997", 1353],
["1998", 1142],
["1999", 1255],
["2000", 1417],
["2001", 1312],
["2002", 1440],
["2003", 1422],
["2004", 1470]
])"1996" 1242 "1997" 1353 "1998" 1142 "1999" 1255 "2000" 1417 "2001" 1312 "2002" 1440 "2003" 1422 "2004" 1470
Мы применяем фильтр Ходрик-Прескотта к второму столбцу. В этом случае этот столбец не должен быть задан, поскольку это - единственный столбец нестроки:
y := stats::hodrickPrescottFilter(s, 10)
![]()
Мы преобразовываем этот список в демонстрационный объект:
y := stats::sample(y)
1239.848378 1255.015604 1270.397993 1296.009146 1329.022865 1362.512038 1398.347268 1433.347951 1468.498758
Мы создаем новую выборку, состоящую из отфильтрованных данных:
stats::concatCol(stats::col(s, 1), y)
"1996" 1239.848378 "1997" 1255.015604 "1998" 1270.397993 "1999" 1296.009146 "2000" 1329.022865 "2001" 1362.512038 "2002" 1398.347268 "2003" 1433.347951 "2004" 1468.498758
delete s, y:
Мы моделируем ежемесячные данные с затухающим трендом![]() , где i является индексом месяца. Эти данные о тренде затенены циклическими вкладами и случайным шумом:
, где i является индексом месяца. Эти данные о тренде затенены циклическими вкладами и случайным шумом:
monthlyData:= i ->
( 1/(1 + 0.01*i) // the trend
+ 0.7*cos(i * 1.12*2*float(PI)) // cycle
+ 0.3*sin(i * 2.04*4*float(PI)) // cycle
+ 0.2*cos(i * 1.01*6*float(PI)) // cycle
+ 2.3*frandom() // random noise
):Мы обеспечиваем ежемесячные данные в течение 10 лет, т.е. 120 месяцев. Циклические вклады и шум устраняются из временных рядов процессом фильтра Ходрик-Прескотта:
n := 120: x := [monthlyData(i) $ i = 1..n]: trend := stats::hodrickPrescottFilter(x, 10^5): cycle := zip(x, trend, _subtract):
Мы визуализируем разделение временных рядов (черных) приблизительно в линейный вклад тренда (красный) плюс циклическая (синяя) часть:
plot( plot::Listplot([[i, x[i]] $ i = 1..n], Color = RGB::Black), plot::Listplot([[i, trend[i]] $ i = 1..n], Color = RGB::Red), plot::Listplot([[i, cycle[i]] $ i = 1..n], Color = RGB::Blue) )

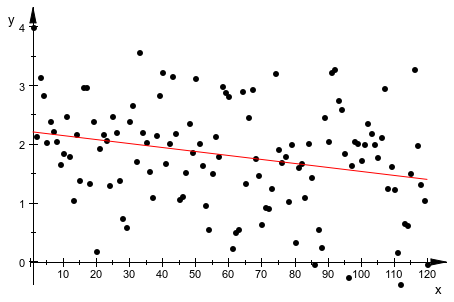
Мы используем scatterplot, чтобы визуализировать линейную регрессию неотфильтрованных данных. Линия регрессии находится в хорошем соответствии с линией тренда выше:
plot(plot::Scatterplot([[i, x[i]] $ i = 1..n]))
delete monthlyData, n, x, trend, cycle:
Мы демонстрируем эффект параметра штрафа p анимированным графиком:
delete p:
n := 100:
data := [1/(1 + 0.01*i) + frandom() $ i = 1..n]:
for i from 0 to 30 step 1/5 do
trend := stats::hodrickPrescottFilter(data, 10^(0.2*i));
L[i] := plot::Listplot([[i, trend[i]] $ i = 1..n],
Color = RGB::Red, VisibleFromTo = i .. i + 0.2);
T[i] := plot::Text2d(expr2text(p = 10^(0.2*i)), [70, 1.7],
VisibleFromTo = i .. i + 0.2);
end_for:
plot(plot::Listplot([[i, data[i]] $ i= 1..n], Color=RGB::Black),
L[i] $ i = 0..30 step 1/5, T[i] $ i = 0..30 step 1/5)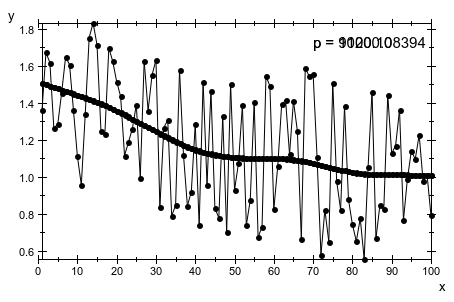
Большой результат p параметров штрафа в кривых тренда, которые являются близко к прямой линии. Это - не всегда желаемая информация. Следующая анимация показывает временные ряды с параболической кривой тренда, затененной случайным шумом. Слишком большие значения p производят кривую тренда, которая только отображает среднее значение данных:
data := [8*frandom() + 5 - (i - 50)^2/100 $ i = 1..n]:
for i from 0 to 50 do
trend := stats::hodrickPrescottFilter(data, 10^(0.2*i));
L[i] := plot::Listplot([[i, trend[i]] $ i = 1..n],
Color = RGB::Red,
VisibleFromTo = i/5 .. (i + 1)/5);
T[i] := plot::Text2d(expr2text(p = 10^(0.2*i)), [50, -5],
VisibleFromTo = i/5 .. (i + 1)/5);
end_for:
plot(plot::Listplot([[i, data[i]] $ i= 1..n], Color=RGB::Black),
L[i] $ i = 0..50, T[i] $ i = 0..50)
delete n, data, i, trend, L, T:
|
Статистические данные (временные ряды): арифметические выражения. |
|
Выборка доменного типа |
|
Целое число, представляющее индекс столбца демонстрационного s. Этот столбец предоставляет данным x 1, x 2 и т.д. |
|
Параметр штрафа схемы Ходрик-Прескотта: действительное положительное численное значение. Если данные, x 1, x 2 и т.д. представляет ежемесячные измерения, литература, рекомендуют значения p между 100 0 и 140 0. Если данные представляют ежеквартальные измерения, значения p, приблизительно 1 600 рекомендуются. Если данные представляют ежегодные измерения, значения p между 6 и 14 рекомендуются. |
Список данных с плавающей точкой.
Роберт Ходрик и Эдвад К. Прескотт, “послевоенные американские деловые циклы: эмпирическое расследование”. Журнал денег, кредита и банковского дела, 1997.
Maravall, Агустин и Ана Дель-Рио, “Агрегация времени и Фильтр Ходрик-Прескотта”, Банко де Эспана, 2001.