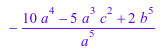Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Предположим, что у вас есть выражение с набором дискретных значений переменной. Вычисление суммы этого выражения по набору переменных называется суммированием. Переменная, по которой вы вычисляете сумму, называется индексом суммирования. Функция, которую вы получаете в результате символьного суммирования, вызвана антиразличие. MuPAD® неявно принимает, что индекс суммирования использует только целочисленные значения. Для непрерывных значений переменной суммирование естественно обращается к интегрированию. Так же к интегрированию, можно вычислить неопределенные и определенные суммы включая суммы по корням полиномов.
Функция![]() вызвана неопределенная сумма x i по
вызвана неопределенная сумма x i по i, если следующая идентичность содержит для всех значений i:
![]() .
.
Когда вы вычисляете неопределенную сумму, результат часто включает намного более сложные функции, чем те, вы используете в исходном выражении. Если исходное выражение состоит из элементарных функций, можно получить результат с точки зрения элементарных функций:
sum(x^2/(x^2 - 1), x)
![]()
Несмотря на то, что следующее выражение состоит из элементарных функций, результат включает специальную функцию:
sum(x/(x^2 + 1), x)
![]()
При вычислении неопределенной суммы команда sum неявно принимает, что индекс интегрирования пробегает все целые числа. Определенное суммирование позволяет вам задать область значений индекса суммирования. Например, задайте индексную область значений суммирования с помощью символьного параметра:
sum(x/(x^2 + 1), x = a..10*a)
![]()
sum также вычисляет определенные суммы с бесконечными контурами:
sum(x^n/n!, n = 0..infinity); sum((-1)^n*x^(2*n + 1)/(2*n + 1)!, n = 0..infinity)
![]()
![]()
Чтобы найти сумму более чем двумя переменными, используйте вложенные вызовы sum:
sum(sum(x^n/n!, n = 0..infinity), x = a..100*a)
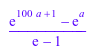
Если ваша сумма имеет небольшое конечное число условий, используйте команду _plus вместо sum. Команда sum медленнее, чем _plus:
_plus(x/(x^2 + 1) $ x = 0..10)
![]()
Чтобы вычислить сумму для большого конечного числа условий, используйте команду sum:
sum(x/(x^2 + 1), x = 1..10^10)
![]()
Если результат конечного суммирования содержит больше чем 1 000 условий, команда sum возвращает нерасширенную символьную сумму. Если вы хотите отобразить все условия явным образом, используйте функцию expand. Чтобы получить расширенный результат в следующем примере, удалите двоеточие в конце примера:
S := sum(exp(x)/(x^2 + 1), x = a..a + 1000); expand(S):
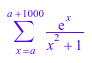
Команда sum также вычисляет суммы, за которые индекс суммирования работает на основе всех корней полинома. Чтобы задать все корни полинома, используйте RootOf:
sum(i^10, i = RootOf(a*X^10 + b*X^8 + c*X^5 + 1, X))