EiИнтегральная показательная функция
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Ei(x) Ei(n, x)
Ei(x) представляет экспоненциальный интеграл![]() .
.
Ei(n, x) представляет экспоненциальный интеграл![]() .
.
Если x число с плавающей запятой, затем Ei(x) возвращает численное значение экспоненциального интеграла. Специальные значения Ei (∞) = ∞ и Ei (-∞) = 0 реализованы. Для всех других аргументов, Ei(x) возвращает символьный вызов функции.
Если оба n и x численные значения и если по крайней мере один из них является числом с плавающей запятой, то Ei(n, x) возвращает значение с плавающей точкой.
Специальные значения Ei (n, ∞) = 0 и Ei (n, - ∞) = - ∞ реализованы для произвольного n.
Если n неположительное целое число, не больше, чем Pref::autoExpansionLimit(), затем Ei(n, x) возвращает явное выражение формы exp(-x)*p(1/x), где p полином степени 1 - n. Например:
![]() .
.
Используйте expand если такие представления также желаемы для |n| больше, чем Pref::autoExpansionLimit().
Если x положительная константа, Ei(1, x) возвращает - Ei(-x). Для отрицательного постоянного x, Ei(1, x) возвращает - Ei(-x) - π i.
Для всех других аргументов Ei(n, x) возвращает символьный вызов функции.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
Мы демонстрируем некоторые вызовы с точными и символьными входными данными:
Ei(1), Ei(sqrt(2)), Ei(x + 1), Ei(infinity), Ei(-infinity)
![]()
Ei(sqrt(2), PI), Ei(2, x + 1), Ei(3, infinity), Ei(I, -infinity)
![]()
Если первый аргумент является неположительным целым числом, явное выражение возвращено:
Ei(-5, x)
![]()
Значения с плавающей точкой вычисляются для аргументов с плавающей точкой:
Ei(-1000.0), Ei(1.0), Ei(12.3), Ei(2.0 + 10.0*I)
![]()
Ei(3, -1000.0), Ei(1 + I, 1.0), Ei(-2, 12.3), Ei(1.0 + I, 2 + 10*I)

Для положительного постоянного x, Ei(1, x) возвращает - Ei(-x). Для отрицательного постоянного x, Ei(1, x) возвращает - Ei(-x) - π i:
Ei(1, 3), Ei(1, -3)
![]()
Функциональный Ei(x) с 1 аргументом сингулярно в начале координат:
Ei(0)
Error: Singularity. [Ei]
Отрицательная вещественная ось является разрезом. Скачок высоты 2 π i происходит при пересечении этого сокращения:
Ei(-1.0), Ei(-1.0 + 10^(-10)*I), Ei(-1.0 - 10^(-10)*I)
![]()
Системные функции, такие как diff, float, limitрасширение, и series обработайте выражения, включающие Ei:
diff(Ei(x), x, x, x), float(ln(3 + Ei(sqrt(PI))))
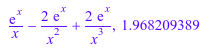
diff(Ei(3, x), x, x, x), float(ln(3 + Ei(I, sqrt(PI))))
![]()
limit(Ei(2*x^2/(1+x)), x = infinity)
![]()
expand(Ei(3, x))
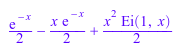
series(Ei(3, x), x = 0, 3)
![]()
series(Ei(7/2, x), x = infinity, 3)
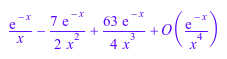
|
Арифметическое выражение.
nX
Если n неположительное целое число, затем Ei(n, x) аналитическая функция x в комплексной плоскости кроме полюса в начале координат. Для всех других значений n, функциональный Ei(n, x) имеет разрез вдоль отрицательной действительной полу оси, где значения совпадают с пределом “сверху”:
![]()
для действительного x <0.
Функциональный Ei(x) с 1 аргументом связан с функцией с 2 аргументами
![]() .
.
Это имеет логарифмическую сингулярность в начале координат и разрезе вдоль отрицательной вещественной оси. В отличие от функционального Ei(n, x) с 2 аргументами функциональный Ei с 1 аргументом (x) не непрерывен ни от одного выше или ниже вдоль разреза.
Функции Ei(n, x) связаны с неполной гамма функцией igamma ![]() .
.
Функции Ei(x) и Ei(n, x) соответствуйте интегральным показательным функциям Ei (x) и E n (x), рассмотренный в М. Абрамовице и мне. Stegun, “Руководство Математических функций”, Dover Publications Inc., Нью-Йорк (1965).