`linalg`::`sylvester`

Матрица Сильвестра двух полиномов

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

linalg::sylvester(p, q)
linalg::sylvester(f, g, x)

Описание

linalg::sylvester(p, q) возвращает матрицу Сильвестра этих двух полиномов p и q.

Если никакая переменная не задана, то полиномы p и q должен иметь любой доменный DOM_POLY или от области категории Cat::Polynomial. Многочленные выражения не позволены.

Если полиномы p и q имеют доменный DOM_POLY, затем они должны быть одномерными полиномами. Звонок компонента матрицы Сильвестра является общим содействующим звонком R p и q, кроме следующих двух случаев для встроенных содействующих звонков: Если R является Expr затем доменный Dom::ExpressionField() звонок компонента матрицы Сильвестра. Если R является IntMod(m), затем матрица Сильвестра задана по кольцевому Dom::IntegerMod(m) (см. Пример 2).

В противном случае, если полиномы p и q от области категории Cat::Polynomial, затем матрица Сильвестра вычисляется относительно основной переменной p и q (см. метод "mainvar" из категории Cat::Polynomial). В случае одномерных полиномов матрица Сильвестра задана по общему содействующему звонку p и q. В случае многомерных полиномов матрица Сильвестра задана по кольцевому Dom::DistributedPolynomial компонента(ind, R), где ind список всех переменных p и q кроме x, и R общий содействующий звонок полиномов.

Если f и g многочленные выражения или многомерные полиномы типа DOM_POLY, затем вы должны specifiy переменная x.

В случае многочленных выражений звонком компонента матрицы Сильвестра является доменный Dom::ExpressionField() (см. Пример 3).

В случае многомерных полиномов матрица Сильвестра задана по кольцевому Dom::DistributedPolynomial(ind, R) компонента, где ind список всех переменных f и g кроме x, и R общий содействующий звонок полиномов (см. Пример 4).

По крайней мере один из входных полиномов должен иметь положительную степень относительно основной переменной или x, соответственно, но не необходимо, чтобы у них обоих была положительная степень.

Примеры

Пример 1

Матрица Сильвестра этих двух полиномов p = x ² + 2 x - 1 и q = x ⁴ + 1 по ℤ является следующим 6×6 матрица:

delete x: Z := Dom::Integer:
S := linalg::sylvester(poly(x^2 + 2*x - 1, Z), poly(x^4 + 1, Z))

Пример 2

Если полиномы имеют встроенный содействующий звонок IntMod(m), затем матрица Сильвестра задана по доменному Dom::IntegerMod(m):

delete x: 
S:= linalg::sylvester( 
  poly(x + 1, IntMod(7)), poly(x^2 - 2*x + 2, IntMod(7)) 
)

domtype(S)

Пример 3

Матрица Сильвестра следующих двух многочленных выражений относительно переменной x :

delete x, y: 
S := linalg::sylvester(x + y^2, 2*x^3 - 1, x)

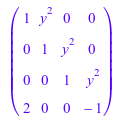
domtype(S)

Матрица Сильвестра этих двух полиномов относительно y следующий 2×2 матрица:

linalg::sylvester(x + y^2, 2*x^3 - 1, y)

Пример 4

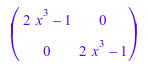
Вот пример для вычисления матрицы Сильвестра многомерных полиномов:

delete x, y: Q := Dom::Rational:
T := linalg::sylvester(poly(x^2 - x + y, Q), poly(x + 2, Q), x)

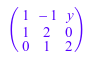
domtype( T )

Матрица Сильвестра этих двух многомерных полиномов относительно y :

linalg::sylvester(poly(x^2 - x + y, Q), poly(x + 2, Q), y)

Параметры

`pQ`	Многочлены
`fG`	Полиномы или многочленные выражения положительной степени
`x`	Переменная

Возвращаемые значения

Матрица доменного Dom::Matrix(R), где R содействующая область полиномов (см. ниже).

Документация