logЛогарифм к произвольной основе
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Для войдите в систему MATLAB®, смотрите log.
log(b,x) log(x)
Выход синтаксиса log(b, x) был изменен и переписан в терминах натуральных логарифмов как ln(x)/ln(b).
log(b, x) представляет логарифм x к основному b.
log(x) псевдоним для натурального логарифма ln(x).
Математически,
совпадает с ln(x)/ln(b). Когда вы вызываете log, результат переписан в терминах натуральных логарифмов.
Логарифм задан для всех сложных аргументов x ≠ 0. Основной b, однако, принят, чтобы быть действительным, положительным и не равным 1.
Для символьного b, MuPAD® применяет упрощения на основе этих предположений.
log применяет следующие правила упрощения к его аргументам:
в следующих случаях:
b символьный (индексируемый) идентификатор и x имеет тип Type::Real
b является числовым и x целое число или рациональный.
Математически, это правило допустимо для любого действительного значения x.
Если x отрицательное целое число или рациональное отрицание, затем
.
Если x является целым числом, то
.
log использует следующие специальные значения:
, 
, 
, 
.
Для точных числовых и символьных аргументов, log переписывает вызов функции в терминах натурального логарифма.
Если оба аргумента являются числовыми, и по крайней мере один из них является числом с плавающей запятой, log возвращает результат с плавающей точкой. Мнимая часть результата принимает значения в интервале
если b> 1 и в интервале
если b <1. Отрицательная вещественная ось является разрезом, мнимой частью скачков результата при пересечении сокращения. На отрицательной вещественной оси мнимая часть
согласно
, x <0. Смотрите Пример 3.
Арифметические правила те, которые
не допустимы в комплексной плоскости. Используйте свойства отметить идентификаторы как действительные и применить функции, такие как expand или simplify управлять выражениями, включающими log. Смотрите пример 4.
Когда названо аргументом с плавающей точкой, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность.
При вычислении логарифма к произвольной основе используйте идентификаторы, индексированные идентификаторы или количества типа Type::Positive задавать основу логарифма:
log(b, 2), log(b[1], 3), log(2, 5), log(2/3, 4/9), log(0.3, x)
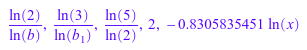
Не используйте общие арифметические выражения, чтобы задать основу:
log(-PI^2, 2)
Error: Base must be an identifier, an indexed identifier, or a positive real number. [log]
Для аргументов с плавающей точкой, log возвращает результаты с плавающей точкой:
log(2, 123.4), log(2.0, 5.6 + 7.8*I), log(10.0, 2/10^20)
log применяет специальные правила упрощения к его аргументам:
log(b, 1), log(b, -1), log(2/3, (4/9)^10), log(b, b^(-5))
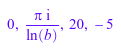
diff, float, limit, series и подобные функции обрабатывают выражения, включающие log:
diff(log(b, x^2), x)
float(log(10, PI + I))
limit(log(10, x)/x, x = infinity)
series(x*log(x, sin(x)), x = 0)
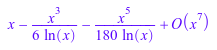
Отрицательная вещественная ось является разрезом. Мнимая часть значений возвращена log перейдите при пересечении этого сокращения:
log(10, -2.0), log(10, -2.0 + I/10^1000), log(10, -2.0 - I/10^1000)
expand и simplify реагируйте на набор свойств через assume. Следующий вызов не приводит к расширенному результату, потому что арифметическое правило
не содержит для произвольного комплексного x, y:
expand(log(10, x*y))
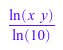
Если один из факторов действителен и положителен, правило допустимо:
assume(x > 0): expand(log(b, x*y))
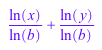
simplify(log(b, x^3*y) - log(b, x))
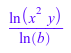
Для дальнейших расчетов очистите предположение:
unassume(x):
|
Идентификатор доменного типа |
|
Арифметическое выражение
x