OОбласть условий порядка (символы Ландау)
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
O(f, <x = x0, y = y0, …>)
O(f, x = x0) представляет символ Ландау![]() .
.
Математически, для функционального f в переменных (x, y, …), символ Ландау
![]()
функция в этих переменных со следующим свойством: там существует постоянный c и окружение предельной точки (x 0, y 0, …) таким образом что |g | ≤ c | f | для всех значений (x, y, …) в том окружении.
Как правило, символы Ландау используются, чтобы обозначить, что порядок называет (“остаточные члены”) последовательных расширений. Обратите внимание, однако, что последовательные расширения, произведенные asympt, series, и taylor представляйте условия порядка с должности части структур данных Series::Puiseux и Series::gseries; они не используют доменный O.
Уравнениями x = x0, y = y0 и т.д., f рассматривается как функция заданных переменных. Все другие идентификаторы содержатся в f рассматриваются как постоянные параметры.
Если никакие переменные и предельные точки не заданы, то все идентификаторы в f используются в качестве переменных, каждый стремящийся к предельной точке по умолчанию 0.
Переменные, стремящиеся к 0, не распечатаны на экране.
Переменные термина порядка могут быть получены с функциональным indets. Предельные точки могут быть запрошены с функциональным O::points.
Арифметические операции +, -, *, /, и ^ перегружаются для условий порядка.
Автоматические упрощения в настоящее время ограничиваются многочленными выражениями f. Одномерные многочленные выражения уменьшаются до ведущего одночлена расширения вокруг предельной точки. В многомерных многочленных выражениях все условия отбрасываются, которые делимые по условиям более низкоуровневым. Для немногочленных выражений только удалены целочисленные коэффициенты.
Для многочленных выражений происходят определенные упрощения:
O(x^4 + 2*x^2), O(7*x^3), O(x, x = 1)
![]()
Нулевая предельная точка не распечатана на экране:
O(1), O(1, x = 1), O(x^2/(y + 1), x = 0, y = -1, z = PI)
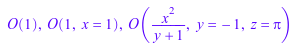
Арифметические операции перегружаются для условий порядка:
7*O(x), O(x^2) + O(x^13), O(x^3) - O(x^3), O(x^2)^2 + O(x^4)
![]()
Для многомерного многочленного выражения отбрасываются условия высшего порядка, если они делимые по условиям более низкоуровневым:
O(15*x*y^2 + 3*x^2*y + x^2*y^2)
![]()
O(x + x^2*y) = O(x)*O(1 + x*y)
![]()
Мы демонстрируем, как получить доступ к переменным и предельным точкам термина порядка:
a := O(x^2*y^2)
![]()
indets(a) = O::indets(a), O::points(a)
![]()
delete a:
|
Арифметическое выражение, представляющее функцию в |
|
Переменные: идентификаторы |
|
Предельные точки: арифметические выражения |
Элемент доменного O.