asymptВычислите расширение асимптотического ряда
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
asympt(f,x) asympt(f,x, <order>, <dir>) asympt(f,x = x0, <order>, <Left | Right>)
asympt(f, x) вычисляет первые сроки расширения асимптотического ряда f относительно переменной x вокруг точки infinity.
asympt используется для расчета асимптотическое расширение f когда x стремится к x0. Если такое расширение может быть вычислено, серийный объект доменного типа Series::gseries или Series::Puiseux возвращен.
В отличие от поведения по умолчанию series, asympt вычисляет направленные расширения, которые могут быть допустимыми вдоль действительной линии только.
asympt может вычислить более общие типы асимптотических расширений, чем связанный функциональный series. См. пример 5.
Если x0 регулярная точка f, полюс или алгебраическая точка разветвления, затем asympt возвращает расширение Пюизе. В этом случае рекомендуется использовать более быстрый функциональный series вместо этого.
Если asympt не может вычислить асимптотическое расширение, затем символьное выражение типа "asympt" возвращен. См. Пример 4.
Количеством требуемых условий для расширения является order если задано. В противном случае, значение переменной окружения ORDER используется. Можно изменить значение по умолчанию 6 путем присвоения нового значения ORDER.
Количество условий считается от самого низкого термина степени на для конечных точек расширения, и от самого высокого термина степени на для расширений вокруг бесконечности, т.е. “order” должен рассматриваться как “относительный порядок усечения”.
Фактическое количество условий в получившемся последовательном расширении может отличаться от требуемого количества условий. Смотрите series для деталей.
Функциональный asympt возвращает объект доменного типа Series::gseries или Series::Puiseux. Этим можно управлять через стандартные арифметические операции и различные системные функции. Например, coeff возвращает коэффициенты; expr преобразует ряд в выражение, удаляя остаточный член; lmonomial возвращает ведущий одночлен; lterm возвращает ведущий термин; lcoeff возвращает ведущий коэффициент; map применяет функцию к коэффициентам; nthcoeff возвращает n-th коэффициент, nthterm n-th термин и nthmonomial n-th одночлен.
Функция чувствительна к переменной окружения ORDER, который определяет количество по умолчанию условий в последовательных расчетах.
Мы вычисляем асимптотическое расширение для![]() :
:
s := asympt(sin(1/x + exp(-x)) - sin(1/x), x)
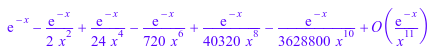
Ведущий термин и третий срок извлечены:
lmonomial(s), nthterm(s, 3)
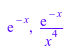
В следующем вызове требуют только 2 условия расширения:
asympt( exp(sin(1/x + exp(-exp(x)))) - exp(sin(1/x)), x, 2 )
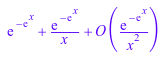
delete s:
Мы вычисляем расширение вокруг конечного основного назначения. По умолчанию расширение допустимо “направо” точки расширения:
asympt(abs(x/(1+x)), x = 0)
![]()
Различное расширение допустимо “налево” точки расширения:
asympt(abs(x)/(1 + x), x = 0, Left)
![]()
Следующее расширение точно. Поэтому это не имеет никакого “остаточного члена”:
asympt(exp(x), x = infinity)
![]()
Вот пример где asympt не может вычислить расширение асимптотического ряда:
asympt(cos(gamma(x*s))/s, x = infinity)
![]()
Если мы применяем функциональный series к следующему выражению это по существу возвращает само выражение:
series(sin(x)/x,x = 0)
![]()
В этом примере, asympt вычисляет более подробное последовательное расширение:
asympt(sin(x)/x, x = 0)
![]()
|
Арифметическое выражение, представляющее функцию в |
| |
|
Точка расширения: арифметическое выражение; если не заданный, точка расширения по умолчанию |
|
Количество условий, которые будут вычислены: неотрицательное целое число; распоряжение по умолчанию дано переменной окружения |
|
С |
Объект доменного типа Series::gseries или Series::Puiseux, или выражение типа "asympt".
f
O | ORDER | Series::Puiseux | Series::gseries | Type::Series | limit | mtaylor | series | taylor