plot::Streamlines2dПотоки векторных полей
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Streamlines2d([v1, v2],x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::Streamlines2d(v1,v2,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::Streamlines2d(V,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options)
plot::Streamlines2d( [v1, v2] , x = `x_{min}`..`x_{max}` , y = `y_{min}`..`y_{max}` ) создает потоки векторного поля, заданного![]() с (x, y) ∈ [x min, x max] × [y min, y max].
с (x, y) ∈ [x min, x max] × [y min, y max].
Векторное поле задано функцией![]() .
. plot::Streamlines2d отображает векторное поле путем рисования почти равномерно распределенных потоков векторного поля, т.е. изгибается, к которому векторное поле является тангенциальным в каждой точке. Плотностью линий потоков (и время, необходимое для вычисления), управляют с атрибутом MinimumDistance.
Как показывает опыт: уменьшение значения MinimumDistance фактором 2 приводит к увеличению времени выполнения фактором 4.
Схема определяемого пользователем цвета может быть задана LineColorFunction = color, где color процедура MuPAD®, принимающая 6 входных параметров и возвращающая список RGB значения. Во время графического вывода эта функция вызвана в форме color(x, y, v1, v2, t, l, n):
Значения xY координаты текущей точки.
Значения v1, v2 компоненты векторного поля в текущей точке.
Значение t “время” текущей точки (x, y) на текущем потоке. Масштабирование этого параметра зависит от векторного поля.
Значение l длина кривой текущего потока от его начальной точки текущая точка (x, y), как Евклидово расстояние. Этот параметр является инвариантным относительно скалярных изменений векторного поля (до изменения направления потока).
Целочисленное значение n количество текущего потока. Каждый отдельный поток имеет различное значение.
См. пример 3.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AbsoluteError | максимальная абсолютная ошибка дискретизации | |
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Black |
LineWidth | ширина линий | 0.35*unit::mm |
LineColor2 | цвет линий | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
MinimumDistance | пробел между линиями потоков | |
Name | имя объекта графика (для браузера и легенды) | |
ODEMethod | числовая схема, используемая в том, что решила ОДУ | ABM4 |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
RelativeError | максимальная относительная ошибка дискретизации | 1/100000 |
Stepsize | установите постоянный размер шага | |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
TipAngle | вводный угол наконечников стрелки | (2*PI)/15 |
TipStyle | стиль презентации наконечников стрелки | Filled |
TipLength | длина наконечников стрелки | 0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XFunction | функция для x значений | |
XMax | окончательное значение параметра “x” | |
XMin | начальное значение параметра “x” | |
XName | имя параметра “x” | |
XRange | область значений параметра “x” | |
YFunction | функция для y значений | |
YMax | окончательное значение параметра “y” | |
YMin | начальное значение параметра “y” | |
YName | имя параметра “y” | |
YRange | область значений параметра “y” |
plot::Streamlines2d изображает векторные поля (более или менее) равноотстоящими линиями потоков:
plot(plot::Streamlines2d(-x, -y, x=-2..2, y=-2..2))
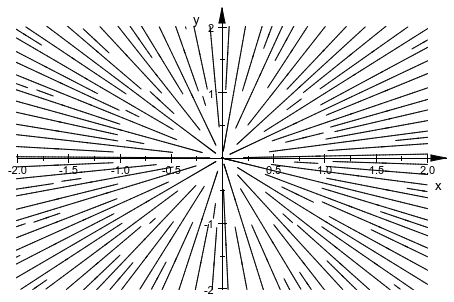
Обратите внимание на то, что этот стиль отображения обязательно повреждает симметрии, в этом случае совершенная осевая симметрия векторного поля.
Кроме того, циклы не будут закрыты, но оставят разрыв:
plot(plot::Streamlines2d(-y, x, x=-2..2, y=-2..2))
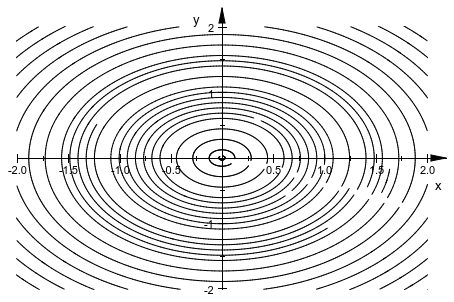
Кроме “обычных” параметров, таких как параметр располагается, цвет линии, или ширина линии, plot::Streamlines2d может управляться с атрибутом MinimumDistance, который устанавливает минимальное расстояние между линиями потоков:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2))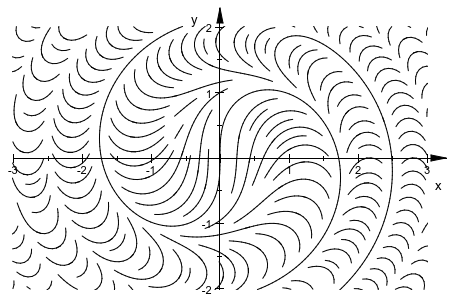
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
MinimumDistance = 0.2))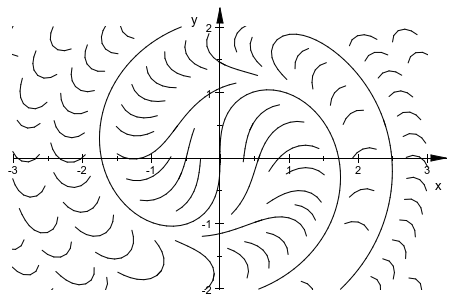
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
MinimumDistance = 0.05))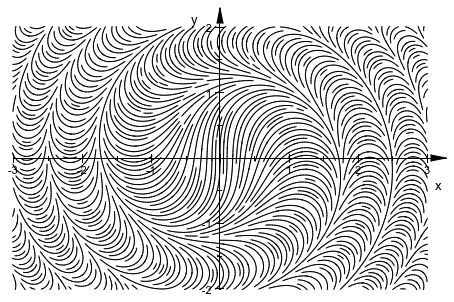
Функция цвета линии для plot::Streamlines2d имеет доступ к текущим координатам, к компонентам векторного поля в текущей точке, к текущей длине на кривой (и в терминах параметра “времени” и в терминах Евклидова расстояния) и целочисленное количество текущей кривой (которые не найдены в некотором предопределенном порядке). Мы используем номер кривой, чтобы сгенерировать красочное отображение:
num2col := (x, y, vx, vy, t, l, n) -> RGB::fromHSV([111*n, 1, 1]):
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
LineColorFunction = num2col))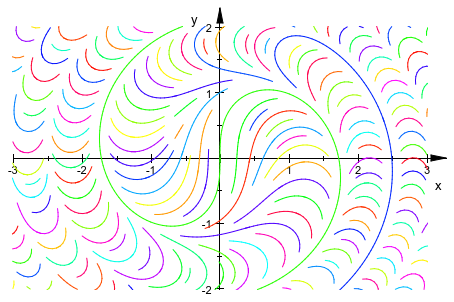
Используя кривую информация о длине позволяет нам включать направленную информацию в отображение:
l2col := (x, y, vx, vy, t, l) -> [frac(5*l) $ 3]:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2+y^2),
x = -3..3, y = -2..2,
LineWidth = 0.75,
LineColorFunction = l2col))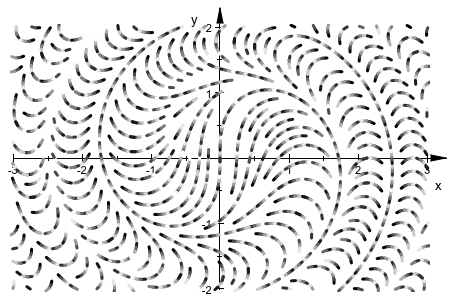
Часто, более легкий способ построить ориентацию линий потоков состоит в том, чтобы активировать наконечники стрелки plot::Streamlines2d графики в середину каждого достаточно долго) линия потоков. Они сделаны невидимыми длиной совета по умолчанию 0:
plot(plot::Streamlines2d(0.3*x-y, 0.3*y+x,
x = -3..3, y = -2..2,
TipLength = 3*unit::mm))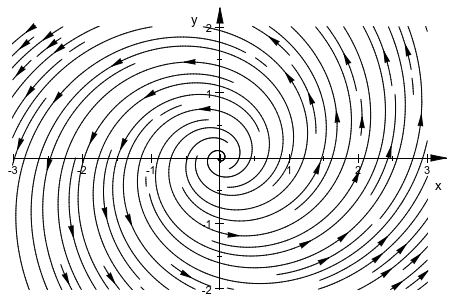
Поскольку размещение линий потоков трудно предсказать, plot::Streamlines2d не действительно подходит для анимаций. Возможно анимировать plot::Streamlines2d, но когерентность между кадрами анимации меньше чем обычно:
plot(plot::Streamlines2d(sin(x^2+y^2), cos(x^2-y^2+a),
x = -2..2, y = -2..2, a = -PI..PI,
MinimumDistance = 0.1,
Frames=10))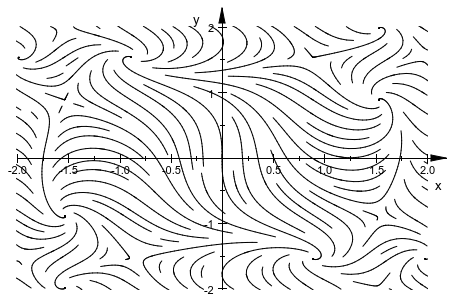
С настройками по умолчанию, plot::Streamlines2d не может построить векторное поле![]() (который не является непрерывным Липшицом) удовлетворяющим способом:
(который не является непрерывным Липшицом) удовлетворяющим способом:
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2))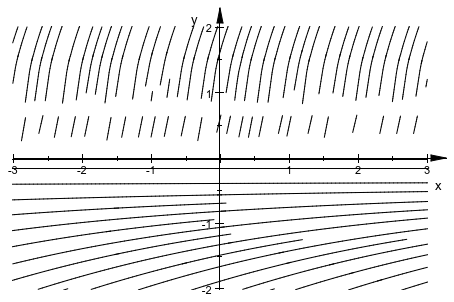
При помощи различного числового интегратора проблемы могут быть преодолены (за счет более длительного расчета):
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2,
ODEMethod=RKF43,
RelativeError=1e-3))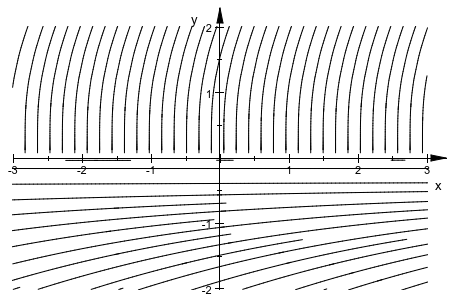
|
x - и y - компонент векторного поля: арифметические выражения в |
|
Матрица A категории |
|
Идентификаторы. |
|
Действительные численные значения.
|
|
Параметр анимации, заданный как |
Алгоритм используется в plot::Streamlines2d был опубликован в “Создании Равномерно распределенных Потоков Произвольной Плотности” Бруно Джобардом и Уилфридом Лефером на Еврографическом Семинаре в Boulogne-sur-Mer, Франция.