Атрибуты

Пример 1

Мы рассматриваем логистическую карту для значения параметров 3, т.е. парабола f (x) = 3 x   (1 - x) для x ∈ [0, 1]. Мы выполняем итерации начальной точки x ₀ = 0.5:

f :=  plot::Function2d(3*x*(1 - x), x = 0..1, 
                       Color = RGB::Blue):
x0 := 0.5:

Мы строим итерацию (не задавая количество итераций), парабола f и диагональная линия g (x) = x:

g := plot::Function2d(x, x = 0..1, Color = RGB::Red):  
it := plot::Iteration(3*x*(1 - x), x0, x = 0..1):   
plot(f, g, it)

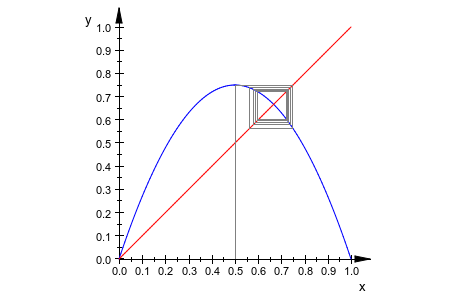
Мы увеличиваем число итераций к 50 и изменяем цвет линий к RGB::Black:

it::Iterations := 50:
it::Color := RGB::Black:
plot(f, g, it)

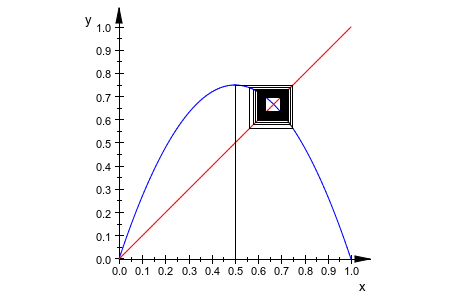
Наконец, мы анимируем количество шагов, позволяя проходить курс итерации:

it := plot::Iteration(3*x*(1 - x), x0, n, x = 0..1,
                      n = 1..50, Color = RGB::Black):
plot(f, g, it)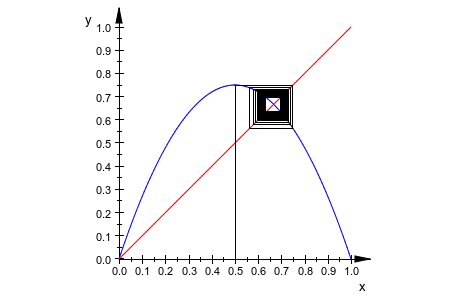

delete f, g, it:

Пример 2

Мы считаем логистическую карту f (x) = a  x   (1 - x) для x ∈ [0, 1] и параметр анимации a, запускающийся от a = 2 к a = 4:

f := plot::Function2d(a*x*(1 - x), x = 0..1, a = 2..4,
                      Color = RGB::Black):

Мы задаем итерацию начальной точки x ₀ = 0.2 f и строим его вместе с функциональным графиком f (x) и диагональная линия g (x) = x:

g := plot::Function2d(x, x = 0..1, Color = RGB::Black):
it1 := plot::Iteration(a*x*(1 - x), 0.2, 30, x = 0..1, 
                       a = 2..4, Color = RGB::Red):
plot(f, g, it1)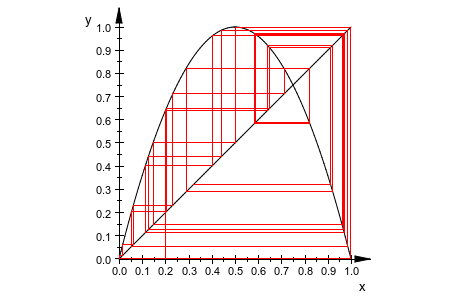

Мы задаем дополнительную итерацию, запускающуюся в x ₀ = 0.21, и добавляем его в график:

it2 := plot::Iteration(a*x*(1 - x), 0.21, 30, x = 0..1, 
                       a = 2..4, Color = RGB::Blue):
plot(f, g, it1, it2)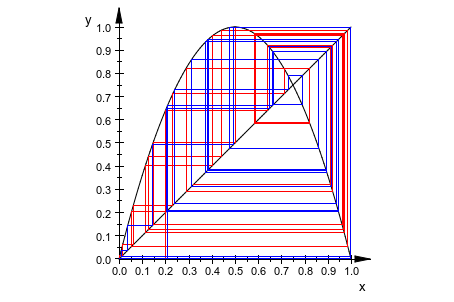

Для маленьких значений a эти две итерации сходятся к той же фиксированной точке. Когда a приближается к значению 4, дрейф итераций в хаос.

delete f, g, it1, it2:

Пример 3

Считайте итерацию начальной точки x ₀ = 0.2 логистической картой f (x) = x   (x - 1) с областью значений графика x ∈ [0, 1]:

f := plot::Function2d(x*(x - 1), x = 0..1):
it := plot::Iteration(x*(x - 1), 0.2, x = 0..1):
plot(f, it)

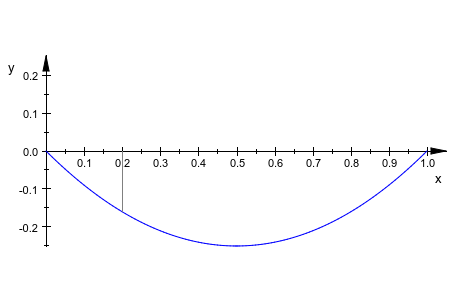
Мы видим, что только один шаг итерации построен. Причина состоит в том, что точка x ₁ = f (x ₀) отрицательна и, следовательно, не содержавшаяся в требуемой области значений графика x = 0..1. Мы modifiy область значений графика:

f::XRange:= -0.5..1:
it::XRange:= -0.5..1:
plot(f, it)

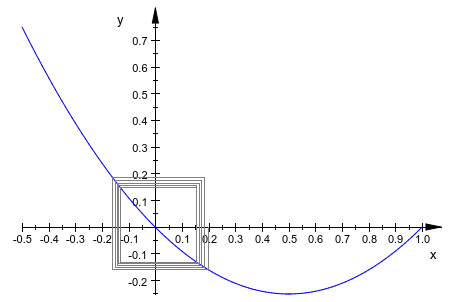
delete f, it:

Пример 4

Мы анимируем параметр n, который определяет номер итераций. Мы устанавливаем область значений времени для анимации к 40 (секунды). Используя Frames, общее количество систем координат выбрано таким образом, что приблизительно 10 систем координат используются, чтобы визуализировать шаг от n до n + 1:

f := plot::Function2d(4*x*(1 - x), x = 0..1):
g := plot::Function2d(x, x = 0..1):
it := plot::Iteration(4*x*(1 - x), 0.4, n, x = 0..1, 
                      LineStyle = Dashed,
                      n = 0..40, Frames = 411,
                      TimeRange = 0..40):
plot(f, g, it)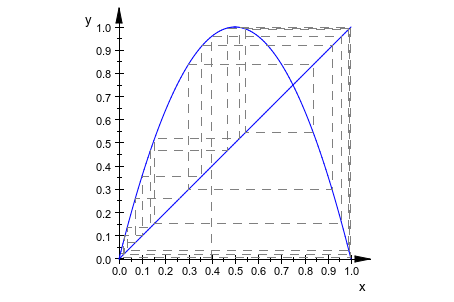

delete f, g, it: