plot::SphereГрафический примитив для сфер
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Sphere(r, <[cx, cy, cz]>, <a = amin .. amax>, options)
plot::Sphere(r, c) создает сферу радиуса r и центр c.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
Center | центр объектов, центр вращения | [0 |
CenterX | центр объектов, центр вращения, x-компонент | 0 |
CenterY | центр объектов, центр вращения, y-компонент | 0 |
CenterZ | центр объектов, центр вращения, z-компонент | 0 |
Color | основной цвет | RGB::LightBlue |
FillColor | цвет областей и поверхностей | RGB::LightBlue |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
Radius | радиус кругов, сферы и т.д. | 1 |
Shading | сглаживайте цветное смешение поверхностей | Smooth |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TitlePositionZ | положение объектных заголовков, z компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
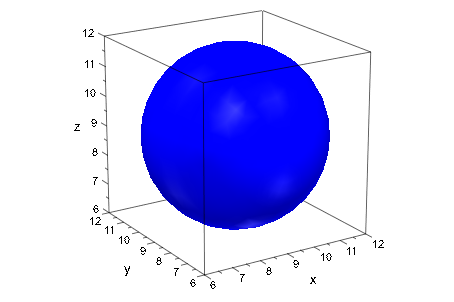
Создайте синюю сферу с центром (9, 9, 9) и радиус 3:
s := plot::Sphere(3, [9, 9, 9], Color = RGB::Blue)
![]()
Вызовите plot построить сферу:
plot(s)
delete s:
Создайте сферу с центром (-1, - 1, 5) и радиус 3. В двух точках на сфере добавьте 3D диски, указывающие на плоскости касательной.
c := [-1, -1, 3]: s := plot::Sphere(3, c): p1 := [ 1, -3, 4]: p2 := [-3, -2, 1]:
Диски создаются через plot::Circle3d как заполненные 3D круги радиуса 2.5, сосредоточенный в точках p 1 и p 2, соответственно. Нормали n i даны p i - c. Вычислите их subracting центр c от точек p i через zip:
n1 := zip(p1, c, _subtract):
n2 := zip(p2, c, _subtract):
t1 := plot::Circle3d(2.5, p1, n1, Filled = TRUE,
LineColor = RGB::Black,
FillColor = RGB::Red.[0.5]):
t2 := plot::Circle3d(2.5, p2, n2, Filled = TRUE,
LineColor = RGB::Black,
FillColor = RGB::Red.[0.5]):Наконец, преобразуйте точки p i к графическим точкам и добавьте их в график:
p1 := plot::Point3d(p1, PointColor = RGB::Red,
PointSize = 2*unit::mm):
p2 := plot::Point3d(p2, PointColor = RGB::Red,
PointSize = 2*unit::mm):
plot(s, p1, p2, t1, t2)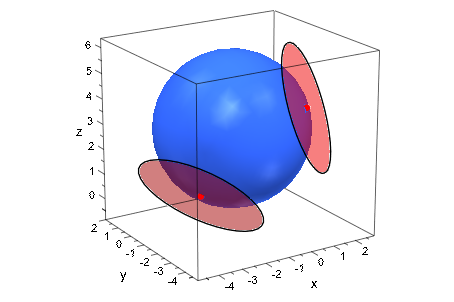
delete c, s, p1, p2, n1, n2, t1, t2:
Рассмотрите ту же сферу как в предыдущем примере:
radius := 3: center := [-1, -1, 5]: s := plot::Sphere(radius, center):
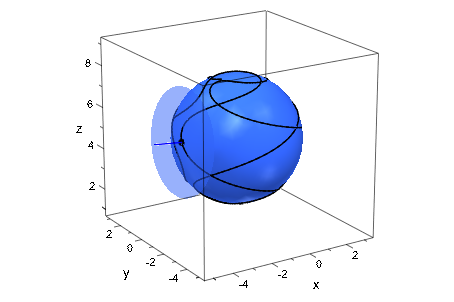
Используя сферические координаты, задайте кривую на сфере:
phi := a -> PI*sin(7*a): thet := a -> PI/2 + 1.3*sin(5*a): x := a -> center[1] + radius*cos(phi(a))*sin(thet(a)): y := a -> center[2] + radius*sin(phi(a))*sin(thet(a)): z := a -> center[3] + radius*cos(thet(a)):
Кривая c задана как объект типа plot::Curve3d. Далее, задайте анимированную точку p, который запускается вдоль кривой. Анимированный заполненный диск типа plot::Circle3d при указании на плоскость касательной в точке p, а также нормальное соответствие добавляется к графику:
c := plot::Curve3d([x(t), y(t), z(t)], t = 0..2*PI,
Mesh = 1000, Color = RGB::Black):
p := a -> [x(a), y(a), z(a)]:
n := a -> zip([x(a), y(a), z(a)], center, _subtract):
d := plot::Circle3d(2.5, p(a), n(a), a = 0..2*PI, Filled = TRUE,
FillColor = RGB::BlueLight.[0.5],
LinesVisible = FALSE):
n := plot::Arrow3d(p(a), [p(a)[i] + n(a)[i]/2 $ i=1..3],
a = 0..2*PI, TipLength = 0.8*unit::mm):
p := plot::Point3d(p(a), a = 0..2*PI, PointColor = RGB::Black,
PointSize = 2*unit::mm):plot(s, c, p, n, d, Frames = 200, TimeEnd = 50):
delete radius, center, s, phi, thet,
x, y, z, c, p, n, d:
|
Радиус сферы: действительное численное значение или арифметическое выражение параметра анимации
|
|
Координаты центра: действительные численные значения или арифметические выражения параметра анимации
|
|
Параметр анимации, заданный как |