`plot`::`Waterman`

Многогранники лодочника

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Waterman(r, <a = a_min .. a_max>, options)

Описание

plot::Waterman(r) создает многогранник Лодочника радиуса r.

Многогранники Уотермена, изобретенные приблизительно 1 990 Стивом Уотерменом, формируют обширное семейство многогранников. У некоторых из них есть много хороших свойств как несколько симметрий или очень интересные и регулярные формы. Некоторый другой - только набор поверхностей, сформированных из неправильных выпуклых многоугольников.

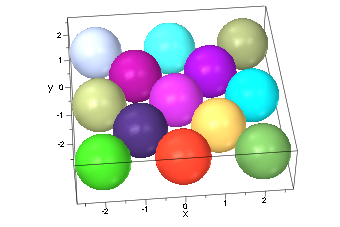
Многогранники лодочника следуют из исследования шаров в гранецентрированной кубической близкой упаковке (который является одной из двух самых плотных упаковок одинаково размерных шаров на 3D пробеле, согласно Догадке Кеплера, проверенной Хейлзом и Фергюсоном, 1997-2005). Единственный слой сфер (радиуса) в этой упаковке выглядит так:

Близкие результаты упаковки размещения нескольких из этих слоев друг по другу, переключенному, чтобы оптимально заполнить разрывы (в почти совершенно также вашем продуктовом магазине помещает яблоки и демонстрирующиеся апельсины):

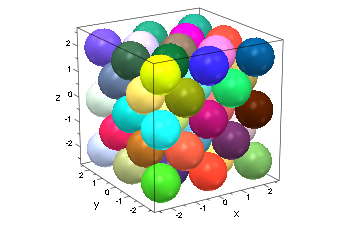
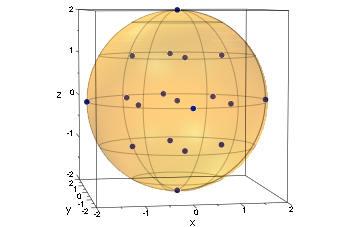
Учитывая радиус r и центр c (который мы позволяем значению по умолчанию к [0, 0, 0]), теперь рассмотрите все те центры сфер в этой упаковке, которые попадают в сферу радиуса r вокруг c:

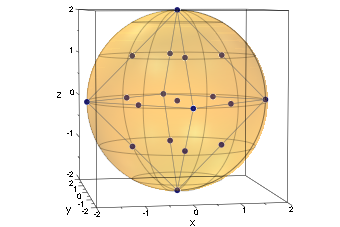
Выпуклая оболочка этих точек является многогранником Лодочника данного радиуса и центра:

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`Center`	центр объектов, центр вращения	[0, 0, 0]
`CenterX`	центр объектов, центр вращения, x-компонент	0
`CenterY`	центр объектов, центр вращения, y-компонент	0
`CenterZ`	центр объектов, центр вращения, z-компонент	0
`Color`	основной цвет	`RGB::SafetyOrange`
`Filled`	заполненные или прозрачные области и поверхности	`TRUE`
`FillColor`	цвет областей и поверхностей	`RGB::SafetyOrange`
`FillColor2`	второй цвет областей и поверхностей для цветных смешений	`RGB::CornflowerBlue`
`FillColorType`	типы заполнения поверхности	`Flat`
`FillColorFunction`	функциональная область / поверхностная окраска
`FillColorDirection`	направление цветовых переходов на поверхностях	[0, 0, 1]
`FillColorDirectionX`	x-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionY`	y-компонент направления цветовых переходов на поверхностях	0
`FillColorDirectionZ`	z-компонент направления цветовых переходов на поверхностях	1
`Frames`	количество систем координат в анимации	50
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`FALSE`
`LineColor`	цвет линий	`RGB::Grey40.[0.4]`
`LineWidth`	ширина линий	0.25
`LineColor2`	цвет линий	`RGB::DeepPink`
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LinesVisible`	видимость линий	`TRUE`
`LineColorType`	типы окраски линии	`Flat`
`LineColorFunction`	функциональная окраска линии
`LineColorDirection`	направление цветовых переходов на линиях	[0, 1, 1]
`LineColorDirectionX`	x-компонент направления цветовых переходов на линиях	0
`LineColorDirectionY`	y-компонент направления цветовых переходов на линиях	1
`LineColorDirectionZ`	z-компонент направления цветовых переходов на линиях	1
`Name`	имя объекта графика (для браузера и легенды)
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`PointSize`	размер точек	1.5
`PointStyle`	стиль презентации точек	`FilledCircles`
`PointsVisible`	видимость точек mesh	`FALSE`
`Radius`	радиус кругов, сферы и т.д.
`Shading`	сглаживайте цветное смешение поверхностей	`Smooth`
`TimeEnd`	время окончания анимации	10.0
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`TitlePositionZ`	положение объектных заголовков, z компонент
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`

Примеры

Пример 1

С увеличивающимся радиусом многогранники Лодочника становятся еще ближе к сферам:

plot(plot::Waterman(r, r=0..10,
                    PointsVisible, PointSize=1,
                    LineColor=RGB::Black,
                    Color=RGB::Red.[0.75]),
     plot::Sphere(r, [0,0,0], r=0..10,
                  Color=RGB::Yellow.[0.3]),
     CameraDirection=[2,10,1])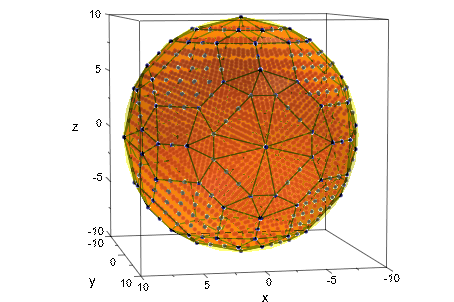

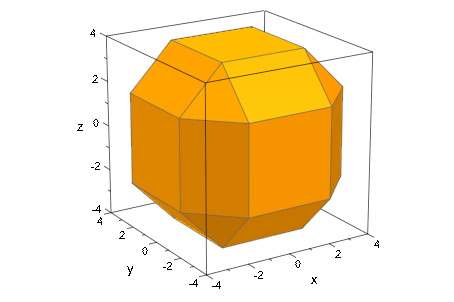
Пример 2

Многогранники лодочника имеют довольно общее определение и могут быть сделаны из сфер, сосредоточенных где угодно:

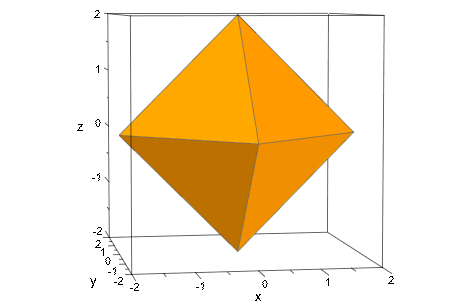
plot(plot::Waterman(5, Center=[0,0,0]))

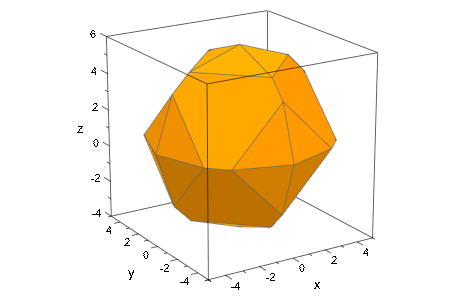
plot(plot::Waterman(5, Center=[0,0,1]))

Чтобы перевести или масштабировать многогранник Лодочника, используйте plot::Translate3d и plot::Scale3d:

n := 3:
r := i -> 3/2+sqrt(i+1):
plot(plot::Translate3d([i mod n, i div n, 0],
               plot::Scale3d([1/(3*r(i)) $ 3],
                  plot::Waterman(r(i), Color=RGB::random())))
     $ i = 0..n^2-1, Axes=None)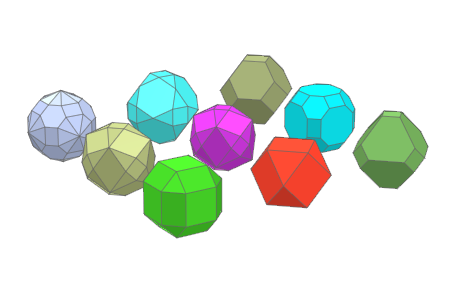

Пример 3

Как обычно, много атрибутов могут быть анимированы, несмотря на то, что по природе многогранников Лодочника, получившаяся анимация не явится гладкой:

plot(plot::Waterman(5, Center=[a/PI, cos(a), 0],
                    a=0..2*PI),
     AnimationStyle=BackAndForth, CameraDirection=[0,0.1,1])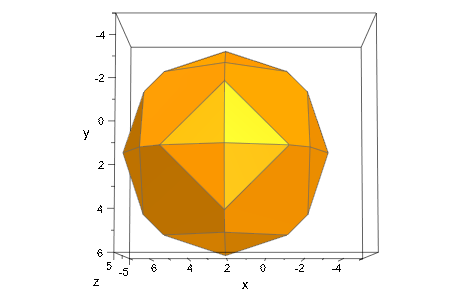

Пример 4

LineColorFunction и FillColorFunction атрибуты могут быть установлены в функции, которые получают индексы в настоящее время нарисованного surfacepolygon и его текущей вершины в качестве четвертого и пятого аргумента, соответственно. Это позволяет окрашивать многоугольники индивидуально:

colors := [RGB::random() $ i = 1..42]:
plot(plot::Waterman(5, FillColorFunction=((x,y,z,i) -> colors[i])))

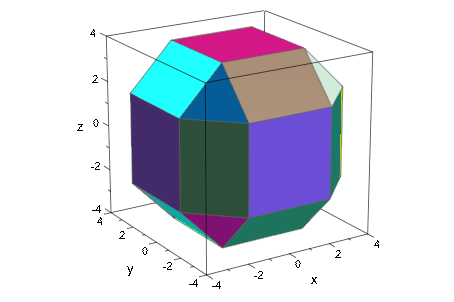
Другой способ получить произвольные цвета, которые остаются постоянными для каждого многоугольника, состоит в том, чтобы использовать процедуру с option remember:

col := 
proc(n)
  option remember;
begin
  RGB::fromHSV([360*frandom(), 1, 1]);
end:
plot(plot::Waterman(7, FillColorFunction=((x,y,z,i) -> col(i))))

Параметры

r

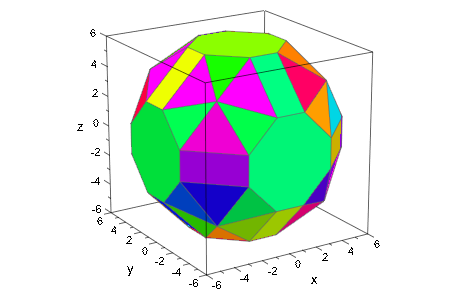
Арифметическое выражение: радиус многогранника (см. ниже для деталей).

r эквивалентно атрибуту Radius.

a

Параметр анимации, заданный как a _{= amin..amax}, где _amin начальное значение параметров и _amax итоговое значение параметров.

Алгоритмы

plot::Waterman использование plot::hull (и поэтому, qhull код Центра Геометрии), чтобы вычислить выпуклую оболочку координат. Большая часть остающегося кода была внесена Миреком Майевским.

Смотрите также

Функции MuPAD

plot

MuPAD графические примитивы

plot::Dodecahedron | plot::Hexahedron | plot::Icosahedron | plot::Octahedron | plot::Sphere | plot::Tetrahedron

Документация