plot::TetrahedronРегулярные тетраэдры
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::Tetrahedron(<a = amin .. amax>, options)
plot::Tetrahedron() создает правильный многогранник.
По умолчанию все многогранники строятся в начале координат. Атрибут Center позволяет задать координаты центра. Это полезно, чтобы выровнять многогранники относительно других объектов в графической сцене. См. Пример 1.
Все многогранники строятся в кубе размерами от-1 до 1 во всех координатных направлениях. Размер многогранников может быть изменен атрибутом RadiusВ случае шестигранника (куба), этот атрибут представляет радиус вписанной сферы. Для других многогранников это - радиус описанной сферы.
Значение по умолчанию Radius 1 для всех многогранников.
В дополнение к атрибутам Center и Radius, можно изменить многогранники путем применения объектов преобразования типа plot::Rotate3d, plot::Scale3d, plot::Translate3d , и plot::Transform3d. См. пример 3.
Пользовательские функции управления цветом (LineColorFunction, FillColorFunction) вызваны индексом текущего фасета как его первый параметр, сопровождаемый x, y и координатой z текущей точки, сопровождаемой текущим значением параметра анимации (если анимировано). См. Пример 4.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
Center | центр объектов, центр вращения | [0 |
CenterX | центр объектов, центр вращения, x-компонент | 0 |
CenterY | центр объектов, центр вращения, y-компонент | 0 |
CenterZ | центр объектов, центр вращения, z-компонент | 0 |
Color | основной цвет | RGB::Red |
Filled | заполненные или прозрачные области и поверхности | TRUE |
FillColor | цвет областей и поверхностей | RGB::Red |
FillColor2 | второй цвет областей и поверхностей для цветных смешений | RGB::CornflowerBlue |
FillColorType | типы заполнения поверхности | Dichromatic |
FillColorFunction | функциональная область / поверхностная окраска | |
FillColorDirection | направление цветовых переходов на поверхностях | [0 |
FillColorDirectionX | x-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionY | y-компонент направления цветовых переходов на поверхностях | 0 |
FillColorDirectionZ | z-компонент направления цветовых переходов на поверхностях | 1 |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Black.[0.25] |
LineWidth | ширина линий | 0.35 |
LineColor2 | цвет линий | RGB::DeepPink |
LineStyle | тело, подчеркнутые штриховой линией или пунктирные линии? | Solid |
LinesVisible | видимость линий | TRUE |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
LineColorDirection | направление цветовых переходов на линиях | [0 |
LineColorDirectionX | x-компонент направления цветовых переходов на линиях | 0 |
LineColorDirectionY | y-компонент направления цветовых переходов на линиях | 0 |
LineColorDirectionZ | z-компонент направления цветовых переходов на линиях | 1 |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
PointSize | размер точек | 1.5 |
PointStyle | стиль презентации точек | FilledCircles |
PointsVisible | видимость точек mesh | FALSE |
Radius | радиус кругов, сферы и т.д. | 1 |
Shading | сглаживайте цветное смешение поверхностей | Smooth |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
TitlePositionZ | положение объектных заголовков, z компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
Используя различный Centers, пять правильных многогранников помещаются рядом друг с другом:
plot(plot::Hexahedron (Center = [0, 0, 0]),
plot::Tetrahedron (Center = [3, 0, 0]),
plot::Octahedron (Center = [6, 0, 0]),
plot::Icosahedron (Center = [9, 0, 0]),
plot::Dodecahedron(Center = [12, 0, 0]),
Axes = Frame);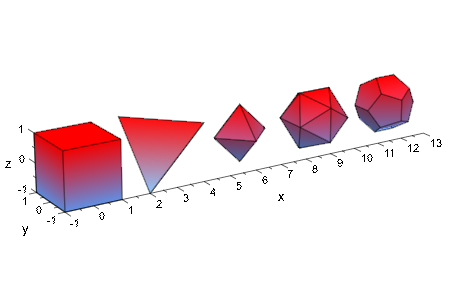
С атрибутом Radius, размер многоугольника может быть изменен:
plot(plot::Hexahedron (Radius = 1.0, Center = [0, 0, 0]),
plot::Tetrahedron (Radius = 1.5, Center = [4, 0, 0]),
plot::Octahedron (Radius = 2.0, Center = [8, 0, 0]),
plot::Icosahedron (Radius = 2.5, Center = [13, 0, 0]),
plot::Dodecahedron(Radius = 3.0, Center = [19, 0, 0]),
Axes = Frame);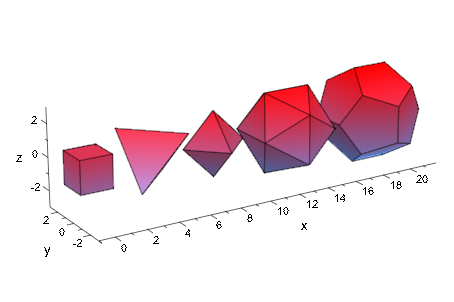
Четырехгранник и октаэдр встраиваются в шестигранник:
plot(plot::Hexahedron (FillColorFunction = RGB::Red.[0.2],
VisibleFromTo = 0..8),
plot::Tetrahedron(FillColorFunction = RGB::Green.[0.2],
VisibleFromTo = 1..5),
plot::Octahedron (FillColorFunction = RGB::Blue.[0.2],
VisibleFromTo = 3..7),
Axes = None)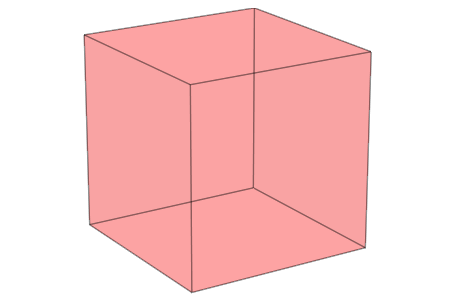
Объекты преобразования могут быть применены к многогранникам, как продемонстрировано ниже:
H := plot::Hexahedron(Color = RGB::Blue.[0.2],
FillColorType = Flat):
T := plot::Tetrahedron(Color = RGB::Red):
plot(plot::Rotate3d(a, [0, 0, 0], [0, 0, 1], a = 0..2*PI,
H,
plot::Translate3d([0, 0, a], T, a = 0..2)
), Axes = None)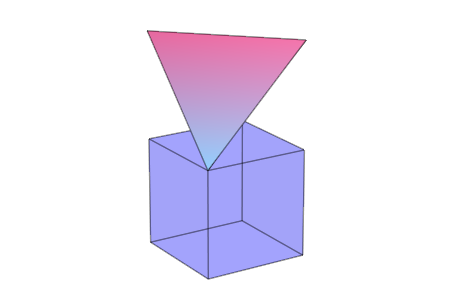
delete T, H:
FillColorFunction может быть задан. Первый параметр при вызове -- индекс текущей грани, далее x -, y - и z - координата текущей точки:
mycolorlist := [RGB::Red, RGB::Blue, RGB::Green, RGB::Yellow]:
plot(plot::Dodecahedron(Center = [0, 0, 0],
FillColorFunction =
proc(n, x, y, z) begin
[(1 + x)/2, (1 + y)/2, (1 + z)/2]
end_proc),
plot::Dodecahedron(Center = [3, 0, 0],
FillColorFunction =
proc(n, x, y, z) begin
mycolorlist[(n mod 4)+1]
end_proc),
Axes = None):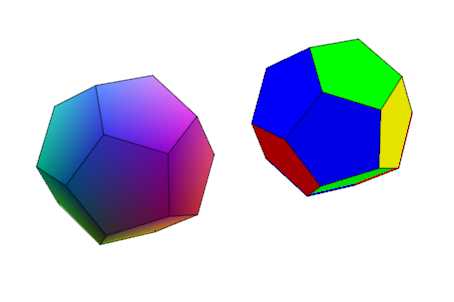
То же самое сохраняется для LineColorFunction:
plot(plot::Icosahedron(Center = [0, 0, 0],
LineColorFunction =
proc(n, x, y, z) begin
[(1 + x)/2, (1 + y)/2, (1 + z)/2]
end_proc),
plot::Icosahedron(Center = [3, 0, 0],
LineColorFunction =
proc(n, x, y, z) begin
mycolorlist[(n mod 4)+1]
end_proc),
Axes = None, LineWidth = 1.0*unit::mm,
FillColor = RGB::Grey80, FillColorType = Flat):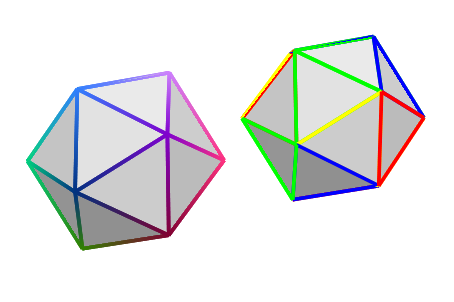
Если многогранник анимирован, функции управления цветом вызваны с дополнительным аргументом: текущее значение параметра анимации:
plot(plot::Octahedron(FillColorFunction =
proc(n, x, y, z, a)
begin
[sin(n*a)^2, cos(n*a)^2, 1]:
end_proc,
a = 0..2*PI))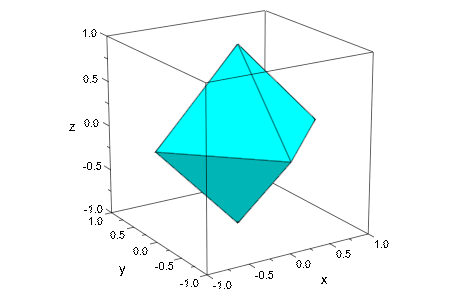
delete mycolorlist:
Многогранник называется правильным, если все его грани состоят из одинаковых правильных многоугольников, и в каждой его вершине сходится одинаковое число рёбер.
Начиная с Платона мы знаем, что существуют только пять правильных многогранников:
четырехгранник с 4 (греческий tetra) треугольники,
шестигранник с 6-тью (по-гречески hexa) квадратами,
октаэдр с 8-ми (по-гречески okta) треугольниками,
додекаэдр с 12-тью (по-гречески dodeka) пятиугольниками
икосаэдр с 20-тью (по-гречески eikosi) треугольниками.
В следующей таблице перечислены некоторые важные геометрические данные многогранников с длиной ребра a. Где R является радиусом внешнего spherem r радиус внутренней сферы, A площадь поверхности и V объем:
| Отношение | Четырехгранник | Шестигранник | Октаэдр | Додекаэдр | Икосаэдр |
|---|---|---|---|---|---|
| 6 | |||||
| 1 |