Документация

Общие решения

Обыкновенное дифференциальное уравнение (ODE) содержит производные зависимых переменных относительно единственной независимой переменной. Если y зависимая переменная и x независимая переменная, решение ОДУ является выражением y(x). Порядок производной зависимой переменной задает порядок ОДУ.

Решение одного явного ОДУ первого порядка может всегда вычисляться интегрированием, предоставил решение, существует. Чтобы задать обыкновенное дифференциальное уравнение, используйте ode команда:

o := ode(y'(x) = y(x)^2, y(x))

Теперь используйте генерала, решают, чтобы решить это уравнение:

solve(o)

В качестве альтернативы можно вызвать решатель ОДУ непосредственно:

ode::solve(y'(x) = y(x)^2, y(x))

Общие решения ОДУ содержат произвольные постоянные интегрирования. Решатель генерирует константы интегрирования с помощью формата прописной буквы C сопровождаемый автоматически сгенерированным номером. Например, это генерирует C1C2 , и так далее.

Для ОДУ высшего порядка можно найти явные решения только для специальных типов уравнений. Например, следующее уравнение второго порядка имеет решение в терминах элементарных функций:

ode::solve(y''(x) = y(x), y(x))

Решатель вводит решение следующего уравнения в терминах Функций Бесселя. MuPAD^® использует стандартные математические обозначения в функции Бесселя и других специальных функциях:

ode::solve(y''(x) = y'(x) + y(x)*exp(x), y(x))

Если у вас есть секунда - или ОДУ высшего порядка, нелинейное ОДУ или система ОДУ, символьное решение не всегда существует:

ode::solve(y''(x) = y'(x)^2 + y(x)*exp(x), y(x))

Для ОДУ, которые не могут быть решены символически, попытайтесь использовать числовые решатели.

Задачи с начальными значениями и Краевые задачи

Много проблем в разработке и физике связали дифференциальные уравнения решения с начальными условиями или граничными условиями или обоими. Чтобы задать начальные или граничные условия, создайте набор, содержащий уравнение и условия. Например, утвердите следующую задачу с начальными значениями путем определения ОДУ с начальными условиями:

IVP := ode({y''(x) = y(x), y(0) = 5, y'(0) = 1}, y(x))

Когда вы решаете ОДУ с начальными или граничными условиями, решатель настраивает константы интегрирования, чтобы соответствовать этим условиям:

solve(IVP)

Следующее уравнение имеет и начальные и граничные условия:

ode::solve({y'''(x) = y(x), y(0) = 0, y(5) = 1, y'(0) = 0}, y(x))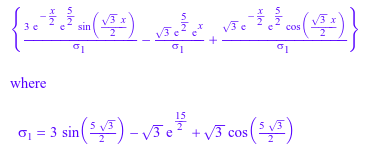

Каждое независимое условие удаляет одно постоянное интегрирование:

ode::solve({y'''(x) = y'(x)}, y(x))

ode::solve({y'''(x) = y'(x), y(0) = 0}, y(x))

ode::solve({y'''(x) = y'(x), y(0) = 0, y(1) = 1}, y(x))

ode::solve({y'''(x)=y'(x), y(0)=0, y(1)=1, y'(0)=1/2}, y(x))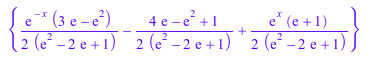

Специальные типы Обыкновенных дифференциальных уравнений

Предположим, уравнение, которое вы хотите решить, принадлежит типу Клеро:

o:= ode(y(x) = x*y'(x) + y'(x)^3, y(x)):
solve(o)

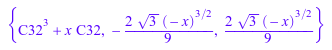
Решатель распознает тип уравнения и применяет алгоритм для решения уравнений Клеро. Чтобы улучшать производительность, вызовите решатель с опцией Type = Clairaut:

solve(o, Type = Clairaut)

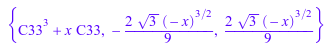
Решатель пытается распознать и пытается решить следующие классы ОДУ.

Ввод	Уравнение	Опция решателя ОДУ
Дифференциальное уравнение Абеля		Абель
Бернуллиевое дифференциальное уравнение	где n ≠ 0 и n ≠ 1	Бернулли
Дифференциальное уравнение Chini		Chini
Дифференциальное уравнение Клеро		Клеро
Точное обыкновенное дифференциальное уравнение первого порядка	это может быть представлено как M (x, y)  dx + N (x, y)  dy = 0 где	ExactFirstOrder
Точное обыкновенное дифференциальное уравнение второго порядка	, если первый интеграл превращает это уравнение в ОДУ первого порядка	ExactSecondOrder
Линейное гомогенное обыкновенное дифференциальное уравнение	Dy = 0, где D линейный дифференциальный оператор	Гомогенный
Лагранжево дифференциальное уравнение		Лагранж
Дифференциальное уравнение Riccati		Riccati

Если решатель не может идентифицировать уравнение с типом, вы указали, это выдает предупреждение и возвращает специальное значение FAIL:

ode::solve(y'(x) + y(x) = x, y(x), Type = Homogeneous)

Warning: Unable to detect homogeneous ODE. [ode::homogeneous]

Системы Обыкновенных дифференциальных уравнений

Чтобы решить систему дифференциальных уравнений, задайте систему как набор уравнений:

s := {y'(x) = z(x), z'(x) = y(x) + 2*z(x)}:

Вызовите ode::solve функция, задающая набор функций {y (x), z (x)}, для которого вы хотите решить систему:

ode::solve(s, {y(x), z(x)})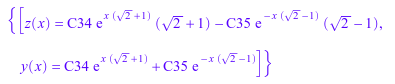

Теперь предположите, что система дифференциальных уравнений появляется в матричной форме. Например, задайте систему, где AB, и Y представляйте следующие матрицы:

Y:= matrix([x(t), y(t)]):
A:= matrix([[1, 2], [-1, 1]]):
B:= matrix([1, t]):

ode::solve функция не принимает матрицы. Чтобы смочь использовать этот решатель, извлеките компоненты матрицы и включайте их в набор. Используйте op функционируйте, чтобы извлечь уравнения из матрицы. Затем используйте фигурные скобки, чтобы создать набор уравнений. Можно не использовать правые стороны уравнений, в этом случае MuPAD принимает их, чтобы быть 0:

s := {op(diff(Y, t) - A*Y - B)}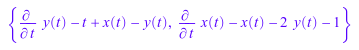

Теперь задайте набор функций {x (t), y (t)}, для которого вы хотите решить систему. Решите систему:

ode::solve(s, {x(t), y(t)})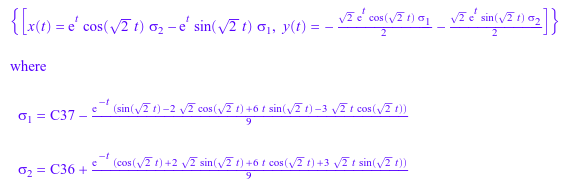

Если вы решаете несколько аналогичных систем обыкновенных дифференциальных уравнений в матричной форме, создаете ваш собственный решатель для этих систем, и затем используете его в качестве ярлыка. Решатель для таких систем должен быть функцией, которая принимает матрицы как входные параметры, и затем выполняет все необходимые шаги. Например, создайте решатель для системы линейных дифференциальных уравнений первого порядка в матричной форме, где компоненты функций зависят от переменной t:

solveLinearSystem := (A, B, Y) ->
solve(ode({op(diff(Y, t) - A*Y - B)}, {op(Y)})):

solveLinearSystem функция принимает матрицы как входные параметры, создает матрицу уравнений, извлекает эти уравнения к набору и решает систему:

Y:= matrix([x(t), y(t)]):
A:= matrix([[1, 2], [-3, 1]]):
B:= matrix([2, t]):
solveLinearSystem(A, B, Y)

Постройте решения дифференциальных уравнений

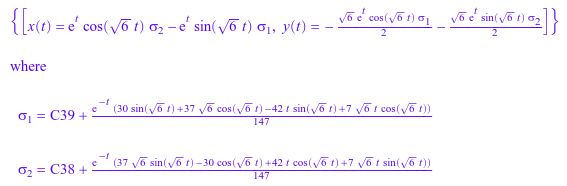
Предположим, что вы хотите решить следующее уравнение. Решатель возвращает результаты как набор, даже если набор содержит только один элемент:

f := ode::solve({y''(x) = x*y'(x), y(0) = 0, y'(0) = 1/3}, y(x))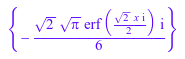

Функции построения графика в MuPAD не принимают наборы. Чтобы построить решение, получите доступ к элементам набора решения с помощью квадратных скобок или op команда:

plotfunc2d(f[1], x = -3..3)

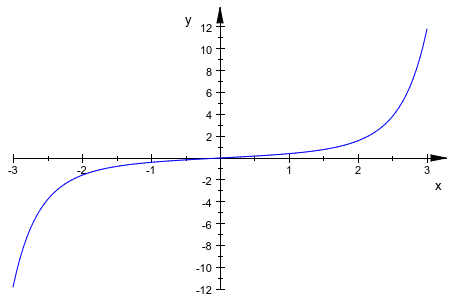
Если у вас есть больше чем один элемент набора решения, можно получить доступ к конкретному элементу. Например, выберите второй элемент набора решения для системы ОДУ:

f := ode::solve(
               {y'(x) = z(x), z'(x) = y(x) + 2*z(x),
                y(0) = 0, z(0) = 1}, {y(x), z(x)})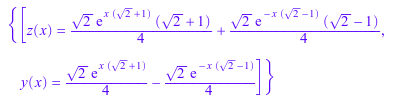

Решатель возвращает результаты для системы как набор, который содержит список. Чтобы открыть набор и получить доступ к списку, используйте квадратные скобки или op команда. Чтобы получить доступ к конкретной записи этого списка, используйте квадратные скобки:

f[1][2];
op(f)[2]

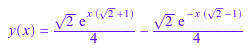
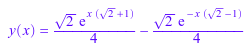
Чтобы получить доступ к правой стороне уравнения, используйте квадратные скобки или rhs команда:

f[1][2][2];
rhs(f[1][2])

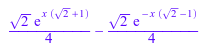
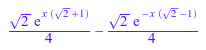
Постройте это решение:

plotfunc2d(f[1][2][2], x = -1..1)

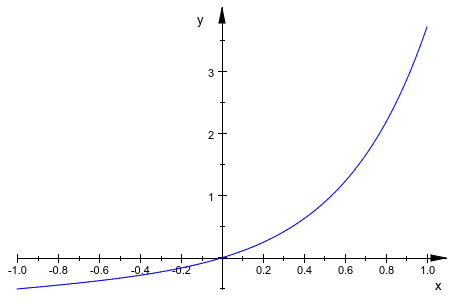
Чтобы построить решение системы ОДУ в 3-D, используйте plot::Curve3d команда:

solution := plot::Curve3d([x, f[1][2][2], f[1][1][2]],
                              x = -2..2, GridVisible):
plot(solution)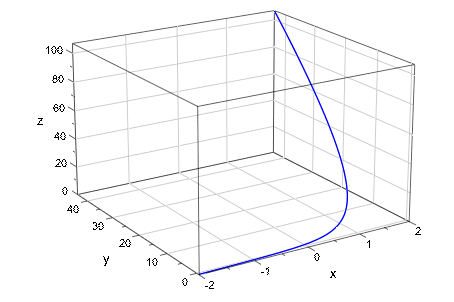

MuPAD предоставляет функциям plot::Ode2d и plot::Ode3d для визуализации решений ОДУ. Кроме того, можно построить векторное поле, сопоставленное с ОДУ. Для всех графических возможностей, доступных в MuPAD, смотрите Графику и Анимации.