plot::VectorField2d2D векторное поле
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
plot::VectorField2d([v1, v2],x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options) plot::VectorField2d(v1,v2,x = xmin .. xmax,y = ymin .. ymax, <a = amin .. amax>,options)
plot::VectorField2d([v_1, v_2], x = `x_{min}`..`x_{max}`, y = `y_{min}`..`y_{max}`) представляет график векторного поля, заданного
с (x, y) ∈ [x m in, x m ax] × [y m in, y m ax].
Векторное поле задано функцией
. plot::VectorField2d отображает векторное поле путем размещения стрел равномерно стрелкой в (x, y) указывающий в направлении f (x, y).
Длина стрел зависит от |f (x, y) | и установка атрибута ArrowLength: По умолчанию длины стрелы пропорциональны величине f, но могут собираться быть фиксированной длины или масштабироваться логарифмически.
Плотностью помещенных стрел можно управлять с атрибутами XMesh, YMesh, и Mesh. Смотрите примеры ниже.
| Атрибут | Цель | Значение по умолчанию |
|---|---|---|
AffectViewingBox | влияние объектов на ViewingBox из сцены | TRUE |
AntiAliased | сглаженные линии и точки? | TRUE |
ArrowLength | масштабирование стрелок в векторном поле | Proportional |
Color | основной цвет | RGB::Blue |
Frames | количество систем координат в анимации | 50 |
Legend | делает запись легенды | |
LegendText | короткий объяснительный текст для легенды | |
LegendEntry | добавить этот объект в легенду? | FALSE |
LineColor | цвет линий | RGB::Blue |
LineWidth | ширина линий | 0.35 |
LineColor2 | цвет линий | RGB::DeepPink |
LineColorType | типы окраски линии | Flat |
LineColorFunction | функциональная окраска линии | |
LineColorDirection | направление цветовых переходов на линиях | [0 |
LineColorDirectionX | x-компонент направления цветовых переходов на линиях | 0 |
LineColorDirectionY | y-компонент направления цветовых переходов на линиях | 1 |
Mesh | количество точек выборки | [11 |
Name | имя объекта графика (для браузера и легенды) | |
ParameterEnd | закончите значение параметра анимации | |
ParameterName | имя параметра анимации | |
ParameterBegin | начальное значение параметра анимации | |
ParameterRange | область значений параметра анимации | |
TimeEnd | время окончания анимации | 10.0 |
TimeBegin | время начала анимации | 0.0 |
TimeRange | оперативный промежуток анимации | 0.0 |
TipAngle | вводный угол наконечников стрелки | 0.6283185307 |
TipStyle | стиль презентации наконечников стрелки | Open |
TipLength | длина наконечников стрелки | 1.5 |
Title | объектный заголовок | |
TitleFont | шрифт объектных заголовков | [" sans-serif ", 11 |
TitlePosition | положение объектных заголовков | |
TitleAlignment | выравнивание по горизонтали заголовков w.r.t. их координаты | Center |
TitlePositionX | положение объектных заголовков, x компонент | |
TitlePositionY | положение объектных заголовков, y компонент | |
Visible | видимость | TRUE |
VisibleAfter | объект, видимый после этой временной стоимости | |
VisibleBefore | объект, видимый до этой временной стоимости | |
VisibleFromTo | объект, видимый в это время, располагается | |
VisibleAfterEnd | объект, видимый после его законченного времени анимации? | TRUE |
VisibleBeforeBegin | объект, видимый перед его временем анимации, запускается? | TRUE |
XFunction | функция для x значений | |
XMax | окончательное значение параметра “x” | |
XMesh | количество точек выборки для параметра “x” | 11 |
XMin | начальное значение параметра “x” | |
XName | имя параметра “x” | |
XRange | область значений параметра “x” | |
YFunction | функция для y значений | |
YMax | окончательное значение параметра “y” | |
YMesh | количество точек выборки для параметра “y” | 11 |
YMin | начальное значение параметра “y” | |
YName | имя параметра “y” | |
YRange | область значений параметра “y” |
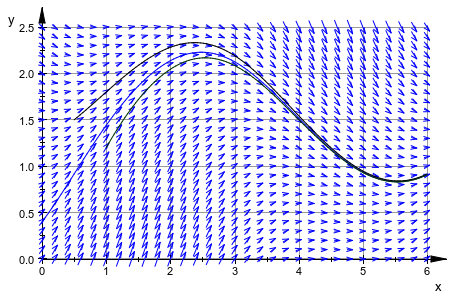
Мы демонстрируем график векторного поля v (x, y) = (1, sin (x) + cos (y)):
field := plot::VectorField2d([1, sin(x) + cos(y)],
x = 0..6, y = 0..2.5,
Mesh = [31, 26]):Это - поле направлений, сопоставленное с одой
. Мы вставляем кривые, представляющие числовые решения этой оды в этот график. Мы используем numeric::odesolve2 вычислить числовые решения для начальных значений y (0) = 0.4, y (0.5) = 1.5, и y (1) = 1.2:
f := (x, y) -> [sin(x) + cos(y[1])]:
solution1 := numeric::odesolve2(f, 0, [0.4]):
curve1 := plot::Function2d(solution1(x)[1], x = 0 .. 6,
LineColor = RGB::Blue):
solution2 := numeric::odesolve2(f, 0.5, [1.5]):
curve2 := plot::Function2d(solution2(x)[1], x = 0.5 .. 6,
LineColor = RGB::Black):
solution3 := numeric::odesolve2(f, 1, [1.2]):
curve3 := plot::Function2d(solution3(x)[1], x = 1 .. 6,
LineColor = RGB::GreenDark):Мы строим три объекта в одной графической сцене:
plot(field, curve1, curve2, curve3, GridVisible = TRUE):
delete field, curve1, curve2, curve3:
Примите, что вы хотите построить электростатическое потенциальное поле. Следующая стандартная программа генерирует необходимую формулу в формате, принятом plot::VectorField2d:
potentialE :=
proc(l)
local p, x0, y0, f0, fx, fy, dist;
begin
fx := 0; fy := 0;
for p in [args()] do
[x0, y0, f0] := p;
dist := sqrt((x-x0)^2 + (y-y0)^2);
fx := fx + f0*(x-x0)/dist;
fy := fy + f0*(y-y0)/dist;
end_for;
[fx, fy];
end_proc:plot(plot::VectorField2d(potentialE([-1, -2, -1 ],
[ 1, 3, 0.5],
[ 2, -1, 0.5]),
x = -3..3, y = -3..3,
XMesh = 30, YMesh = 30)):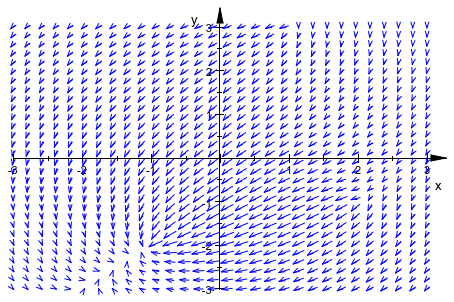
Как большинство других объектов, plot::VectorField2d может быть анимирован путем предоставления дополнительного параметра:
field := plot::VectorField2d([1, a*sin(x) + (a-1)*cos(y)],
x = 0..6, y = 0..2.5, a=-1..1):
text := plot::Text2d(a -> "a = ".stringlib::formatf(a, 2, 5), [2, -0.5],
a = -1..1, HorizontalAlignment = Left):
plot(field, text)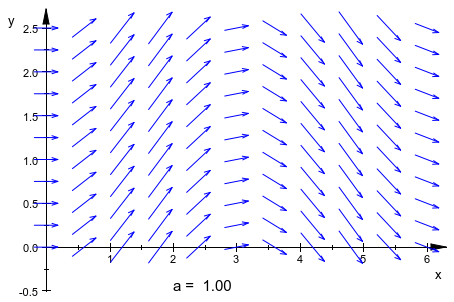
delete field, text:
|
x - и y - компонент векторного поля: арифметические выражения в |
|
Идентификаторы. |
|
Действительные численные значения.
|
|
Параметр анимации, заданный как |