Пакетное 2D разложение вейвлета
T = wpdec2(X,N,wname,E,P)
T = wpdec2(X,N,wname)
T = wpdec2(X,N,wname,'shannon')
wpdec2 двумерная пакетная аналитическая функция вейвлета.
T = wpdec2(X,N, возвращает пакетное дерево вейвлета wname,E,P)T соответствие пакетному разложению вейвлета матричного X, на уровне N, с заданным вейвлетом wname (см. wfilters для получения дополнительной информации.
T = wpdec2(X,N, эквивалентно wname)T = wpdec2(X,N,.wname,'shannon')
E вектор символов или скаляр строки, содержащий тип энтропии и P дополнительный параметр в зависимости от значения T (см. wentropy для получения дополнительной информации.
| Энтропийное имя типа (E) | Параметр (P) | Комментарии |
|---|---|---|
'shannon' | P не используется. | |
'log energy' | P не используется. | |
'threshold' | 0P | P порог. |
'sure' | 0P | P порог. |
'norm' | 1P | P степень. |
'user' | Вектор символов или скаляр строки | P вектор символов или скаляр строки, содержащий имя файла вашей собственной энтропийной функции, с одним входом X. |
FunName | Никакие ограничения на P |
|
'user' опция является исторической и все еще сохраненная для совместимости, но это - obsoleted последней опцией, описанной в предыдущей таблице. FunName опция делает то же самое как 'user' опция и кроме того, позволяет вам передавать параметр своей собственной энтропийной функции.
Смотрите wpdec для большего количества полного описания пакетного разложения вейвлета.
% The current extension mode is zero-padding (see dwtmode).
% Load image.
load tire
% X contains the loaded image.
% For an image the decomposition is performed using:
t = wpdec2(X,2,'db1');
% The default entropy is shannon.
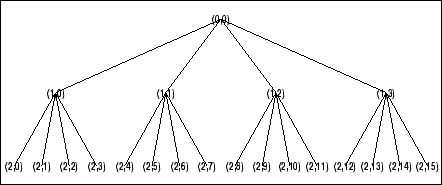
% Plot wavelet packet tree
% (quarternary tree, or tree of order 4).
plot(t)
Когда X представляет индексируемое изображение, X m- n матрица. Когда X представляет изображение истинного цвета, это - m- n- 3 массива, где каждый m- n матрица представляет красную, зеленую, или синюю цветную плоскость, конкатенированную по третьему измерению.
Для получения дополнительной информации о форматах изображения смотрите image и imfinfo страницы с описанием.
Алгоритм, используемый в пакетном разложении вейвлета, следует за той же линией как процесс разложения вейвлета (см. dwt2 и wavedec2 для получения дополнительной информации.
Койфман, R.R.; т-х Викераузер (1992), “Основанные на энтропии алгоритмы для лучшего базисного выбора”, Сделка IEEE на Inf. Теория, издание 38, 2, стр 713–718.
Мейер, Y. (1993), Les ondelettes. Algorithmes и приложения, Колин Эд., Париж, 2-й выпуск. (Английский перевод: Вейвлеты: Алгоритмы и Приложения, SIAM).
Wickerhauser, Т-х (1991), “INRIA читает лекции по пакетным алгоритмам вейвлета”, Продолжения ondelettes и paquets d'ondes, 17-21 июня, Rocquencourt, Франция, стр 31–99.
Wickerhauser, Т-х (1994), Адаптированный анализ вейвлета от теории до программного обеспечения Algorithms, А.К. Питерса.