initialCondition

Начальное представление условия для линейных независимых от времени систем

Описание

initialCondition объект инкапсулирует информацию о начальном условии для модели линейного независимого от времени (LTI). Объект обобщает числовое векторное представление начальных состояний модели в пространстве состояний так, чтобы информация применилась к линейным моделям любой формы — передаточные функции, полиномиальные модели или модели в пространстве состояний.

Можно оценить и получить начальные условия, когда вы идентифицируете линейную модель с помощью команд такой как tfest или сравните ответ модели на измеренное использование данных о вводе/выводе compare. Программное обеспечение оценивает начальное значение условия путем минимизации симуляции или ошибки предсказания против измеренных выходных данных. Можно затем применить те начальные условия в последующей симуляции, с помощью команд такой как sim или predict, подтвердить производительность модели относительно тех же данных об измерении. Используйте initialCondition команда, чтобы создать initialCondition объект из спецификации модели в пространстве состояний или из любой модели LTI свободного ответа.

initialCondition объект может также быть рассмотрен как представление свободного ответа линейной модели. Функции симуляции используют эту информацию, чтобы вычислить ответ модели следующим образом:

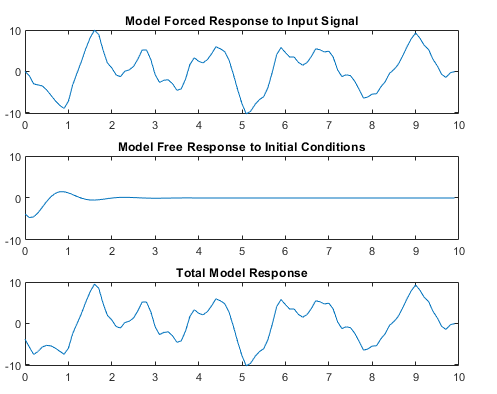
Вычислите принудительный ответ модели к входному сигналу. Принудительный ответ является стандартной симуляцией выход, когда нет никаких заданных начальных условий.
Вычислите импульсную характеристику модели и масштабируйте результат сгенерировать свободный ответ модели к заданным начальным условиям.
Добавьте спрессованный ответ и свободный ответ, чтобы сформировать общий отклик системы.

Фигура иллюстрирует этот процесс.

The top plot shows the forced response. The middle plot shows the free response. The bottom plot shows the total model response that sums the first two plots

Для непрерывных систем (Ts = 0), свободный ответ G (s) для вектора начального состояния _x0

$G (s) = C {(s I - A)}^{- 1} x_{0}$

Здесь, C эквивалентен матрице измерения пространства состояний, C и A эквивалентны состоянию пространства состояний матричный A.

Для дискретных систем (Ts> 0), свободный ответ G (z)

$G (z) = z C {(z I - A)}^{- 1} x_{0}$

initialCondition объект представляет свободный ответ в форме пространства состояний. Объект является структурой со свойствами, содержащими пространство состояний A и матрицы C и вектор начального состояния _x0. Для idtf и idpoly модели, с помощью initialCondition объект является единственным способом представлять и использовать начальные условия для симуляции. Для idss модели, можно использовать любого initialCondition возразите или числовой вектор начального состояния. Когда вы получаете начальные условия ic для данных о мультиэксперименте, ic объектный массив, с одним initialCondition объект для каждого эксперимента.

Создание

Можно получить initialCondition объект одним из четырех способов.

Оценка модели — Указывает, что оценка функциональный возврат предполагаемое начальное условие, которое соответствует данным о вводе/выводе оценки. Например, можно использовать следующую команду, чтобы получить предполагаемое начальное условие ic для модели sys передаточной функции это оценивается с данными о вводе/выводе z.
```
[sys,ic] = tfest(z,2,1)
```
Для примера смотрите, Получают Предполагаемые Начальные условия.
Сравнение модели к данным с помощью любых данных о вводе/выводе — Задает это compare возвратите предполагаемое начальное условие, которое функция оценивает внутренне, чтобы поддержать fit оценка. Например, можно использовать следующую команду, чтобы получить начальное условие ic для линейной модели sys при определении подгонки против данных о вводе/выводе zyp симулированный или предсказал выход модели.
```
[yp,fit,ic] = compare(z,sys)
```
Для примера смотрите, Получают Начальные условия для Новых Данных.
Прямая конструкция — Использование initialCondition команда, чтобы инкапсулировать форму пространства состояний модели свободного ответа в initialCondition объект.
```
ic = initialCondition(A,X0,C,Ts)
```
Для примера смотрите Построение initialCondition Объект от Модели в пространстве состояний.
Преобразование модели свободного ответа — Использование initialCondition команда, чтобы преобразовать модель свободного ответа LTI в initialCondition объект.
```
ic = initialCondition(G)
```
Для примера смотрите, Преобразуют Модель Свободного Ответа в Объект initialCondition.

Для получения информации о функциях можно использовать, чтобы извлечь информацию из или преобразовать initialCondition объекты, см. Функции объекта.

Синтаксис

ic = initialCondition(A,X0,C,Ts)

ic = initialCondition(G)

Описание

пример

ic = initialCondition(A,X0,C,Ts) создает initialCondition объект, который представляет свободный ответ на начальное условие, описанное в форме пространства состояний, модели LTI.

$\begin{array}{l} d x = A x \\ y = C x \\ x (0) = x_{0} \end{array}$

ic хранилища эта модель в форме свойств. A и C соответствуйте реализации пространства состояний модели, X0 к вектору начального состояния _x0 и Ts к шагу расчета. Можно использовать ic задавать начальные условия при симуляции любого типа системы LTI.

пример

ic = initialCondition(G) создает initialCondition объект, соответствующий линейной модели G из свободного ответа.

Входные параметры

развернуть все

`G` — Модель свободного ответа
Модель LTI

Модель свободного ответа в виде модели LTI без входных параметров. В случае непрерывного времени, G должно быть строго соответствующим. В случае дискретного времени, G должен быть biproper. Для примера использования модели свободного ответа, чтобы получить initialCondition возразите, смотрите, Преобразуют Модель Свободного Ответа в Объект initialCondition.

Свойства

развернуть все

`A` — матрица A реализации пространства состояний LTI свободный ответ
числовая матрица

Матрица A реализации пространства состояний LTI свободный ответ в виде _Nx-by-_Nx числовая матрица, где _Nx является количеством состояний. Для примера использования этого свойства смотрите, Получают Предполагаемые Начальные условия.

`X0` — Начальные состояния реализации пространства состояний LTI свободный ответ
числовой вектор

Начальные состояния реализации пространства состояний LTI свободный ответ в виде числового вектора из длины _Nx. Для примера использования этого свойства смотрите, Получают Предполагаемые Начальные условия.

`C` — матрица C реализации пространства состояний LTI свободный ответ
числовая матрица

Матрица C реализации пространства состояний LTI свободный ответ в виде _Ny-by-_Nx числовая матрица, где _Ny является количеством выходных параметров. Для примера использования этого свойства смотрите, Получают Предполагаемые Начальные условия.

`Ts` Размер шага
0 | –1 | положительная скалярная величина

Шаг расчета LTI свободный ответ в виде одного из следующего:

Модель непрерывного времени — 0
Модель дискретного времени с заданным временем выборки — Положительная скалярная величина, представляющая период выборки, описанный в модуле, задана TimeUnit свойство модели
Модель дискретного времени с незаданным шагом расчета — –1

Шаг расчета initialCondition объект эквивалентен для модели динамической системы, которой соответствует объект.

Функции объекта

Функции, применимые к initialCondition объекты - те, которые могут возвратиться, использовать или преобразовать объекты.

Роль Начального условия (IC)	Тип функции LTI	Пример синтаксиса	Ссылки в качестве примера
Возвратите оцененные объекты IC	Все функции оценки, `compare`	`[sys,ic] = tfest(data,2,1)`	Получите предполагаемые начальные условия Получите начальные условия для данных о мультиэксперименте Получите начальные условия для новых данных
Используйте объекты IC для ответа модели	Опция устанавливает для функций отклика модели	`opt = simOptions('InitialCondition',ic)`	Примените начальные условия в симуляции
Преобразуйте объекты IC в Модели Динамической системы (DSMs)	Функции объекта DSM	`g = idtf(ic)`	Визуализируйте свободный ответ на начальное условие
Анализируйте модели, преобразованные от объектов IC	Аналитические функции DSM	`y_g = impulse(g)`	Визуализируйте свободный ответ на начальное условие

развернуть все

Оцените и возвратите начальные условия

`tfest`	Оцените передаточную функцию
`procest`	Оцените модель процесса, использующую данные о частоте или время
`arx`	Оцените параметры ARX, ARIX, AR или модели ARI
`armax`	Оцените параметры ARMAX, ARIMAX, ARMA или модели ARIMA с помощью данных временного интервала
`bj`	Оцените модель полинома Поля-Jenkins, использующую данные об области времени
`oe`	Оцените модель полинома ошибки на выходе с помощью данных частотного диапазона или временного интервала
`polyest`	Оцените полиномиальную модель, использующую время - или данные частотного диапазона
`compare`	Сравните идентифицированный выход модели и измеренный выход

Используйте начальные условия

`sim`	Симулируйте ответ идентифицированной модели
`simOptions`	`Набор опций для sim`
`predict`	Предскажите ошибочную ковариацию оценки состояния и оценки состояния на следующем временном шаге с помощью сигма-точечного фильтра Калмана или фильтра частиц
`predictOptions`	Опция установлена для `predict`
`pe`	Ошибка предсказания для идентифицированной модели
`peOptions`	Набор опции для `pe`
`resid`	Вычислите и протестируйте остаточные значения
`residOptions`	`Набор опций для resid`
`compare`	Сравните идентифицированный выход модели и измеренный выход
`compareOptions`	Набор опции для `compare`

Преобразуйте начальные условия в модель динамической системы

`idss`	Модель в пространстве состояний идентифицируемыми параметрами
`idpoly`	Полиномиальная модель идентифицируемыми параметрами
`idtf`	Модель передаточной функции идентифицируемыми параметрами

Анализируйте Свободный Ответ Модели с помощью `idss` Форма

`impulse`	График импульсной характеристики динамической системы; данные об импульсной характеристике
`freqresp`	Частотная характеристика по сетке

Примеры

свернуть все

Получите предполагаемые начальные условия

Скрипт Open Live Script

Оцените модель передаточной функции и получите оцененные начальные условия.

Загрузите и отобразите данные на графике.

load iddata1ic.mat z1i
plot(z1i)

Выходные данные не запускаются в 0.

Оцените передаточную функцию второго порядка sys_tf. Укажите что функциональный возврат начальные условия ic.

[sys_tf,ic] = tfest(z1i,2,1);

Исследуйте содержимое icic включает, в форме пространства состояний, свободная модель ответа, заданная матрицами A и C, вектор начального состояния X0, и шаг расчета Ts.

A = ic.A

A = 2×2

   -2.9841   -5.5848
    4.0000         0

C = ic.C

C = 1×2

    0.2957    5.2441

x0 = ic.X0

x0 = 2×1

   -0.9019
   -0.6161

Ts = ic.Ts

Ts = 0

ic характерно для данных об оценке z1i. Можно использовать ic установить начальные условия, когда вы симулируете любую модель LTI с помощью входного сигнала от z1i и сравните ответ с z1i выходной сигнал.

Визуализируйте свободный ответ на начальное условие

Скрипт Open Live Script

Визуализируйте свободный ответ, инкапсулировавший в initialCondition объект путем генерации импульсной характеристики.

Оцените передаточную функцию и возвратите начальное условие ic_tf.

load iddata1ic z1i
[sys_tf,ic_tf] = tfest(z1i,2,1);
ic_tf

ic_tf = 
  initialCondition with properties:

     A: [2x2 double]
    X0: [2x1 double]
     C: [0.2957 5.2441]
    Ts: 0

ic_tf содержит информацию, необходимую, чтобы вычислить свободный ответ на начальное условие.

Преобразуйте ic_tf в idss объект, который может быть передан impulse функция.

ic_tfss = idss(ic_tf);

Создайте временной вектор t это охватывает набор данных. Вычислите импульсную характеристику.

t = 0:0.1:9.9;
t = t';
yimp = impulse(ic_tfss,t);
plot(t,yimp)
title('Free Response to Initial Condition')

Свободный ответ является переходным процессом, который продержался в течение приблизительно четырех секунд.

Примените начальные условия в симуляции

Скрипт Open Live Script

Загрузите данные и оцените передаточную функцию второго порядка sys. Возвратите начальные условия в ic.

load iddata1ic z1i
[sys,ic] = tfest(z1i,2,1);

Симулируйте sys использование данных об оценке, но не включая начальное условие. Постройте симулированный выход с измеренным выходом.

y_no_ic = sim(sys,z1i);
plot(y_no_ic,z1i)
legend('Model Response','Measured Output')

Измеренные и симулированные выходные параметры не соглашаются в начале симуляции.

Включите ic в simOptions опция установила opt. Симулируйте и постройте ответ модели с помощью opt.

opt = simOptions('InitialCondition',ic);
y_ic = sim(sys,z1i,opt);
plot(y_ic,z1i);
legend('Model Response','Measured Output')

Симуляция комбинирует ответ модели на входной сигнал со свободным ответом на начальное условие. Измеренные и симулированные выходные параметры теперь имеют лучшее соглашение в начале симуляции.

Получите начальные условия для новых данных

Скрипт Open Live Script

Предполагаемый initialCondition объект характерен для данных, из которых вы оценили его. Если вы хотите симулировать свою модель с новыми данными, такими как данные о валидации, необходимо оценить новое начальное условие для тех данных. Для этого используйте compare команда.

Загрузите данные и разделите их в наборы данных оценки и валидации.

load iddata1 z1
z1_est = z1(1:150);
z1_val = z1(151:300);
plot(z1_est,z1_val);
legend('Estimation Data','Validation Data')

Исследуйте стартовые точки каждого набора выходных данных.

e0 = z1_est.y(1)

e0 = -0.5872

v0 = z1_val.y(1)

v0 = -7.4390

Эти два набора данных имеют различные стартовые условия.

Оцените модель передаточной функции второго порядка использование z1_est. Возвратите предполагаемые начальные условия в ic_est. Отобразите X0 свойство ic_est. Это свойство представляет предполагаемый вектор начального состояния что модель свободного ответа, заданная ic_est.A и ic_est.C отвечает на.

[sys,ic_est] = tfest(z1_est,2,1);
ic_est.X0

ans = 2×1

   -0.4082
    0.0095

Можно использовать ic_est если вы хотите симулировать sys использование z1_est. В качестве альтернативы можно использовать compare, который оценивает начальное условие независимо. Используйте compare дважды, однажды чтобы отобразить данные на графике и однажды возвращать результаты. Отобразите вектор начального состояния ic_estc.X0 тот compare оценки.

compare(z1_est,sys)

[yce,fit,ic_estc] = compare(z1_est,sys);
ic_estc.X0

ans = 2×1

   -0.4082
    0.0095

Вектор начального состояния ic_estc.X0 идентично ic_est.

Теперь оцените модель с набором данных валидации. Оцените начальные условия с данными о валидации.

compare(z1_val,sys)

[ycv,fit,ic_valc] = compare(z1_val,sys);
ic_valc.X0

ans = 2×1

   -1.7536
   -0.9547

Можно использовать ic_val когда вы симулируете sys с z1_val входной сигнал и сравнивает ответ модели на z1_val выходной сигнал.

Получите начальные условия для данных о мультиэксперименте

Скрипт Open Live Script

Оцените initialCondition объектный массив с помощью данных о мультиэксперименте.

Загрузите данные из двух экспериментов. Объедините эти два набора данных в один набор данных мультиэксперимента.

load iddata1 z1
load iddata2 z2
z12 = merge(z1,z2)

z12 =
Time domain data set containing 2 experiments.

Experiment   Samples      Sample Time          
   Exp1         300            0.1             
   Exp2         400            0.1             
                                               
Outputs      Unit (if specified)               
   y1                                          
                                               
Inputs       Unit (if specified)               
   u1

plot(z12)

Оцените передаточную функцию второго порядка sys и возвратите начальные условия в ic.

np = 2;
nz = 1;
[sys,ic] = tfest(z12,np,nz);
ic

ic=1×2 object
  1x2 initialCondition array with properties:

    A
    X0
    C
    Ts

ic объектный массив. Отобразите содержимое каждого объекта.

ic(1,1)

ans = 
  initialCondition with properties:

     A: [2x2 double]
    X0: [2x1 double]
     C: [-0.7814 5.2530]
    Ts: 0

ic(1,2)

ans = 
  initialCondition with properties:

     A: [2x2 double]
    X0: [2x1 double]
     C: [-0.7814 5.2530]
    Ts: 0

Сравните Ax0 , и C свойства для каждого объекта.

A1 = ic(1,1).A

A1 = 2×2

   -3.4824   -5.5785
    4.0000         0

A2 = ic(1,2).A

A2 = 2×2

   -3.4824   -5.5785
    4.0000         0

C1 = ic(1,1).C

C1 = 1×2

   -0.7814    5.2530

C2 = ic(1,2).C

C2 = 1×2

   -0.7814    5.2530

X01 =ic(1,1).X0

X01 = 2×1

   -0.6528
   -0.0067

X02 =ic(1,2).X0

A и C матрицы идентичны. Эти матрицы представляют форму пространства состояний sys. X0 векторы отличаются. Это различие следует из различных начальных условий для двух экспериментов.

Создайте `initialCondition` Объект от модели в пространстве состояний

Скрипт Open Live Script

Оцените модель в пространстве состояний и возвратите начальные состояния. Из модели и вектора начального состояния, создайте initialCondition объект, который может использоваться с любой линейной моделью.

Загрузите и отобразите данные на графике.

load iddata1ic z1i
plot(z1i)

Оцените модель в пространстве состояний и получите предполагаемые начальные условия.

Во-первых, установите 'InitialState' аргумент пары "имя-значение" в ssestOptions к 'estimate', который заменяет настройку по умолчанию 'auto'. 'estimate' установка всегда оценивает начальные состояния. 'auto' установка использует 'zero' установка, если эффект начальных состояний на полной ошибке расчета модели относительно мал и может поэтому привести к вектору начального состояния, содержащему только нули.

opt = ssestOptions;
opt = ssestOptions('InitialState','estimate');

Оцените модель в пространстве состояний второго порядка sys_ss. Задайте выходной аргумент x0 возвратить вектор начального состояния. Задайте входной параметр opt использовать ваш 'InitialState' установка. После оценки исследуйте x0.

[sys_ss,x0] = ssest(z1i,2,opt);
x0

x0 ненулевой вектор начального состояния.

Симулируйте модель с помощью x0 и сравните выход с исходными выходными данными.

Использовать x0 как начальное условие, задайте 'InitialCondition' аргумент пары "имя-значение" в simOptions как x0.

opt = simOptions;
opt = simOptions('InitialCondition',x0);

Симулируйте модель с помощью opt и сохраните ответ в xss.

xss = sim(sys_ss,z1i,opt);

Постройте ответ модели с исходными выходными данными.

t = 0:0.1:19.9;
plot(t',[xss.y z1i.y])
legend('ss model','output data')
title('Simulated State-Space Model Using Estimated Initial States')

Симуляция запускается в точке близко к начальной точке данных.

С A и C матрицы, x0, и шаг расчета Ts от sys_ss, создайте initialCondition объект ic то, что можно использовать с моделью передаточной функции.

A = sys_ss.A;
C = sys_ss.C;
Ts = sys_ss.Ts;
ic = initialCondition(A,x0,C,Ts)

ic = 
  initialCondition with properties:

     A: [2x2 double]
    X0: [2x1 double]
     C: [-61.3674 13.4811]
    Ts: 0

Оцените модель передаточной функции и симулируйте модель с помощью ic как начальное условие. Сохраните ответ в xtf.

sys_tf = tfest(z1i,2,1);
opt = simOptions('InitialCondition',ic);
xtf = sim(sys_tf,z1i,opt);

Постройте ответы модели xss и xtf вместе.

plot(t',[xss.y xtf.y])
legend('ss model','tf model')
title('Simulated SS and TF Models with Equivalent Initial Conditions')

Модели отслеживают друг друга тесно в течение симуляции.

Преобразуйте модель Свободного Ответа в `initialCondition` Объект

Скрипт Open Live Script

Получите начальные условия при оценке модели передаточной функции. Преобразуйте initialCondition в модель свободного ответа и модель свободного ответа назад в initialCondition объект.

Загрузите данные и оцените модель sys передаточной функции. Получите предполагаемые начальные условия ic.

load iddata1ic.mat z1i
[sys,ic] = tfest(z1i,2,1);

Преобразуйте ic в idtf модель g свободного ответа.

g = idtf(ic);

Постройте импульсную характеристику g.

impulse(g)
title('Impulse Response of g')

Преобразуйте g назад в initialCondition объект ic1.

ic1 = initialCondition(g);

Постройте импульсную характеристику ic1 путем преобразования ic1 в idss модель.

impulse(idss(ic1))
title('Impulse Response of ic1 in idss form')

Импульсные характеристики кажутся идентичными.

Сравните ic и ic1.

ic.A

ans = 2×2

   -2.9841   -5.5848
    4.0000         0

ic1.A

ans = 2×2

   -2.9841   -5.5848
    4.0000         0

ic.X0

ans = 2×1

   -0.9019
   -0.6161

ic1.X0

ans = 2×1

     4
     0

ic.C

ans = 1×2

    0.2957    5.2441

ic1.C

ans = 1×2

   -0.8745   -1.7215

A матрицы ic и ic1 идентичны. C матрица и X0 вектор отличается. Существует бесконечно много представлений пространства состояний, возможных для данной линейной модели. Два объекта эквивалентны, как проиллюстрировано импульсными характеристиками.

Внешние веб-сайты

Введенный в R2020b

Документация

initialCondition

Описание

Создание

Синтаксис

Описание

Входные параметры

`G` — Модель свободного ответа
Модель LTI

Свойства

`A` — матрица A реализации пространства состояний LTI свободный ответ
числовая матрица

`X0` — Начальные состояния реализации пространства состояний LTI свободный ответ
числовой вектор

`C` — матрица C реализации пространства состояний LTI свободный ответ
числовая матрица

`Ts` Размер шага
0 | –1 | положительная скалярная величина

Функции объекта

Оцените и возвратите начальные условия

Используйте начальные условия

Преобразуйте начальные условия в модель динамической системы

Анализируйте Свободный Ответ Модели с помощью `idss` Форма

Примеры

Получите предполагаемые начальные условия

Визуализируйте свободный ответ на начальное условие

Примените начальные условия в симуляции

Получите начальные условия для новых данных

Получите начальные условия для данных о мультиэксперименте

Создайте `initialCondition` Объект от модели в пространстве состояний

Преобразуйте модель Свободного Ответа в `initialCondition` Объект

Смотрите также

Внешние веб-сайты

Документация System Identification Toolbox

Поддержка

Документация

initialCondition

Описание

Создание

Синтаксис

Описание

Входные параметры

G — Модель свободного ответа Модель LTI

Свойства

A — матрица A реализации пространства состояний LTI свободный ответ числовая матрица

X0 — Начальные состояния реализации пространства состояний LTI свободный ответ числовой вектор

C — матрица C реализации пространства состояний LTI свободный ответ числовая матрица

Ts Размер шага 0 | –1 | положительная скалярная величина

Функции объекта

Оцените и возвратите начальные условия

Используйте начальные условия

Преобразуйте начальные условия в модель динамической системы

Анализируйте Свободный Ответ Модели с помощью idss Форма

Примеры

Получите предполагаемые начальные условия

Визуализируйте свободный ответ на начальное условие

Примените начальные условия в симуляции

Получите начальные условия для новых данных

Получите начальные условия для данных о мультиэксперименте

Создайте initialCondition Объект от модели в пространстве состояний

Преобразуйте модель Свободного Ответа в initialCondition Объект

Смотрите также

Внешние веб-сайты

Документация System Identification Toolbox

Поддержка

`G` — Модель свободного ответа
Модель LTI

`A` — матрица A реализации пространства состояний LTI свободный ответ
числовая матрица

`X0` — Начальные состояния реализации пространства состояний LTI свободный ответ
числовой вектор

`C` — матрица C реализации пространства состояний LTI свободный ответ
числовая матрица

`Ts` Размер шага
0 | –1 | положительная скалярная величина

Анализируйте Свободный Ответ Модели с помощью `idss` Форма

Создайте `initialCondition` Объект от модели в пространстве состояний

Преобразуйте модель Свободного Ответа в `initialCondition` Объект