Об идентифицированных линейных моделях

Что такое Модели IDLTI?

Использование программного обеспечения System Identification Toolbox™ возражает, чтобы представлять множество линейных и нелинейных структур модели. Эти линейные объекты модели коллективно известны как модели Identified Linear Time-Invariant (IDLTI).

Модели IDLTI содержат два отличных динамических компонента:

Измеренный компонент — Описывает отношение между измеренными входными параметрами и измеренным выходом (G)
Шумовой компонент — Описывает отношение между воздействиями при выходе и измеренном выходе (H)

Модели, которые только имеют шумовой H компонента называются timeseries или моделями сигнала. Как правило, вы создаете такие модели с помощью данных timeseries, которые состоят из одних или нескольких выходных параметров y(t) без соответствующего входа.

Общий объем производства является суммой вкладов от измеренных входных параметров и воздействий: y = G u + H e, где u представляет измеренные входные параметры и e воздействие. e(t) моделируется как нулевой средний Гауссов белый шум с отклонением Λ. Следующая фигура иллюстрирует модель IDLTI.

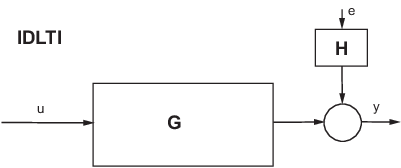
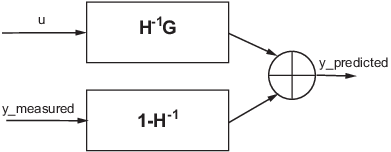
Когда вы симулируете модель IDLTI, вы изучаете эффект входа u(t) (и возможно начальные условия) на выходе y(t). Шумовой e(t) не рассматривается. Однако с предсказанием конечного горизонта выхода, и измеренное и шумовые компоненты модели способствуют расчету (предсказанного) ответа.

Один шаг вперед соответствие модели предсказания линейной идентифицированной модели (y = Gu+He)

Измеренная и шумовая параметризация компонента

Различные линейные структуры модели обеспечивают различные способы параметрировать передаточные функции G и H. Когда вы создаете модель IDLTI или оцениваете модель непосредственно с помощью данных ввода - вывода, можно сконфигурировать структуру и G и H, как описано в следующей таблице:

Тип модели	Передаточные функции G и H	Метод настройки
Модель в пространстве состояний (`idss`)	Представляет идентифицированную структуру модели в пространстве состояний, которой управляют уравнения: $\begin{array}{l} \dot{x} = A x + B u + K e \\ y = C x + D u + e \end{array}$ где передаточная функция между измеренным входом u и выходом y $G (s) = C {(s I - A)}^{- 1} B + D$ и шумовая передаточная функция $H (s) = C {(s I - A)}^{- 1} K + I$ .	Конструкция: используйте `idss` создать модель, задавая значения матриц пространства состояний A, B, C, D и K как входные параметры (использующий `NaNs` обозначить неизвестные записи). Оценка: Использование `ssest` или `n4sid`, задавая пары "имя-значение" для различных настроек, такой как, каноническая параметризация измеренной динамики (`'Form'/'canonical'`), обозначая отсутствие сквозного соединения путем фиксации D, чтобы обнулить (`'Feedthrough'/false`), и отсутствие шумовой динамики путем фиксации K, чтобы обнулить (`'DisturbanceModel'/'none'`).
Полиномиальная модель (`idpoly`)	Представляет полиномиальную модель, такую как ARX, ARMAX и BJ. Модель ARMAX, например, использует уравнение Ay (t) ввода - вывода = Бу (t) +Ce (t), так, чтобы измеренная передаточная функция G была $G (s) = A^{- 1} B$ , в то время как шумовая передаточная функция $H (s) = A^{- 1} C$ . Модель ARMAX является специальной настройкой общей полиномиальной модели, управление которой уравнением: $A y (t) = \frac{B}{F} u (t) + \frac{C}{D} e (t)$ Авторегрессивный компонент, A, распространен между измеренными и шумовыми компонентами. B полиномов и F составляют измеренный компонент, в то время как полиномы C и D составляют шумовой компонент.	Конструкция: Использование `idpoly` создать модель с помощью значений активных полиномов как входные параметры. Например, чтобы создать модель Output-Error, которая использует `G = B/F` как измеренный компонент и имеет тривиальный шумовой компонент (`H = 1`). войдите: y = idpoly([],B,[],[],F) Оценка: используйте `armax`, `arx`, или `bj`, определение порядков полиномов как входные параметры. Например, `bj` требует, чтобы вы задали порядки B, C, D и полиномов F, чтобы создать модель управляющим уравнением $y (t) = \frac{B}{F} u (t) + \frac{C}{D} e (t)$
Модель передаточной функции (`idtf`)	Представляет идентифицированную модель передаточной функции, которая не имеет никаких динамических элементов к шумовому поведению модели. Этот объект использует тривиальную шумовую модель H(s) = I. Управляющее уравнение $y (t) = \frac{n u m}{d e n} u (t) + e (t)$	Конструкция: Использование `idtf` создать модель, задавая значения числителя и коэффициентов знаменателя как входные параметры. Числитель и векторы знаменателя составляют измеренный `G = num(s)/den(s)` компонента. Шумовой компонент фиксируется к `H = 1`. Оценка: Использование `tfest`, определение количества полюсов и нулей измеренного `G` компонента.
Модель процесса (`idproc`)	Представляет модель процесса, которая предоставляет возможности представлять шумовую динамику или как сначала - или как процесс ARMA второго порядка (то есть, H(s)= C(s)/A(s), где C(s) и A(s) являются многочленами равной степени). Измеренный компонент, G(s), представлен передаточной функцией, описанной в нулевой полюсом форме.	Для процесса (и серый ящик) модели, шумовой компонент часто обрабатывается как по требованию расширение в противном случае измеренного компонентно-ориентированного представления. Для этих моделей можно добавить шумовой компонент при помощи `DisturbanceModel` опция оценки. Например: model = procest(data,'P1D') оценивает модель, уравнение которой: $y (s) = K_{p} \frac{1}{(T_{p 1} s + 1)} e^{- s T d} u (s) + e (s) .$ Чтобы добавить компонент шума второго порядка в модель, используйте: Options = procestOptions('DisturbanceModel','ARMA1'); model = procest(data,'P1D',Options); Эта модель имеет уравнение: $y (s) = K_{p} \frac{1}{(T_{p 1} s + 1)} e^{- s T d} u (s) + \frac{1 + c_{1} s}{1 + d_{1} s} e (s)$ где коэффициенты c1 и d1 параметрируют шумовой компонент модели. Если вы создаете модель процесса с помощью `idproc` команда, задайте структуру измеренного компонента с помощью `Type` входной параметр и шумовой компонент при помощи `NoiseTF` пара "имя-значение". Например, model = idproc('P1','Kp',1,'Tp1',1,'NoiseTF',... struct('num',[1 0.1],'den',[1 0.5])) создает модель процесса y(s) = 1/(s+1) u(s) + (s + 0.1)/(s + 0.5) e(s)

Иногда, закрепление коэффициентов или определение границ на параметрах не достаточны. Например, у вас могут быть несвязанные зависимости от параметра в модели, или параметры могут быть функцией различного набора параметров, которые вы хотите идентифицировать исключительно. Например, в системе массового пружинного демпфера, A и B параметры оба зависят от массы системы. Чтобы достигнуть такой параметризации линейных моделей, можно использовать моделирование серого ящика, где вы устанавливаете ссылку между фактическими параметрами и коэффициентами модели путем записывания файла ОДУ. Чтобы узнать больше, смотрите Оценку Модели Серого ящика.

Линейная оценка модели

Вы обычно используете оценку, чтобы создать модели в System Identification Toolbox. Вы выполняете одну из команд оценки, задавая как входные параметры результаты измерений, наряду с другими входными параметрами, необходимыми, чтобы задать структуру модели. Чтобы проиллюстрировать, следующий пример использует команду оценки пространства состояний, ssest, создать модель в пространстве состояний. Первый входной параметр data задает измеренные данные ввода - вывода. Второй входной параметр задает порядок модели.

sys = ssest(data,4)

Функция оценки обрабатывает шумовую переменную e(t) как ошибку предсказания – остаточный фрагмент выхода, который не может быть приписан измеренным входным параметрам. Все алгоритмы оценки работают, чтобы минимизировать взвешенную норму e(t) по промежутку доступных измерений. Функция взвешивания задана природой шумовой передаточной функции H и особое внимание оценки, такой как симуляция или ошибочная минимизация предсказания.

Черный квадрат (“холодный запуск”) оценка

По оценке черного ящика только необходимо задать порядок сконфигурировать структуру модели.

sys = estimator(data,orders)

где estimator имя команды оценки, чтобы использовать для желаемого типа модели.

Например, вы используете tfest оценить модели передаточной функции, arx для моделей полинома структуры ARX, и procest для моделей процессов.

Первый аргумент, data, время - или данные о частотном диапазоне, представленные как iddata или idfrd объект. Второй аргумент, orders, представляет одно или несколько чисел, определения которых зависит от типа модели:

Для передаточных функций, orders относится к количеству полюсов и нулей.
Для моделей в пространстве состояний, orders относится к количеству состояний.
Для моделей процессов, orders обозначает структурные элементы модели процесса, такой как, количество полюсов и присутствие задержки и интегратора.

При работе с приложением вы задаете порядки в соответствующих полях редактирования соответствующих диалоговых окон оценки модели.

Структурированные оценки

В некоторых ситуациях вы хотите сконфигурировать структуру желаемой модели более тесно, чем, что достигается путем простого определения порядков. В таких случаях вы создаете модель шаблона и конфигурируете ее свойства. Вы затем передаете ту модель шаблона как входной параметр к командам оценки вместо orders.

Чтобы проиллюстрировать, следующий пример присваивает значения исходного предположения числителю и полиномам знаменателя модели передаточной функции, налагает минимальные и максимальные границы на их ориентировочные стоимости, и затем передает объект функции средства оценки.

% Initial guess for numerator
num = [1 2];
den = [1 2 1 1];
% Initial guess for the denominator 
sys = idtf(num,den);
% Set min bound on den coefficients to 0.1
sys.Structure.Denominator.Minimum = [1 0.1 0.1 0.1]; 
sysEstimated = tfest(data,sys);

Алгоритм оценки использует обеспеченные исходные предположения, чтобы запустить оценку и поставляет модель, которая уважает заданные границы.

Можно использовать такой шаблон модели, чтобы также сконфигурировать вспомогательные свойства модели, такие как имена ввода/вывода и модули. Если значения некоторых параметров модели первоначально неизвестны, можно использовать NaNs для них в шаблоне.

Опции оценки

Существует много опций, сопоставленных с алгоритмом оценки модели, которые конфигурируют целевую функцию оценки, начальные условия и числовой алгоритм поиска, среди прочего. Для каждой команды оценки, estimator, существует соответствующая команда опции под названием estimatorOptions. Задавать опции для конкретной команды средства оценки, такие как tfest, используйте команду опций, которая соответствует команде оценки, в этом случае, tfestOptions. Команда опций возвращает набор опций, который вы затем передаете как входной параметр соответствующей команде оценки.

Например, чтобы оценить модель полинома структуры Ошибки на выходе, вы используете oe. Задавать simulation как особое внимание и lsqnonlin как метод поиска, вы используете oeOptions:

load iddata1 z1
Options = oeOptions('Focus','simulation','SearchMethod','lsqnonlin');
sys= oe(z1,[2 2 1],Options);

Информация об опциях, используемых, чтобы создать предполагаемую модель, хранится в OptionsUsed поле Report модели свойство. Для получения дополнительной информации см. Отчет Оценки.

Документация