Полюсно-нулевой график динамической системы
pzmap( создание полюсно-нулевого графика модели непрерывной или дискретно-временной динамической системы
sys)sys. x и o обозначает полюса и нули соответственно, как показано на следующем рисунке.
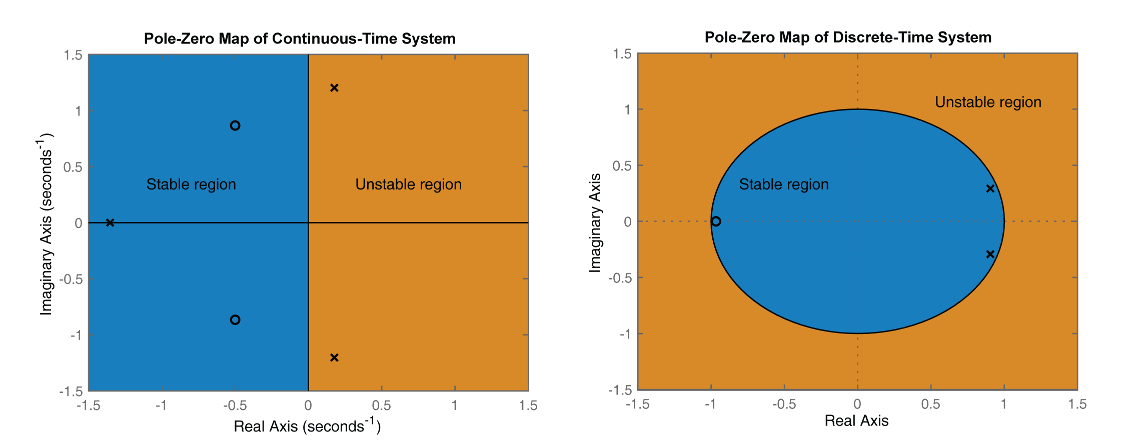
На приведенном выше рисунке линейная инвариантная по времени система с разомкнутым контуром стабильна, если:
В непрерывном режиме все полюса на комплексной s-плоскости должны находиться в левой половине плоскости (синяя область) для обеспечения устойчивости. Система немного устойчива, если отдельные полюса лежат на воображаемой оси, то есть реальные части полюсов равны нулю.
В дискретное время все полюса в комплексной z-плоскости должны лежать внутри единичной окружности (синяя область). Система немного устойчива, если она имеет один или несколько полюсов, лежащих на единичной окружности.
pzmap( создает полюсно-нулевой график нескольких моделей на одной фигуре. Модели могут иметь различное количество входов и выходов и могут представлять собой смесь непрерывных и дискретных систем. Для систем SISO sys1,sys2,...,sysN)pzmap выводит на график системные полюса и нули. Для систем MIMO pzmap строит графики системных полюсов и нулей передачи.
Постройте график полюсов и нулей системы непрерывного времени, представленной следующей передаточной функцией:
1s2 + 3s + 5.
H = tf([2 5 1],[1 3 5]);
pzmap(H)
grid on
При включении сетки отображаются линии постоянного коэффициента демпфирования (дзета) и линии постоянной собственной частоты (wn). Эта система имеет два вещественных нуля, отмеченных на графике o. Система также имеет пару сложных полюсов, отмеченных х.
Постройте график полюсно-нулевой карты дискретного времени идентифицированного состояния-пространства (idss) модель. На практике вы можете получить idss модель по оценке на основе измерений «вход-выход» системы. В этом примере создайте его из данных пространства состояний.
A = [0.1 0; 0.2 -0.9];
B = [.1 ; 0.1];
C = [10 5];
D = [0];
sys = idss(A,B,C,D,'Ts',0.1);Осмотрите карту полюс-ноль.
pzmap(sys)
Системные полюса помечены как x, а нули - как o.
Для этого примера загрузите массив моделей передаточных функций 3 на 1.
load('tfArray.mat','sys'); size(sys)
3x1 array of transfer functions. Each model has 1 outputs and 1 inputs.
Постройте график полюсов и нулей каждой модели в массиве с помощью различных цветов. В этом примере следует использовать красный цвет для первой модели, зеленый цвет для второй и синий цвет для третьей модели в массиве.
pzmap(sys(:,:,1),'r',sys(:,:,2),'g',sys(:,:,3),'b') sgrid
sgrid строит графики постоянного коэффициента демпфирования и собственной частоты в s-плоскости полюсно-нулевого графика.
Использовать pzmap для вычисления полюсов и нулей следующей передаточной функции:
+ 9 .6s + 17
sys = tf([4.2,0.25,-0.004],[1,9.6,17]); [p,z] = pzmap(sys)
p = 2×1
-7.2576
-2.3424
z = 2×1
-0.0726
0.0131
В этом примере используется модель здания с восемью этажами, каждый с тремя степенями свободы: два смещения и один поворот. Отношение ввода-вывода для любого из этих смещений представлено в виде модели с 48 состояниями, где каждое состояние представляет смещение или его скорость изменения (скорость).
Загрузите модель здания.
load('building.mat');
size(G)State-space model with 1 outputs, 1 inputs, and 48 states.
Постройте график полюсов и нулей системы.
pzmap(G)
На графике обратите внимание, что существует множество пар полюс-ноль, которые могут быть потенциально исключены для упрощения модели, без влияния на общую реакцию модели. pzmap полезен для визуальной идентификации таких пар полюс-ноль с близким удалением для выполнения упрощения полюс-ноль.
Использовать функции sgrid или zgrid для построения графика линий постоянного коэффициента демпфирования и собственной частоты в s- или z-плоскости на полюсно-нулевом графике.
Для моделей MIMO pzmap отображает все системные полюса и нули передачи на одном графике. Для отображения полюсов и нулей для отдельных пар ввода-вывода используйте iopzmap.
Дополнительные опции для настройки внешнего вида графика с нулевым полюсом используются pzplot.