Exponenta Banner
exponenta event banner

rlocus

График корневого локуса динамической системы

свернуть все на странице

Синтаксис

rlocus (sys)
rlocus (sys1, sys2,...)
[r, k] = rlocus (sys)
r = rlocus (sys, k)

Описание

пример

rlocus(sys) вычисляет и отображает корневой локус модели SISO sys. Корневой локус возвращает траектории полюсов с замкнутым контуром как функцию коэффициента усиления обратной связи k (предполагая отрицательную обратную связь). Корневые локусы используются для изучения влияния различных коэффициентов усиления обратной связи на положения полюсов с замкнутым контуром. В свою очередь, эти местоположения предоставляют косвенную информацию о временных и частотных откликах.

Вы можете использовать rlocus для построения диаграммы корневого локуса любого из следующих контуров отрицательной обратной связи путем установки sys как показано ниже:

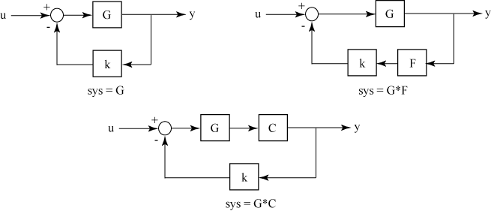
Например, если sys - передаточная функция, представленная

sys (s) = n (s) d (s)

полюса с замкнутым контуром являются корнями

d (s) + kn (s) = 0

График корневого локуса изображает траектории полюсов с замкнутым контуром, когда коэффициент усиления обратной связи k изменяется от 0 до бесконечности. rlocus адаптивно выбирает набор положительных выигрышей k для создания гладкого графика. Полюса на графике локуса корня обозначаются x и нули обозначаются как o.

пример

rlocus(sys1,sys2,...) строит графики корневых локусов нескольких моделей LTI sys1, sys2,... на одном участке. Для каждой модели можно задать цвет, стиль линий и маркер. Дополнительные параметры настройки печати см. в разделе rlocusplot.

пример

[r,k] = rlocus(sys) возвращает вектор коэффициентов усиления обратной связи k и сложные корневые местоположения r за эти выгоды.

пример

r = rlocus(sys,k) использует заданный пользователем вектор коэффициентов усиления обратной связи k для вывода полюсов замкнутого контура r которые определяют график корневого локуса.

Примеры

свернуть все

Открыть сценарий в реальном времени

Для этого примера. постройте график корневого местоположения следующей динамической системы SISO:

sys = 2s2 + 5s + 1s2 + 2s + 3.

sys = tf([2 5 1],[1 2 3]);
rlocus(sys)

Figure contains an axes. The axes contains 4 objects of type line. This object represents sys.

Полюса системы обозначаются x, в то время как нули обозначаются o на графике локуса корня. Для добавления линий сетки, увеличения или уменьшения масштаба, а также для настройки графика можно вызвать редактор свойств.

Для получения дополнительных параметров настройки печати используйте rlocusplot.

Открыть сценарий в реальном времени

В этом примере рассмотрим sisoModels.mat который содержит следующие три модели SISO:

  • sys1 - модель передаточной функции

  • sys2 - модель состояния-пространства

  • sys3 - модель с нулевым усилением полюсов

Загрузить модели из mat файл. 

load('sisoModels.mat','sys1','sys2','sys3');

Создание графика корневого локуса с помощью rlocus и укажите цвет для каждой системы. Также добавьте легенду на график корневого локуса.

rlocus(sys1,'b',sys2,'k',sys3,'r')
hold on
legend('sys1','sys2','sys3')
hold off

Figure contains an axes. The axes contains 13 objects of type line. These objects represent sys1, sys2, sys3.

Рисунок содержит диаграммы корневых локусов для всех трех систем на одном графике. Дополнительные сведения о настройке печати см. в разделе rlocusplot.

Открыть сценарий в реальном времени

В этом примере рассмотрим следующую модель передаточной функции SISO:

sys (s) = 3s2 + 19s3 + 7s2 + 5s + 6

Используйте приведенную выше модель передаточной функции с rlocus для извлечения полюсов с замкнутым контуром и соответствующих значений коэффициента усиления обратной связи.

sys = tf([3 1],[9 7 5 6]);
[r,k] = rlocus(sys)
r = 3×53 complex

  -0.9406 + 0.0000i  -0.8744 + 0.0000i  -0.8685 + 0.0000i  -0.8620 + 0.0000i  -0.8550 + 0.0000i  -0.8475 + 0.0000i  -0.8394 + 0.0000i  -0.8306 + 0.0000i  -0.8212 + 0.0000i  -0.8111 + 0.0000i  -0.8003 + 0.0000i  -0.7888 + 0.0000i  -0.7766 + 0.0000i  -0.7636 + 0.0000i  -0.7500 + 0.0000i  -0.7358 + 0.0000i  -0.7209 + 0.0000i  -0.7055 + 0.0000i  -0.6896 + 0.0000i  -0.6734 + 0.0000i  -0.6569 + 0.0000i  -0.6402 + 0.0000i  -0.6236 + 0.0000i  -0.6071 + 0.0000i  -0.5908 + 0.0000i  -0.5748 + 0.0000i  -0.5593 + 0.0000i  -0.5443 + 0.0000i  -0.5299 + 0.0000i  -0.5161 + 0.0000i  -0.5030 + 0.0000i  -0.4906 + 0.0000i  -0.4789 + 0.0000i  -0.4679 + 0.0000i  -0.4576 + 0.0000i  -0.4480 + 0.0000i  -0.4390 + 0.0000i  -0.4306 + 0.0000i  -0.4229 + 0.0000i  -0.4157 + 0.0000i  -0.4090 + 0.0000i  -0.4029 + 0.0000i  -0.3972 + 0.0000i  -0.3919 + 0.0000i  -0.3871 + 0.0000i  -0.3826 + 0.0000i  -0.3785 + 0.0000i  -0.3748 + 0.0000i  -0.3713 + 0.0000i  -0.3681 + 0.0000i
   0.0814 + 0.8379i   0.0483 + 0.9140i   0.0453 + 0.9212i   0.0421 + 0.9291i   0.0386 + 0.9377i   0.0349 + 0.9470i   0.0308 + 0.9573i   0.0264 + 0.9686i   0.0217 + 0.9809i   0.0167 + 0.9943i   0.0113 + 1.0090i   0.0055 + 1.0251i  -0.0006 + 1.0426i  -0.0071 + 1.0617i  -0.0139 + 1.0826i  -0.0210 + 1.1053i  -0.0284 + 1.1300i  -0.0362 + 1.1568i  -0.0441 + 1.1859i  -0.0522 + 1.2175i  -0.0605 + 1.2515i  -0.0688 + 1.2883i  -0.0771 + 1.3278i  -0.0853 + 1.3703i  -0.0935 + 1.4158i  -0.1015 + 1.4644i  -0.1092 + 1.5162i  -0.1167 + 1.5714i  -0.1239 + 1.6299i  -0.1308 + 1.6920i  -0.1374 + 1.7578i  -0.1436 + 1.8273i  -0.1494 + 1.9006i  -0.1549 + 1.9780i  -0.1601 + 2.0594i  -0.1649 + 2.1452i  -0.1694 + 2.2354i  -0.1736 + 2.3302i  -0.1775 + 2.4299i  -0.1810 + 2.5345i  -0.1844 + 2.6442i  -0.1875 + 2.7594i  -0.1903 + 2.8802i  -0.1929 + 3.0069i  -0.1953 + 3.1397i  -0.1976 + 3.2789i  -0.1996 + 3.4247i  -0.2015 + 3.5775i  -0.2032 + 3.7375i  -0.2048 + 3.9052i
   0.0814 - 0.8379i   0.0483 - 0.9140i   0.0453 - 0.9212i   0.0421 - 0.9291i   0.0386 - 0.9377i   0.0349 - 0.9470i   0.0308 - 0.9573i   0.0264 - 0.9686i   0.0217 - 0.9809i   0.0167 - 0.9943i   0.0113 - 1.0090i   0.0055 - 1.0251i  -0.0006 - 1.0426i  -0.0071 - 1.0617i  -0.0139 - 1.0826i  -0.0210 - 1.1053i  -0.0284 - 1.1300i  -0.0362 - 1.1568i  -0.0441 - 1.1859i  -0.0522 - 1.2175i  -0.0605 - 1.2515i  -0.0688 - 1.2883i  -0.0771 - 1.3278i  -0.0853 - 1.3703i  -0.0935 - 1.4158i  -0.1015 - 1.4644i  -0.1092 - 1.5162i  -0.1167 - 1.5714i  -0.1239 - 1.6299i  -0.1308 - 1.6920i  -0.1374 - 1.7578i  -0.1436 - 1.8273i  -0.1494 - 1.9006i  -0.1549 - 1.9780i  -0.1601 - 2.0594i  -0.1649 - 2.1452i  -0.1694 - 2.2354i  -0.1736 - 2.3302i  -0.1775 - 2.4299i  -0.1810 - 2.5345i  -0.1844 - 2.6442i  -0.1875 - 2.7594i  -0.1903 - 2.8802i  -0.1929 - 3.0069i  -0.1953 - 3.1397i  -0.1976 - 3.2789i  -0.1996 - 3.4247i  -0.2015 - 3.5775i  -0.2032 - 3.7375i  -0.2048 - 3.9052i


k = 1×53
104 ×

         0    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0001    0.0002    0.0002    0.0002    0.0002    0.0002    0.0003    0.0003    0.0003    0.0003    0.0004    0.0004    0.0004    0.0005    0.0005    0.0006    0.0006    0.0007    0.0007    0.0008    0.0009    0.0010    0.0011    0.0012    0.0013    0.0014    0.0015    0.0017    0.0018    0.0020    0.0022    0.0024    0.0026    0.0028    0.0031    0.0034    0.0037    0.0041    0.0045

С тех пор sys содержит 3 полюса, размер результирующего массива полюсов r 3x53. Каждый столбец в r соответствует значению коэффициента усиления от вектора k. Для этого примера: rlocus автоматически выбрал 53 значения k от нуля до бесконечности, чтобы получить гладкую траекторию для трех полюсов с замкнутым контуром. 

display(r(:,39))
  -0.4229 + 0.0000i
  -0.1775 + 2.4299i
  -0.1775 - 2.4299i

display(k(39))
   16.5907

Например, r(:,39) содержит вышеупомянутые полюса замкнутого контура для значения коэффициента усиления обратной связи 16.5907.

Открыть сценарий в реальном времени

В этом примере рассмотрим следующую модель передаточной функции SISO:

sys (s) = 0 .5s2-14s4 + 3s2 + 2

Определите модель передаточной функции и требуемый вектор значений коэффициента усиления обратной связи. Для этого примера рассмотрим набор значений усиления, изменяющихся от 1 до 8 с приращениями 0,5, и извлеките положения полюсов с замкнутым контуром, используя rlocus.

sys = tf([0.5 -1],[4 0 3 0 2]);
k = (1:0.5:5);
r = rlocus(sys,k);
size(r)
ans = 1×2

     4     9

С тех пор sys содержит 4 полюса замкнутого контура, размер результирующего массива местоположений замкнутого полюса r равно 4x9, где 9 столбцов соответствуют 9 конкретным значениям усиления, определенным в k.

Можно также визуализировать траекторию полюсов замкнутого контура для определенных значений коэффициента усиления в k на графике локуса корня. 

rlocus(sys,k)

Figure contains an axes. The axes contains 6 objects of type line. This object represents sys.

Входные аргументы

свернуть все

Динамическая система SISO, заданная как одна из следующих:

  • Непрерывные или дискретные числовые модели LTI, включающие tf, zpk, или ss модели.

  • Обобщенные или неопределенные модели LTI, такие как genss или uss (Надежная панель инструментов управления). (Для использования неопределенных моделей требуется программное обеспечение Toolbox™ надежного управления.)

    rlocus принимает

    • текущие значения перестраиваемых компонентов для перестраиваемых проектных блоков управления.

    • номинальные значения модели для неопределенных проектных блоков управления.

  • Идентифицированные модели LTI, такие как idtf(Панель инструментов идентификации системы), idss(Панель инструментов идентификации системы), idproc(Панель инструментов идентификации системы), idpoly(панель инструментов идентификации системы), и idgrey(Панель инструментов идентификации системы). (Для использования идентифицированных моделей требуется программное обеспечение System Identification Toolbox™.)

Значения коэффициента усиления обратной связи, относящиеся к местоположениям полюсов, заданные как вектор. Коэффициенты усиления обратной связи определяют траекторию полюсов, тем самым влияя на форму графика локуса корня.

Выходные аргументы

свернуть все

Расположение полюсов замкнутого контура sys соответствует каждому значению в k, возвращено как nоколо-m массив, где n - количество полюсов замкнутого контура sys и m = max(length(k)).

Значения коэффициента усиления обратной связи, относящиеся к местоположениям полюсов, возвращаются в виде вектора. Коэффициенты усиления обратной связи определяют траекторию полюсов, тем самым влияя на форму графика локуса корня. Когда k не определен пользователем, rlocus адаптивно выбирает набор положительных выигрышей k между нулем и бесконечностью, чтобы получить гладкий график.

Совет

См. также

| | | | | |

Темы

Представлен до R2006a

Документация по панели инструментов системы управления

Поддержка