Документация

Анализ систем с временными задержками

Можно использовать такие команды анализа, как step, bode, или margin для анализа систем с временными задержками. При выполнении такого анализа программное обеспечение не делает аппроксимаций.

Например, рассмотрим следующий контур управления, в котором установка моделируется как первый порядок плюс время покоя:

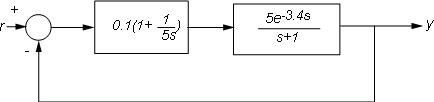
Систему с замкнутым контуром можно моделировать из r кому y со следующими командами:

s = tf('s');
P = 5*exp(-3.4*s)/(s+1);
C = 0.1 * (1 + 1/(5*s));
T = feedback(P*C,1);

T - модель состояния-пространства с внутренней задержкой. Дополнительные сведения о моделях с внутренними задержками см. в разделе Закрытие петель обратной связи с временными задержками.

Постройте график ответа на шаг T:

stepplot(T)

Для более сложных взаимосвязей можно назвать входные и выходные сигналы каждого блока и использовать connect для автоматического контроля за проводкой. Предположим, например, что требуется добавить обратную связь к контуру управления предыдущей модели.

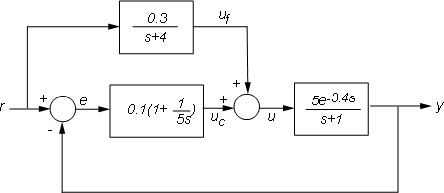
Можно выполнить деривацию соответствующей модели с замкнутым контуром. Tff около

F = 0.3/(s+4);
P.InputName = 'u';  
P.OutputName = 'y';
C.InputName = 'e';  
C.OutputName = 'uc';
F.InputName = 'r';  
F.OutputName = 'uf';
Sum1 = sumblk('e','r','y','+-');    % e = r-y
Sum2 = sumblk('u','uf','uc','++');  % u = uf+uc
Tff = connect(P,C,F,Sum1,Sum2,'r','y');

и сравнить его ответ с конструкцией только обратной связи.

stepplot(T,Tff)
legend('No feedforward','Feedforward')

Представление состояния-пространства отслеживает внутренние задержки в обеих моделях.

s = tf('s');
G = exp(-5*s)/(s+1);
T = feedback(G,.5);
bodemag(T)

G = 1 + 0.5 * exp(-3*s);
bodemag(G)

G = exp(-s) * (0.8*s^2+s+2)/(s^2+s);
T = feedback(G,1);
stepplot(T)

G = 1/(s+1) + exp(-4*s);
T = feedback(1,G);
stepplot(T,150)

Связанные примеры

• Закрытие петель обратной связи с задержками по времени

Подробнее

• Временные задержки в линейных системах
• Внутренние задержки