Адаптивные фильтры представляют собой цифровые фильтры, коэффициенты которых изменяются с целью приведения фильтра в оптимальное состояние. Критерием оптимизации является функция затрат, которая чаще всего является средним квадратом сигнала ошибки между выходом адаптивного фильтра и требуемым сигналом. Когда фильтр адаптирует свои коэффициенты, среднеквадратическая ошибка (MSE) сходится к своему минимальному значению. В этом состоянии фильтр адаптируется, и коэффициенты сходятся к решению. Затем говорят, что выходной сигнал фильтра y (k) очень близко соответствует требуемому сигналу d (k). При изменении характеристик входных данных, иногда называемых средой фильтрации, фильтр адаптируется к новой среде путем создания нового набора коэффициентов для новых данных.
Общий алгоритм адаптивного фильтра
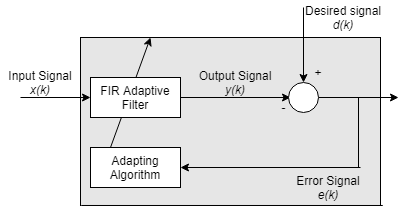
Объект адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптивного фильтра FIR блочной LMS | |
Алгоритм адаптивного фильтра FIR Filtered-x LMS | |
Алгоритм адаптивного фильтра КИХ LMS Нормализованный алгоритм адаптивного фильтра КИХ LMS Алгоритм адаптивного фильтра LMS FIR со знаком-данными Алгоритм адаптивного фильтра LMS FIR со знаком ошибки Алгоритм жестового адаптивного фильтра КИХ LMS |
Блок адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптивного фильтра FIR блочной LMS | |
Алгоритм адаптивного фильтра ПИХ блочного LMS в частотной области | |
Алгоритм адаптивного фильтра КИХ LMS Нормализованный алгоритм адаптивного фильтра КИХ LMS Алгоритм адаптивного фильтра LMS FIR со знаком-данными Алгоритм адаптивного фильтра LMS FIR со знаком ошибки Алгоритм жестового адаптивного фильтра КИХ LMS | |
| Обновление LMS | Алгоритм обновления веса КИО СУО Нормализованный алгоритм обновления веса КИО LMS Алгоритм обновления веса КИХ СКВ со знаком-данными Алгоритм обновления веса КИО LMS со знаком ошибки Алгоритм обновления веса КИО СУО |
Объект адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптации быстрых поперечных наименьших квадратов Алгоритм адаптации FTF скользящего окна | |
QR-декомпозиционный алгоритм адаптации RLS Алгоритм адаптации RLS хозяина Алгоритм адаптации SWRLS домохозяина Алгоритм адаптации рекурсивных наименьших квадратов (RLS) Алгоритм адаптации RLS скользящего окна (ПО) |
Блок адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм экспоненциально взвешенных рекурсивных наименьших квадратов (RLS) |
Объект адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм аффинной проекции, использующий прямую инверсию матрицы Алгоритм аффинной проекции, использующий рекурсивное обновление матрицы Алгоритм адаптации аффинной проекции блока |
Объект адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптации частотной области с ограничениями Алгоритм адаптации без ограничений по частотной области Алгоритм адаптации секционированной и ограниченной частотной области Алгоритм адаптации секционированной и неограниченной частотной области |
Блок адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптации частотной области с ограничениями Алгоритм адаптации без ограничений по частотной области Алгоритм адаптации секционированной и ограниченной частотной области Алгоритм адаптации секционированной и неограниченной частотной области |
Объект адаптивного фильтра | Алгоритм адаптации |
|---|---|
Алгоритм адаптации градиентного адаптивного решетчатого фильтра Алгоритм адаптации решетки наименьших квадратов Алгоритм адаптации RLS декомпозиции QR |
Для получения дополнительной информации об этих алгоритмах см. раздел алгоритмов соответствующих справочных страниц. Полные описания теории появляются в ссылках на адаптивный фильтр [1] и [2].
В установившемся состоянии, когда фильтр адаптирован, погрешность между выходом фильтра и требуемым сигналом минимальна, а не равна нулю. Эта ошибка называется ошибкой устойчивого состояния. Скорость, с которой фильтр сходится к оптимальному состоянию, известному как скорость сходимости, зависит от множества факторов, таких как характер входного сигнала, выбор алгоритма адаптивного фильтра и размер шага алгоритма. Выбор алгоритма фильтра обычно зависит от таких факторов, как производительность сходимости, необходимая для приложения, вычислительная сложность алгоритма, стабильность фильтра в среде и любые другие ограничения.
Алгоритм LMS прост в реализации, но имеет проблемы стабильности. Нормализованная версия алгоритма LMS поставляется с улучшенной скоростью сходимости, большей стабильностью, но имеет повышенную вычислительную сложность. Пример сравнения этих двух параметров см. в разделе Сравнение производительности сходимости между алгоритмом LMS и нормализованным алгоритмом LMS. Алгоритмы RLS очень стабильны, очень хорошо работают в изменяющихся во времени средах, но вычислительно более сложны, чем алгоритмы LMS. Сравнение см. в разделе Сравнение алгоритмов адаптивного фильтра RLS и LMS. Аффинные проекционные фильтры хорошо работают, когда входные данные окрашены и имеют очень хорошие характеристики сходимости. Адаптивные решётчатые фильтры обеспечивают хорошую сходимость, но имеют повышенную вычислительную стоимость. Выбор алгоритма зависит от среды и специфики приложения.
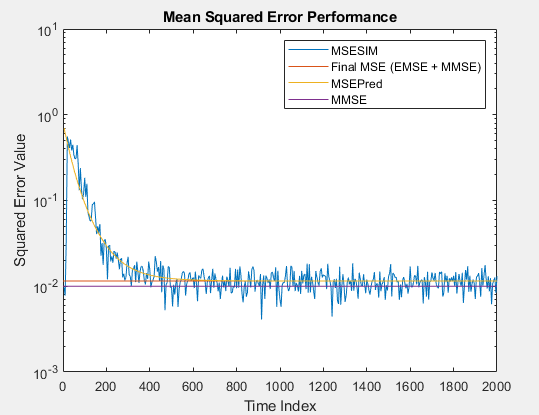
Минимизация среднего квадрата сигнала ошибки между выходом адаптивного фильтра и требуемым сигналом является наиболее распространенным критерием оптимизации для адаптивных фильтров. Фактический MSE (MSESIM) реализуемого адаптивного фильтра может быть определен с помощью msesim функция. Ожидается, что траектория этого MSE будет следовать траектории прогнозируемого MSE (MSEPred), которая вычисляется с использованием msepred функция. Минимальная среднеквадратическая ошибка (MMSE) оценивается по msepred с помощью фильтра Винера. Фильтр Вайнера минимизирует среднеквадратичную ошибку между требуемым сигналом и входным сигналом, отфильтрованным фильтром Винера. Большое значение среднеквадратичной ошибки указывает на то, что адаптивный фильтр не может точно отслеживать требуемый сигнал. Минимальное значение среднеквадратичной ошибки гарантирует оптимальность адаптивного фильтра. Избыточная среднеквадратическая ошибка (EMSE), определяемая msepred функция - это разность между MSE, введенным адаптивными фильтрами, и MMSE, произведенным соответствующим фильтром Винера. Конечный MSE, показанный ниже, является суммой EMSE и MMSE и равен прогнозируемому MSE после сходимости.
Одним из распространенных приложений адаптивного фильтра является использование адаптивных фильтров для идентификации неизвестной системы, такой как отклик неизвестного канала связи или частотный отклик зрительного зала, для выбора довольно расходящихся приложений. Другие приложения включают эхо-подавление и идентификацию канала.
На рисунке неизвестная система размещена параллельно адаптивному фильтру. Этот макет представляет собой только одну из многих возможных структур. Затененная область содержит адаптивную систему фильтров.
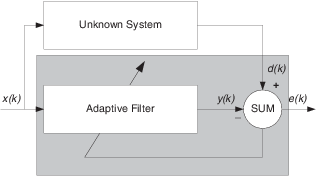
Ясно, что когда e (k) очень мал, отклик адаптивного фильтра близок к отклику неизвестной системы. В этом случае один и тот же вход подает как адаптивный фильтр, так и неизвестный. Если, например, неизвестная система является модемом, вход часто представляет белый шум и является частью звука, который вы слышите от модема при входе в интернет-провайдер.
Размещая неизвестную систему последовательно с адаптивным фильтром, фильтр адаптируется, чтобы стать обратным неизвестной системе, так как e (k) становится очень маленьким. Как показано на чертеже, процесс требует задержки, введенной в желаемый тракт сигнала d (k), чтобы сохранить данные на этапе суммирования синхронизированными. Добавление задержки сохраняет причинно-следственную связь с системой.
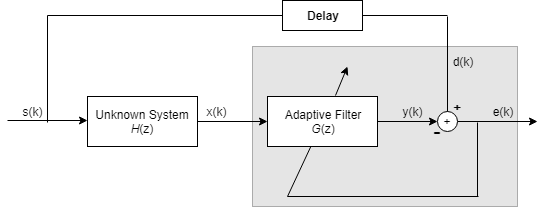
Включение задержки для учета задержки, вызванной неизвестной системой, предотвращает это условие.
Обычные старые телефонные системы (POTS) обычно используют инверсную системную идентификацию для компенсации медной среды передачи. При передаче данных или речи по телефонным линиям медные провода ведут себя как фильтр, имеющий отклик, который скатывается на более высоких частотах (или скоростях передачи данных) и имеющий и другие аномалии.
Добавление адаптивного фильтра, который имеет отклик, обратный отклику провода, и настройка фильтра для адаптации в реальном времени позволяет фильтру компенсировать откат и аномалии, увеличивая доступный диапазон выходной частоты и скорость передачи данных для телефонной системы.
При шумоподавлении адаптивные фильтры позволяют удалять шум из сигнала в реальном времени. Здесь нужный сигнал, который нужно очистить, объединяет шум и требуемую информацию. Чтобы удалить шум, подайте сигнал n '(k) в адаптивный фильтр, который коррелирует с шумом, который должен быть удален из требуемого сигнала .
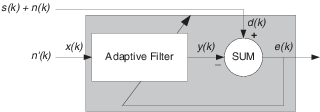
До тех пор, пока входной шум в фильтр остается коррелированным с нежелательным шумом, сопровождающим требуемый сигнал, адаптивный фильтр корректирует свои коэффициенты для уменьшения значения разности между y (k) и d (k), устраняя шум и получая чистый сигнал в e (k). Обратите внимание, что в этом приложении сигнал ошибки фактически сходится к входному сигналу данных, а не сходится к нулю.
Для прогнозирования сигналов необходимо сделать некоторые ключевые предположения. Предположим, что сигнал либо постоянно, либо медленно изменяется во времени, и также периодически во времени.
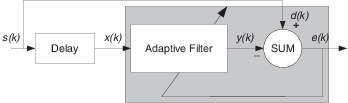
Принимая эти допущения, адаптивный фильтр должен предсказать будущие значения требуемого сигнала на основе прошлых значений. Когда s (k) является периодическим и фильтр достаточно длинный для запоминания предыдущих значений, эта структура с задержкой во входном сигнале может выполнять предсказание. Эту структуру можно использовать для удаления периодического сигнала из стохастических шумовых сигналов.
Наконец, обратите внимание, что большинство систем, представляющих интерес, содержат элементы более чем одной из четырех адаптивных структур фильтров. Для определения того, к чему адаптивный фильтр адаптируется, может потребоваться тщательный анализ реальной структуры.
Кроме того, для ясности на чертежах не отображаются аналого-цифровые (A/D) и цифроаналоговые (D/A) компоненты. Поскольку предполагается, что адаптивные фильтры являются цифровыми по своей природе, и многие проблемы создают аналоговые данные, преобразование входных сигналов в аналоговую область и из нее, вероятно, необходимо.
[1] Хейс, Монсон Х., Статистическая цифровая обработка и моделирование сигналов. Хобокен, Нью-Джерси: John Wiley & Sons, 1996, pp.493-552.
[2] Хайкин, Саймон, теория адаптивных фильтров. Река Верхнее Седло, Нью-Джерси: Прентис-Холл, Инк., 1996.