Выполнение выбора переменных предиктора для байесовских моделей линейной регрессии
Чтобы оценить апостериорное распределение стандартной байесовской модели линейной регрессии, см. estimate.
PosteriorMdl = estimate(PriorMdl,X,y)estimate также осуществляет выбор переменной предиктора.
PriorMdl определяет совместное предварительное распределение параметров, структуру модели линейной регрессии и алгоритм выбора переменной. X является данными предиктора и y - данные ответа. PriorMdl и PosteriorMdl не являются одним и тем же типом объекта.
Произвести PosteriorMdl, estimate обновляет предыдущее распределение информацией о параметрах, которые оно получает из данных.
NaNs в данных указывают отсутствующие значения, которые estimate удаляет, используя удаление по списку.
PosteriorMdl = estimate(PriorMdl,X,y,Name,Value)'Lambda',0.5 указывает, что значение параметра усадки для байесовской регрессии лассо равно 0.5 для всех коэффициентов, за исключением перехвата.
При указании Beta или Sigma2, то PosteriorMdl и PriorMdl равны.
[ использует любую из комбинаций входных аргументов в предыдущих синтаксисах, а также возвращает таблицу, которая включает следующее для каждого параметра: апостериорные оценки, стандартные ошибки, 95% достоверные интервалы и апостериорную вероятность того, что параметр больше 0.PosteriorMdl,Summary] = estimate(___)
Рассмотрим модель множественной линейной регрессии, которая предсказывает реальный валовой национальный продукт США (GNPR) с использованием линейной комбинации индекса промышленного производства (IPI), общая занятость (E) и реальная заработная плата (WR).
β3WRt + αt.
Для всех - это ряд независимых гауссовых возмущений со средним значением 0 и дисперсией .
Предположим, что предыдущие распределения:
Для k = 0..., 3, есть лапласовское распределение со средним из 0 и масштабом , где - параметр сжатия. Коэффициенты условно независимы.
B А В - форма и масштаб, соответственно, обратного гамма-распределения.
Создайте предыдущую модель для байесовской регрессии лассо. Укажите количество предикторов, тип предыдущей модели и имена переменных. Задайте следующие усадки:
0.01 для перехвата
10 для IPI и WR
1e5 для E потому что она имеет масштаб, который на несколько порядков больше, чем другие переменные
Порядок усадок следует за порядком указанных имен переменных, но первым элементом является усадка пересечения.
p = 3; PriorMdl = bayeslm(p,'ModelType','lasso','Lambda',[0.01; 10; 1e5; 10],... 'VarNames',["IPI" "E" "WR"]);
PriorMdl является lassoblm Объект байесовской модели линейной регрессии, представляющий предварительное распределение коэффициентов регрессии и дисперсии возмущений.
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Выполните байесовскую регрессию лассо, передав предыдущую модель и данные в estimate, то есть оценивая апостериорное распределение и . Байесовская регрессия лассо использует марковскую цепь Монте-Карло (MCMC) для выборки из задней. Для воспроизводимости задайте случайное начальное число.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: lasso MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
-------------------------------------------------------------------------
Intercept | -1.3472 6.8160 [-15.169, 11.590] 0.427 Empirical
IPI | 4.4755 0.1646 [ 4.157, 4.799] 1.000 Empirical
E | 0.0001 0.0002 [-0.000, 0.000] 0.796 Empirical
WR | 3.1610 0.3136 [ 2.538, 3.760] 1.000 Empirical
Sigma2 | 60.1452 11.1180 [42.319, 85.085] 1.000 Empirical
PosteriorMdl является empiricalblm объект модели, хранящий черпания из задних распределений и , учитывая данные. estimate отображает сводку краевых задних распределений в командной строке MATLAB ®. Строки сводки соответствуют коэффициентам регрессии и дисперсии возмущений, а столбцы - характеристикам заднего распределения. Характеристики включают в себя:
CI95, который содержит 95% байесовских равных достоверных интервалов для параметров. Например, апостериорная вероятность того, что коэффициент регрессии IPI в [4.157, 4.799] равно 0.95.
Positive, которая содержит апостериорную вероятность того, что параметр больше 0. Например, вероятность того, что перехват больше 0, равна 0.427.
Постройте график задних распределений.
plot(PosteriorMdl)

Учитывая усадку, распределение E довольно плотный около 0. Поэтому E может не быть важным предиктором.
По умолчанию estimate рисует и отбрасывает загоревшую выборку размером 5000. Тем не менее, хорошей практикой является проверка следового графика розыгрышей на предмет адекватного смешивания и отсутствия скороспелости. Постройте график трассировки черчений для каждого параметра. Доступ к чертежам, составляющим распределение (свойства BetaDraws и Sigma2Draws) с использованием точечной нотации.
figure; for j = 1:(p + 1) subplot(2,2,j); plot(PosteriorMdl.BetaDraws(j,:)); title(sprintf('%s',PosteriorMdl.VarNames{j})); end

figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');
Графики следов показывают, что розыгрыши, по-видимому, хорошо смешиваются. Графики не показывают обнаруживаемую переходность или последовательную корреляцию, и розыгрыши не переходят между состояниями.
Рассмотрим регрессионную модель в разделе Выбор переменных с использованием байесовской регрессии лассо.
Создайте предыдущую модель для выбора стохастической переменной поиска (SSVS). Предположим, что и зависимы (модель сопряженной смеси). Укажите количество предикторов p и названия коэффициентов регрессии.
p = 3; PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Реализовать SSVS путем оценки краевых задних распределений и . Поскольку SSVS использует цепь Маркова Monte Carlo для оценки, установите начальное число случайных чисел для воспроизведения результатов.
rng(1); PosteriorMdl = estimate(PriorMdl,X,y);
Method: MCMC sampling with 10000 draws
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution Regime
----------------------------------------------------------------------------------
Intercept | -18.8333 10.1851 [-36.965, 0.716] 0.037 Empirical 0.8806
IPI | 4.4554 0.1543 [ 4.165, 4.764] 1.000 Empirical 0.4545
E | 0.0010 0.0004 [ 0.000, 0.002] 0.997 Empirical 0.0925
WR | 2.4686 0.3615 [ 1.766, 3.197] 1.000 Empirical 0.1734
Sigma2 | 47.7557 8.6551 [33.858, 66.875] 1.000 Empirical NaN
PosteriorMdl является empiricalblm объект модели, хранящий черпания из задних распределений и , учитывая данные. estimate отображает сводку по краевым задним распределениям в командной строке. Строки сводки соответствуют коэффициентам регрессии и дисперсии возмущений, а столбцы - характеристикам заднего распределения. Характеристики включают в себя:
CI95, который содержит 95% байесовских равных достоверных интервалов для параметров. Например, апостериорная вероятность того, что коэффициент регрессии E (стандартизировано) в [0,000, 0,0,002] равно 0,95.
Regime, который содержит предельную заднюю вероятность включения переменной ( 1 для переменной). Например, задняя вероятностьE который должен быть включен в модель 0,0925.
Предполагается, что переменные с Regime < 0.1 следует удалить из модели, результаты показывают, что можно исключить уровень безработицы из модели.
По умолчанию estimate рисует и отбрасывает загоревшую выборку размером 5000. Тем не менее, хорошей практикой является проверка следового графика розыгрышей на предмет адекватного смешивания и отсутствия скороспелости. Постройте график трассировки черчений для каждого параметра. Доступ к чертежам, составляющим распределение (свойства BetaDraws и Sigma2Draws) с использованием точечной нотации.
figure; for j = 1:(p + 1) subplot(2,2,j); plot(PosteriorMdl.BetaDraws(j,:)); title(sprintf('%s',PosteriorMdl.VarNames{j})); end

figure;
plot(PosteriorMdl.Sigma2Draws);
title('Sigma2');
Графики следов показывают, что розыгрыши, по-видимому, хорошо смешиваются. Графики не показывают обнаруживаемую переходность или последовательную корреляцию, и розыгрыши не переходят между состояниями.
Рассмотрим регрессионную модель и предварительное распределение в разделе Выбор переменных с использованием байесовской регрессии лассо.
Создайте предыдущую модель байесовской регрессии лассо для 3 предикторов и укажите имена переменных. Укажите значения усадки 0.01, 10, 1e5, и 10 для перехвата и коэффициентов IPI, E, и WR.
p = 3; PriorMdl = bayeslm(p,'ModelType','lasso','VarNames',["IPI" "E" "WR"],... 'Lambda',[0.01; 10; 1e5; 10]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,"GNPR"};
Оцените условное апостериорное распределение с учетом данных и того, что 10, и верните сводную таблицу оценки, чтобы получить доступ к оценкам.
rng(1); % For reproducibility [Mdl,SummaryBeta] = estimate(PriorMdl,X,y,'Sigma2',10);
Method: lasso MCMC sampling with 10000 draws
Conditional variable: Sigma2 fixed at 10
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------
Intercept | -8.0643 4.1992 [-16.384, 0.018] 0.025 Empirical
IPI | 4.4454 0.0679 [ 4.312, 4.578] 1.000 Empirical
E | 0.0004 0.0002 [ 0.000, 0.001] 0.999 Empirical
WR | 2.9792 0.1672 [ 2.651, 3.305] 1.000 Empirical
Sigma2 | 10 0 [10.000, 10.000] 1.000 Empirical
estimate отображает сводку условного заднего распределения . Ввиду того, что в процессе оценки при 10 фиксируется, выводы о ней тривиальны.
Показ Mdl.
Mdl
Mdl =
lassoblm with properties:
NumPredictors: 3
Intercept: 1
VarNames: {4x1 cell}
Lambda: [4x1 double]
A: 3
B: 1
| Mean Std CI95 Positive Distribution
---------------------------------------------------------------------------
Intercept | 0 100 [-200.000, 200.000] 0.500 Scale mixture
IPI | 0 0.1000 [-0.200, 0.200] 0.500 Scale mixture
E | 0 0.0000 [-0.000, 0.000] 0.500 Scale mixture
WR | 0 0.1000 [-0.200, 0.200] 0.500 Scale mixture
Sigma2 | 0.5000 0.5000 [ 0.138, 1.616] 1.000 IG(3.00, 1)
Поскольку estimate вычисляет условное апостериорное распределение, возвращает входные данные модели PriorMdl, а не условный задний, в первой позиции списка выходных аргументов.
Просмотрите сводную таблицу оценки.
SummaryBeta
SummaryBeta=5×6 table
Mean Std CI95 Positive Distribution Covariances
__________ __________ ________________________ ________ _____________ _______________________________________________________________________
Intercept -8.0643 4.1992 -16.384 0.01837 0.0254 {'Empirical'} 17.633 0.17621 -0.00053724 0.11705 0
IPI 4.4454 0.067949 4.312 4.5783 1 {'Empirical'} 0.17621 0.0046171 -1.4103e-06 -0.0068855 0
E 0.00039896 0.00015673 9.4925e-05 0.00070697 0.9987 {'Empirical'} -0.00053724 -1.4103e-06 2.4564e-08 -1.8168e-05 0
WR 2.9792 0.16716 2.6506 3.3046 1 {'Empirical'} 0.11705 -0.0068855 -1.8168e-05 0.027943 0
Sigma2 10 0 10 10 1 {'Empirical'} 0 0 0 0 0
SummaryBeta содержит условные апостериорные оценки.
Оцените условные апостериорные распределения , учитывая, что - условное апостериорное среднее y (хранится вSummaryBeta.Mean(1:(end – 1))). Возвращает сводную таблицу оценки.
condPostMeanBeta = SummaryBeta.Mean(1:(end - 1));
[~,SummarySigma2] = estimate(PriorMdl,X,y,'Beta',condPostMeanBeta);Method: lasso MCMC sampling with 10000 draws
Conditional variable: Beta fixed at -8.0643 4.4454 0.00039896 2.9792
Number of observations: 62
Number of predictors: 4
| Mean Std CI95 Positive Distribution
------------------------------------------------------------------------
Intercept | -8.0643 0.0000 [-8.064, -8.064] 0.000 Empirical
IPI | 4.4454 0.0000 [ 4.445, 4.445] 1.000 Empirical
E | 0.0004 0.0000 [ 0.000, 0.000] 1.000 Empirical
WR | 2.9792 0.0000 [ 2.979, 2.979] 1.000 Empirical
Sigma2 | 56.8314 10.2921 [39.947, 79.731] 1.000 Empirical
estimate показывает резюме оценки условного следующего распределения , учитывая данные и что condPostMeanBeta. На дисплее выводы по тривиальны.
Рассмотрим регрессионную модель в разделе Выбор переменных с использованием байесовской регрессии лассо.
Создайте предыдущую модель для выполнения SSVS. Предположим, что и зависимы (модель сопряженной смеси). Укажите количество предикторов p и названия коэффициентов регрессии.
p = 3; PriorMdl = mixconjugateblm(p,'VarNames',["IPI" "E" "WR"]);
Загрузите набор данных Нельсона-Плоссера. Создайте переменные для последовательности ответа и предиктора.
load Data_NelsonPlosser X = DataTable{:,PriorMdl.VarNames(2:end)}; y = DataTable{:,'GNPR'};
Реализовать SSVS путем оценки краевых задних распределений и . Поскольку SSVS использует цепь Маркова Monte Carlo для оценки, установите начальное число случайных чисел для воспроизведения результатов. Подавление отображения оценки, но возврат сводной таблицы оценки.
rng(1);
[PosteriorMdl,Summary] = estimate(PriorMdl,X,y,'Display',false);PosteriorMdl является empiricalblm объект модели, хранящий черпания из задних распределений и , учитывая данные. Summary - таблица со столбцами, соответствующими задним характеристикам, и строками, соответствующими коэффициентам (PosteriorMdl.VarNames) и дисперсия возмущений (Sigma2).
Отображение матрицы ковариации расчетного параметра (Covariances) и доля раз, когда алгоритм включает каждый предиктор (Regime).
Covariances = Summary(:,"Covariances")Covariances=5×1 table
Covariances
______________________________________________________________________
Intercept 103.74 1.0486 -0.0031629 0.6791 7.3916
IPI 1.0486 0.023815 -1.3637e-05 -0.030387 0.06611
E -0.0031629 -1.3637e-05 1.3481e-07 -8.8792e-05 -0.00025044
WR 0.6791 -0.030387 -8.8792e-05 0.13066 0.089039
Sigma2 7.3916 0.06611 -0.00025044 0.089039 74.911
Regime = Summary(:,"Regime")Regime=5×1 table
Regime
______
Intercept 0.8806
IPI 0.4545
E 0.0925
WR 0.1734
Sigma2 NaN
Regime содержит предельную заднюю вероятность включения переменной ( 1 для переменной). Например, задняя вероятность того, чтоE должно быть включено в модель 0,0925.
Предполагается, что переменные с Regime < 0.1 следует удалить из модели, результаты показывают, что можно исключить уровень безработицы из модели.
PriorMdl - Байесовская модель линейной регрессии для выбора переменных предиктораmixconjugateblm объект модели | mixsemiconjugateblm объект модели | lassoblm объект моделиБайесовская модель линейной регрессии для выбора переменных предиктора, указанная в этой таблице как объект модели.
| Объект модели | Описание |
|---|---|
mixconjugateblm | Зависимая, Гауссовская гамма инверсии смеси спрягает модель для выбора переменной предсказателя SSVS, возвращенного bayeslm |
mixsemiconjugateblm | Независимая модель Gaussian-mixe-inverse-gamma semaconjugate для выбора переменных предсказателя SSVS, возвращаемая bayeslm |
lassoblm | Модель регрессии байесовского лассо, возвращенная bayeslm |
X - Данные предиктораДанные предиктора для модели множественной линейной регрессии, указанной как numObservationsоколо-PriorMdl.NumPredictors числовая матрица. numObservations - количество наблюдений и должно быть равно длине y.
Типы данных: double
y - Данные ответаДанные ответа для модели множественной линейной регрессии, заданной как числовой вектор с numObservations элементы.
Типы данных: double
Укажите дополнительные пары, разделенные запятыми Name,Value аргументы. Name является именем аргумента и Value - соответствующее значение. Name должен отображаться внутри кавычек. Можно указать несколько аргументов пары имен и значений в любом порядке как Name1,Value1,...,NameN,ValueN.
'Sigma2',2 определяет оценку условного апостериорного распределения коэффициентов регрессии, заданных данными, и что указанная дисперсия возмущения равна 2.'Display' - Флаг для отображения сводки байесовской оценки в командной строкеtrue (по умолчанию) | falseФлаг для отображения сводки байесовской оценки в командной строке, указанной как разделенная запятыми пара, состоящая из 'Display' и значение в этой таблице.
| Стоимость | Описание |
|---|---|
true | estimate печатает информацию оценки и таблицу, суммирующую байесовские оценки, в командной строке. |
false | estimate не печатается в командной строке. |
Оценочная информация включает в себя способ оценки, фиксированные параметры, количество наблюдений и количество предикторов. Сводная таблица содержит оценочные задние средние, стандартные отклонения (квадратный корень задней дисперсии), 95% равных достоверных интервалов, заднюю вероятность того, что параметр больше 0, и описание заднего распределения (если известно). Для моделей, выполняющих SSVS, таблица отображения включает столбец для вероятностей включения переменных.
Если указать либо Beta или Sigma2, то estimate включает в экран спецификацию. Соответствующие задние оценки тривиальны.
Пример: 'Display',false
Типы данных: logical
'Beta' - Значение коэффициентов регрессии для условной оценки апостериорного распределения дисперсии возмущений[]) (по умолчанию) | числовой вектор столбцаЗначение коэффициентов регрессии для оценки условного апостериорного распределения дисперсии возмущений, определяемое как пара, разделенная запятыми, состоящая из 'Beta' и (PriorMdl.Intercept + PriorMdl.NumPredictors) -по-1 числовой вектор .estimate оценивает характеристики δ (start2 |y,X,β = Beta), где y является y, X является X, и Beta - значение 'Beta'. Если PriorMdl.Intercept является true, то Beta(1) соответствует перехвату модели. Все остальные значения соответствуют переменным предиктора, которые составляют столбцы X. Beta не может содержать никаких NaN значения (то есть все коэффициенты должны быть известны).
Невозможно указать Beta и Sigma2 одновременно.
По умолчанию estimate не вычисляет характеристики условного заднегруди, соответствующего
Пример: 'Beta',1:3
Типы данных: double
'Sigma2' - Значение дисперсии возмущений для оценки условного апостериорного распределения коэффициентов регрессии[]) (по умолчанию) | положительный числовой скалярЗначение дисперсии возмущений для оценки условного апостериорного распределения коэффициентов регрессии, определяемое как пара, разделенная запятыми, состоящая из 'Sigma2' и положительный числовой скаляр. estimate оценивает характеристики δ (β |y,X,Sigma2), где y является y, X является X, и Sigma2 - значение 'Sigma2'.
Невозможно указать Sigma2 и Beta одновременно.
По умолчанию estimate не вычисляет характеристики условной задней части β.
Пример: 'Sigma2',1
Типы данных: double
'NumDraws' - Моделирование Монте-Карло скорректировало размер выборки1e5 (по умолчанию) | положительное целое числоМоделирование Монте-Карло скорректировало размер выборки, указанный как пара, разделенная запятыми, состоящая из 'NumDraws' и положительное целое число. estimate фактически розыгрыши BurnIn – NumDraws*Thin образцы. Поэтому estimate базирует оценки NumDraws образцы. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.
Пример: 'NumDraws',1e7
Типы данных: double
'BurnIn' - Количество розыгрышей для удаления из начала образца Монте-Карло5000 (по умолчанию) | неотрицательный скалярКоличество вытягиваний, удаляемых из начала выборки Монте-Карло для уменьшения переходных эффектов, указанное как пара, разделенная запятыми, состоящая из 'BurnIn' и неотрицательный скаляр. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.
Совет
Чтобы определить подходящий размер периода горения, определите степень переходного поведения в выборке Монте-Карло, указав 'BurnIn',0, моделируя несколько тысяч наблюдений с использованием simulate, а затем построение контуров.
Пример: 'BurnIn',0
Типы данных: double
'Thin' - Множитель скорректированного размера выборки Monte Carlo1 (по умолчанию) | положительное целое числоСкорректированный множитель размера выборки Монте-Карло, указанный как пара, разделенная запятыми, состоящая из 'Thin' и положительное целое число.
Фактический размер выборки Монте-Карло составляет BurnIn + NumDraws*Thin. После выгорания, estimate отбрасывает каждый Thin – 1 рисует, а затем сохраняет следующий. Для получения подробной информации о том, как estimate сокращает полную выборку Монте-Карло, см. Алгоритмы.
Совет
Чтобы уменьшить потенциальную большую последовательную корреляцию в выборке Монте-Карло или уменьшить потребление памяти для розыгрышей, хранящихся в PosteriorMdl, укажите большое значение для Thin.
Пример: 'Thin',5
Типы данных: double
'BetaStart' - Начальные значения коэффициентов регрессии для выборки MCMCНачальные значения коэффициентов регрессии для выборки Монте-Карло (MCMC) цепи Маркова, указанной как пара, разделенная запятыми, состоящая из 'BetaStart' и вектор числового столбца с (PriorMdl.Intercept + PriorMdl.NumPredictors) элементы. По умолчанию BetaStart - оценка обычных наименьших квадратов (OLS).
Совет
Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметров. Убедитесь, что решения из каждого прогона сходятся к аналогичным значениям.
Пример: 'BetaStart',[1; 2; 3]
Типы данных: double
'Sigma2Start' - Начальные значения дисперсии возмущений для образца MCMCНачальные значения дисперсии возмущений для выборки MCMC, указанные как пара, разделенная запятыми, состоящая из 'Sigma2Start' и положительный числовой скаляр. По умолчанию Sigma2Start - остаточная среднеквадратическая ошибка ОЛС.
Совет
Хорошей практикой является запуск estimate несколько раз с использованием различных начальных значений параметров. Убедитесь, что решения из каждого прогона сходятся к аналогичным значениям.
Пример: 'Sigma2Start',4
Типы данных: double
PosteriorMdl - Байесовская модель линейной регрессии, хранящая характеристики распределенияmixconjugateblm объект модели | mixsemiconjugateblm объект модели | lassoblm объект модели | empiricalblm объект моделиБайесовская модель линейной регрессии, хранящая характеристики распределения, возвращенные как mixconjugateblm, mixsemiconjugateblm, lassoblm, или empiricalblm объект модели.
Если вы не указываете ни Beta или Sigma2 (их значения: []), то estimate обновляет предыдущую модель с использованием вероятности данных для формирования заднего распределения. PosteriorMdl характеризует заднее распределение и является empiricalblm объект модели. Информация PosteriorMdl хранит или отображает помогает решить, важны ли переменные предиктора.
Если указать либо Beta или Sigma2, то PosteriorMdl равняется PriorMdl (две модели являются одним и тем же объектом, в котором хранятся одинаковые значения свойств). estimate не обновляет предыдущую модель для формирования задней модели. Однако Summary сохраняет условные апостериорные оценки.
Для получения дополнительной информации об отображении PosteriorMdl, см. Summary.
Summary - Резюме байесовских оценокСводка байесовских оценок, возвращенная в виде таблицы. Summary содержит ту же информацию, что и отображение сводки оценки (Display). Строки соответствуют параметрам, а столбцы - этим задним характеристикам:
Mean - Заднее среднее
Std - Заднее стандартное отклонение
CI95 - 95% равный достоверный интервал
Positive - Задняя вероятность того, что параметр больше 0
Distribution - Описание предельного или условного заднего распределения параметра, если оно известно
Covariances - Оценочная ковариационная матрица коэффициентов и дисперсии возмущений
Regime - Переменные вероятности включения для моделей, выполняющих SSVS; низкие вероятности указывают на то, что переменная должна быть исключена из модели
Имена строк - это имена в PriorMdl.VarNames. Имя последней строки: Sigma2.
В качестве альтернативы, пройти PosteriorMdl кому summarize для получения сводки байесовских оценок.
Байесовская модель линейной регрессии рассматривает параметры β и start2 в модели множественной линейной регрессии (MLR) yt = xtβ + αt как случайные величины.
Для времени t = 1,...,T:
yt - наблюдаемый ответ.
xt - вектор строки 1-by- (p + 1) наблюдаемых значений p предикторов. Чтобы разместить пересечение модели, x1t = 1 для всех t.
β - вектор (p + 1) -by-1-столбца коэффициентов регрессии, соответствующих переменным, составляющим столбцы xt.
αt - случайное возмущение со средним значением ноля и Cov (λ) = start2IT × T, в то время, как start- T-by-1 вектор, содержащий все возмущения. Эти допущения подразумевают, что вероятность данных
xtβ, start2).
(yt; xtβ, start2) - гауссова плотность вероятности со средним значением xtβ и дисперсией start2, оцениваемой при yt;.
Перед рассмотрением данных необходимо наложить совместное предварительное предположение о распределении на (β, start2). В байесовском анализе выполняется обновление распределения параметров с использованием информации о параметрах, полученных из вероятности получения данных. Результатом является совместное апостериорное распределение (β, start2) или условное апостериорное распределение параметров.
Моделирование Монте-Карло подвержено изменению. Если estimate использует моделирование Монте-Карло, тогда оценки и выводы могут различаться при вызове estimate многократно при, казалось бы, эквивалентных условиях. Воспроизведение результатов оценки перед вызовом estimate, задайте начальное число случайного числа с помощью rng.
На этом рисунке показано, как estimate уменьшает выборку Монте-Карло, используя значения NumDraws, Thin, и BurnIn.
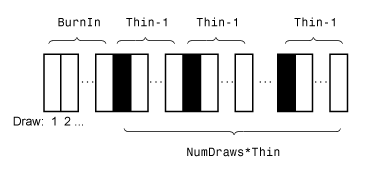
Прямоугольники представляют последовательные розыгрыши из распределения. estimate удаляет белые прямоугольники из образца Монте-Карло. Остающееся NumDraws черные прямоугольники составляют образец Монте-Карло.
Имеется измененная версия этого примера. Открыть этот пример с помощью изменений?
1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.
2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.
3. Сохраняйте структуру оригинального текста - например, не разбивайте одно предложение на два.
4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.
5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.