Измерение свойств областей изображения
stats = regionprops(BW,properties)BW. Вы можете использовать regionprops на смежных областях и несмежных областях (см. Подробнее).
Примечание
Чтобы возвратить измерения 3D объемного изображения, рассмотреть использование regionprops3. В то время как regionprops может принимать 3-D изображения, regionprops3 вычисляет больше статистики для 3-D изображений, чем regionprops.
Для всех синтаксисов, если не указать properties аргумент, затем regionprops возвращает значение 'Area', 'Centroid', и 'BoundingBox' измерения.
stats = regionprops(CC,properties)CC, которая является структурой, возвращенной bwconncomp.
stats = regionprops(L,properties)L.
stats = regionprops(___,I,properties)properties для каждой помеченной области на изображении I. Первый вход в regionprops (BW, CC, или L) определяет регионы в I.
Чтение двоичного изображения в рабочую область.
BW = imread('text.png');Расчет центроидов для связанных компонентов на изображении с помощью regionprops. regionprops функция возвращает центроиды в массиве структуры.
s = regionprops(BW,'centroid');Запишите координаты x и y центроидов в матрицу из двух столбцов.
centroids = cat(1,s.Centroid);
Отображение двоичного изображения с наложенными расположениями центроидов.
imshow(BW) hold on plot(centroids(:,1),centroids(:,2),'b*') hold off
Оцените центр и радиусы круговых объектов на изображении и используйте эту информацию для печати окружностей на изображении. В этом примере: regionprops возвращает свойства измеряемой области в таблице.
Считывание изображения в рабочую область.
a = imread('circlesBrightDark.png');Преобразование входного изображения в двоичное.
bw = a < 100;
imshow(bw)
title('Image with Circles')
Вычислите свойства областей изображения и верните данные в таблицу.
stats = regionprops('table',bw,'Centroid',... 'MajorAxisLength','MinorAxisLength')
stats=4×3 table
Centroid MajorAxisLength MinorAxisLength
________________ _______________ _______________
256.5 256.5 834.46 834.46
300 120 81.759 81.759
330.47 369.83 111.78 110.36
450 240 101.72 101.72
Получить центры и радиусы кругов.
centers = stats.Centroid; diameters = mean([stats.MajorAxisLength stats.MinorAxisLength],2); radii = diameters/2;
Постройте графики кругов.
hold on viscircles(centers,radii); hold off
BW - Двоичное изображениеДвоичный образ, заданный как логический массив любого измерения.
Типы данных: logical
CC - Подключенные компонентыСвязанные компоненты, указанные как структура, возвращаемая bwconncomp.
Типы данных: struct
L - Изображение меткиИзображение метки, указанное как одно из следующих значений.
Числовой массив любого размера. Маркированные пикселы 0 являются фоном. Маркированные пикселы 1 составить один объект; пикселы помечены 2 составляют второй объект; и так далее. regionprops обрабатывает отрицательные пикселы как фон и округляет входные пикселы, не являющиеся целыми числами. Числовое изображение метки можно получить из таких функций маркировки, как watershed или labelmatrix.
Категориальный массив. Каждая категория соответствует другому региону.
Типы данных: single | double | int8 | int16 | int32 | uint8 | uint16 | uint32 | categorical
properties - Тип измерения'basic' (по умолчанию) | разделенный запятыми список строковых скаляров или символьных векторов | массив ячеек строковых скаляров или символьных векторов | 'all'Тип измерения, указанный как разделенный запятыми список строковых скаляров или символьных векторов, массив ячеек строковых скаляров или символьных векторов или как 'all' или 'basic'.
При указании 'all', то regionprops вычисляет все измерения формы и, для изображений в градациях серого, также измерения значения пикселя.
При указании 'basic', то regionprops вычисляет только 'Area', 'Centroid', и 'BoundingBox' измерения.
В следующих таблицах перечислены все свойства, обеспечивающие измерение формы. Свойства, перечисленные в таблице Измерения значения пикселя (Pixel Value Measurements), действительны только при указании изображения в градациях серого.
Измерения формы
| Имя свойства | Описание | Поддержка N-D | Поддержка графического процессора | Создание кода | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
'Area' |
Фактическое количество пикселей в области, возвращаемое как скаляр. (Это значение может немного отличаться от значения, возвращенного Чтобы найти эквивалент площади 3-D тома, используйте | Да | Да | Да | ||||||||
'BoundingBox' | Положение и размер наименьшего поля, содержащего область, возвращаемое в виде 1-по- (2 * Q) вектора. Первые Q-элементы являются координатами минимального угла рамки. Вторые Q-элементы - это размер рамки вдоль каждого размера. Например, ограничительная рамка 2-D со значением | Да | Да | Да | ||||||||
'Centroid' | Центр масс области, возвращенный как 1-by-
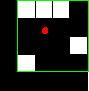
| Да | Да | Да | ||||||||
'Circularity' | Округлость объектов, возвращенная как структура с полем Примечание
| Только 2-D | Нет | Да | ||||||||
'ConvexArea' | Количество пикселей в 'ConvexImage', возвращено как скаляр. | Только 2-D | Нет | Нет | ||||||||
'ConvexHull' | Наименьший выпуклый многоугольник, который может содержать область, возвращаемый в виде матрицы p-by-2. Каждая строка матрицы содержит координаты x и y одной вершины многоугольника. | Только 2-D | Нет | Нет | ||||||||
'ConvexImage' | Изображение, указывающее выпуклый корпус, с заполненными всеми пикселями внутри корпуса (установлено значение on), возвращенный в виде двоичного изображения (logical). Изображение представляет собой размер ограничивающей рамки области. (Для пикселов, через которые проходит граница корпуса, regionprops использует ту же логику, что и roipoly определить, находится ли пиксель внутри или снаружи корпуса.) | Только 2-D | Нет | Нет | ||||||||
'Eccentricity' | Эксцентриситет эллипса, имеющего те же вторые моменты, что и область, возвращен как скаляр. Эксцентриситет - это отношение расстояния между фокусами эллипса и его длиной большой оси. Значение находится в диапазоне от 0 до 1. (0 и 1 - вырожденные случаи. Эллипс, эксцентриситет которого равен 0, фактически является окружностью, в то время как эллипс, эксцентриситет которого равен 1, является отрезком прямой.) | Только 2-D | Да | Да | ||||||||
'EquivDiameter' | Диаметр окружности с той же площадью, что и область, возвращаемый как скаляр. Вычислено как sqrt(4*Area/pi). | Только 2-D | Да | Да | ||||||||
'EulerNumber' | Количество объектов в области минус количество отверстий в этих объектах, возвращаемое как скаляр. Это свойство поддерживается только для матриц меток 2-D. regionprops использует 8-связность для вычисления числа Эйлера (также известного как характеристика Эйлера). Дополнительные сведения о подключении см. в разделе Подключение пикселей. | Только 2-D | Нет | Да | ||||||||
'Extent' | Отношение пикселов в области к пикселям в общей ограничивающей рамке, возвращаемое как скаляр. Вычислено как Area делится на площадь ограничивающей рамки. | Только 2-D | Да | Да | ||||||||
'Extrema' | Экстремальные точки в регионе, возвращенные в виде матрицы 8 на 2. Каждая строка матрицы содержит координаты x и y одной из точек. Формат вектора:
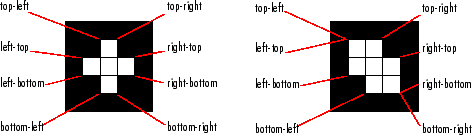
| Только 2-D | Да | Да | ||||||||
'FilledArea' | Количество on пикселы в FilledImage, возвращенный как скаляр. | Да | Нет | Да | ||||||||
'FilledImage' | Изображение того же размера, что и ограничивающая рамка области, возвращаемое как двоичное (
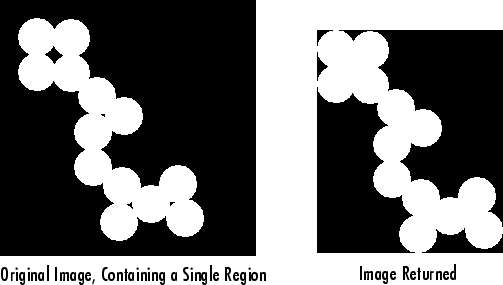
| Да | Нет | Да | ||||||||
'Image' | Изображение того же размера, что и ограничивающая рамка области, возвращаемое как двоичное (logical) массив. on пикселы соответствуют области, а все остальные пикселы off. | Да | Да | Да | ||||||||
'MajorAxisLength' | Длина (в пикселях) большой оси эллипса, имеющей те же нормализованные вторые центральные моменты, что и область, возвращенная в виде скаляра. | Только 2-D | Да | Да | ||||||||
'MaxFeretProperties' | Свойства Feret, включающие максимальный диаметр Feret, его относительный угол и значения координат, возвращаемые в виде структуры с полями:
Вход может представлять собой двоичное изображение, связанный компонент или матрицу меток. | Только 2-D | Нет | Нет | ||||||||
'MinFeretProperties' | Свойства Feret, включающие минимальный диаметр Feret, его относительный угол и значения координат, возвращаемые в виде структуры с полями:
Вход может представлять собой двоичное изображение, связанный компонент или матрицу меток. | Только 2-D | Нет | Нет | ||||||||
'MinorAxisLength' | Длина (в пикселях) малой оси эллипса, имеющей те же нормализованные вторые центральные моменты, что и область, возвращенная в виде скаляра. | Только 2-D | Да | Да | ||||||||
'Orientation' | Угол между осью X и главной осью эллипса с теми же секундными моментами, что и область, возвращается в виде скаляра. Значение в градусах, в диапазоне от -90 градусов до 90 градусов. На этом рисунке показаны оси и ориентация эллипса. В левой части рисунка показана область изображения и соответствующий ей эллипс. На правой стороне показан тот же эллипс с сплошными синими линиями, представляющими оси. Красные точки - это очаги. Ориентация - это угол между горизонтальной пунктирной линией и главной осью.
| Только 2-D | Да | Да | ||||||||
'Perimeter' | Расстояние вокруг границы области возвращено как скаляр.
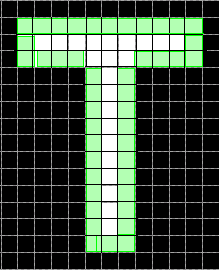
| Только 2-D | Нет | Да | ||||||||
'PixelIdxList' | Линейные индексы пикселей в области, возвращаемые в виде вектора p-элемента. | Да | Да | Да | ||||||||
'PixelList' | Местоположения пикселей в области, возвращаемые как p-by-Q матрица. Каждая строка матрицы имеет вид [x y z ...] и задает координаты одного пикселя в области. | Да | Да | Да | ||||||||
'Solidity' | Доля пикселей в выпуклом корпусе, которые также находятся в области, возвращаемая в виде скаляра. Вычислено как Area/ConvexArea. | Только 2-D | Нет | Нет | ||||||||
'SubarrayIdx' | Элементы L внутри ограничивающей рамки объекта, возвращаемой в виде массива ячеек, который содержит индексы, такие, что L(idx{:}) извлекает элементы. | Да | Да | Нет |
Свойства измерения значения пикселя в следующей таблице действительны только при указании изображения в градациях серого. I.
Измерения значения пикселя
| Имя свойства | Описание | Поддержка N-D | Поддержка графического процессора | Создание кода |
|---|---|---|---|---|
'MaxIntensity' | Значение пикселя с наибольшей интенсивностью в области, возвращаемое как скаляр. | Да | Да | Да |
'MeanIntensity' | Среднее значение всех значений интенсивности в области, возвращаемое как скаляр. | Да | Да | Да |
'MinIntensity' | Значение пикселя с наименьшей интенсивностью в области, возвращаемое как скаляр. | Да | Да | Да |
'PixelValues' | Число пикселей в области, возвращаемое в виде вектора p-by-1, где p - количество пикселей в области. Каждый элемент вектора содержит значение пикселя в области. | Да | Да | Да |
'WeightedCentroid' | Центр области на основе местоположения и значения интенсивности, возвращаемого как p-by-Q вектор координат. Первый элемент WeightedCentroid - горизонтальная координата (или координата x) взвешенного центроида. Второй элемент - это вертикальная координата (или координата y). Все остальные элементы WeightedCentroid в порядке размерности. | Да | Да | Да |
Типы данных: char | string | cell
I - Измеряемое изображениеoutput - Тип возврата'struct' (по умолчанию) | 'table'Возвращаемый тип, указанный как одно из следующих значений.
| Стоимость | Описание |
|---|---|
'struct' | Возвращает массив структур длиной, равной количеству объектов в BW, max(. Поля массива структуры обозначают различные свойства для каждой области, как указано в properties. |
'table' | Возвращает значение |
Типы данных: char | string
ismember полезна для создания двоичного изображения, содержащего только объекты или области, удовлетворяющие определенным критериям. Например, эти команды создают двоичное изображение, содержащее только области, площадь которых больше 80 и эксцентриситет которых меньше 0,8.
cc = bwconncomp(BW); stats = regionprops(cc,'Area','Eccentricity'); idx = find([stats.Area] > 80 & [stats.Eccentricity] < 0.8); BW2 = ismember(labelmatrix(cc),idx);
По умолчанию для 2-D изображений используется соединение 8, а для более высоких размеров - максимальное соединение. Чтобы указать соединение, не используемое по умолчанию, используйте bwconncomp чтобы создать связанные компоненты и затем передать результат в regionprops.
regionprops использует преимущества промежуточных результатов при вычислении соответствующих измерений. Поэтому быстрее всего вычислить все требуемые измерения за один вызов regionprops.
Для большинства измерений требуется мало времени. Однако эти измерения могут занять больше времени в зависимости от количества регионов в L:
'ConvexHull'
'ConvexImage'
'ConvexArea'
'FilledImage'
bwconncomp | bwferet | bwpropfilt | labelmatrix | regionprops3 | watershed