CAGE может решать оптимизацию типа суммы. Эти оптимизации находят оптимальные настройки управляющих параметров в нескольких рабочих точках одновременно. Можно использовать суммарную оптимизацию для решения задач дискового цикла, где необходимо применить ограничения по всему циклу. Например, такое ограничение, как взвешенные выбросы NOx из двигателя < = 3 г/кВт· ч.
При наличии существующей оптимизации точек можно использовать утилиту для создания суммарной оптимизации на основе выходных данных оптимизации точек. Этот подход может помочь найти хорошие начальные значения для оптимизации суммы. Чтобы создать оптимизацию суммы из оптимизации точки, выполните следующие действия.
(Рекомендуется) Выберите «Решение» > «Создать оптимизацию суммы». Дополнительные сведения см. в разделе Создание оптимизации суммы из выходных данных оптимизации точек.
Выберите «Оптимизация» > «Преобразовать в суммарную оптимизацию».
Если оптимизация точек отсутствует, для настройки оптимизации новой суммы выполните следующие действия.
Для создания оптимизации используйте Мастер создания оптимизаций из моделей. В мастере можно настроить цель суммирования. CAGE автоматически правильно настраивает значения переменных для оптимизации суммы, определяя один прогон. Смотрите раздел Что такое бег?.
Можно также настроить цель суммы позже в представлении Оптимизация. См. раздел Изменение цели.
Добавление зависимостей:
В мастере можно добавить ограничение граничной модели.
Чтобы применить другие типы ограничений, необходимо использовать представление Оптимизация (Optimization). Можно применить линейные, эллипсоидные, 1-D таблицы, таблицы 2-D и ограничения диапазона, а некоторые ограничения специфичны для оптимизации суммы - ограничения суммы и ограничения градиента таблицы.
Подробные сведения обо всех этих ограничениях см. в разделе Правка ограничения.
Выберите точки, в которых требуется выполнить оптимизацию:
С помощью мастера можно выбрать подходящие табличные точки останова, наборы данных или модели «точка за точкой» или использовать переменные заданные точки.
Можно также настроить значения переменных оптимизации в представлении Оптимизация (Optimization). Значения можно вводить вручную или путем импорта из наборов данных, таблиц или выходных данных существующих оптимизаций. См. раздел Редактирование переменных значений.
Для оптимизации суммы необходимо иметь один прогон, определяемый элементами управления длиной. CAGE автоматически правильно настраивает значения переменных для оптимизации суммы (определение одного прогона), если:
Используйте утилиту «Создать оптимизацию суммы»
Используйте мастер Создать оптимизацию из модели (Create Optimization from Model), а затем выберите цель суммирования.
При необходимости вместо мастера можно использовать элементы управления длиной в представлении «Оптимизация». См. раздел Выбор скалярных переменных.
(Необязательно) Можно оценить цели или ограничения для различных рабочих точек в соответствии с заданными в оптимизации. См. раздел Использование наборов точек приложения.
Выполните оптимизацию. См. раздел Оптимизация выполнения.
Просмотрите результаты (см. Просмотр результатов оптимизации). Описание выходных данных оптимизации для задач суммирования см. в разделе Интерпретация выходных данных оптимизации суммы.
Оптимизации типа суммы определяют оптимальные настройки рабочих точек одновременно. Таким образом, один вызов алгоритма определяет оптимальные установки параметров управления в каждой рабочей точке.
В CAGE выполнение относится к каждому вызову алгоритма оптимизации.. На панели «Входные значения переменных» указывается количество прогонов, которые должны выполняться CAGE с помощью элемента управления «Количество прогонов». Дополнительные сведения см. в разделе Выбор скалярных переменных.
В следующих разделах описаны элементы управления и выходные данные для оптимизации суммы с использованием следующей задачи примера для иллюстрации.
Скажем, вы создали модели крутящего момента (TQ), остаточной фракции (RESIDFRAC) и температуры выхлопа (EXTEMP) для бензинового двигателя.
Входными данными для этих моделей являются
Опережение искры, S
Синхронизация впускного кулачка, INT
Синхронизация кулачка выпуска, EXH
Частота вращения двигателя, Н
Относительная нагрузка, L
Необходимо настроить оптимизацию для расчета оптимальных настроек S, INT и EXH для следующих рабочих точек:
| N | L |
|---|---|
| 1000 | 0.3 |
| 1100 | 0.2 |
| 1250 | 0.31 |
| 1500 | 0.25 |
| 1625 | 0.18 |
Цель этой оптимизации заключается в следующем:
Максимизируйте взвешенную сумму TQ по рабочим точкам.
Ограничения для этой оптимизации:
Ограничение 1: EXTEMP < = 1290 ° C в каждой рабочей точке
Ограничение 2: RESIDFRAC < = 17% в каждой рабочей точке
Ограничение 3: Изменение в INT составляет не более 5,5 ° на 500 об/мин изменение в N и 5,5 ° на 0,1 изменение в L, оцененное по таблице 3 на 3 (N, L).
Ограничение 4: Изменение в EXH составляет не более 5,5 ° на 500 об/мин изменение в N и 5,5 ° на 0,1 изменение в L, оцененное по таблице 3 на 3 (N, L).
Вы можете использовать fmincon алгоритм в CAGE для решения этой проблемы.
Этот пример используется для пояснения элементов управления и выходных данных в следующих разделах, «Выбор скалярных переменных» и «Интерпретация выходных данных оптимизации суммы».
Дополнительные сведения об ограничениях алгоритма оптимизации в CAGE см. в разделе Ограничения алгоритма.
В узле оптимизации панель Набор точек оптимизации (Optimization Point Set) содержит список свободных и фиксированных переменных. Для оптимизации суммы:
Число рабочих точек - это количество точек, которое оптимизатор суммирует во время оптимизации.
Используйте команду Выбрать скалярные переменные (Select Scalar Variables), чтобы указать скалярные значения, которые не зависят от рабочих точек.
Каждый запуск CAGE Optimization вызывает выбранный алгоритм. Этот алгоритм должен оценивать цели и ограничения (возможно, несколько раз), чтобы позволить ему определить оптимальные настройки свободных переменных. Алгоритмы оптимизации обычно имеют ограничения на количество целевых и ограничительных выходов, которые они могут обрабатывать. В следующей таблице приведены ограничения для двух алгоритмов, представленных в CAGE.
| Имя алгоритма | Цели | Ограничения |
|---|---|---|
| fmincon | Один выход | Любое количество выходов |
| NBI | Два или более выходных данных | Любое количество выходов |
При оценке каждой цели и ограничения во время выполнения количество возвращаемых им выходов зависит от максимального количества значений всех его входов. В следующей таблице приведено количество выходов каждого типа объекта, возвращаемых как функция максимального количества значений всех его входов.
| Тип цели | Максимальное количество значений всех входов в цель | Количество выходов | Причина |
|---|---|---|---|
| Пункт | N | N | Цель точки вычисляется в каждой рабочей точке в рамках прогона, и возвращаются все значения. |
| Сумма | N | Один | Объект sum оценивает модель в каждой рабочей точке и возвращает одно значение, которое является взвешенной суммой оценок модели. |
Аналогично, в следующей таблице подробно описано количество выходов каждого типа ограничения, возвращаемых как функция максимального количества значений всех его входов.
| Тип ограничения | Максимальное количество значений всех входов в ограничение | Количество выходов | Причина |
|---|---|---|---|
| Линейный | N | N | Эти ограничения вычисляются в каждой рабочей точке прогона, и возвращаются все значения. |
| Эллипсоид | N | N | |
| Таблица 1D | N | N | |
| Таблица 2D | N | N | |
| Модель | N | N | |
| Диапазон | N | 0, N или 2N | Ограничение диапазона вычисляет выражение в каждой рабочей точке участка. Ограничение возвращает два значения для каждой точки, расстояние от нижней и верхней границы. В этом случае возвращаются 2N выходные данные. Если одна из границ бесконечна, то для каждой точки возвращается только расстояние до конечной границы, и возвращаются N выходов. Если обе границы бесконечны, то возвращается 0 выходов. |
| Сумма | N | 1 | Ограничение суммы вычисляет модель в каждой рабочей точке и возвращает разницу между взвешенной суммой модели и границей. |
| Стол | N | > = 8 (зависит от настроек) | Зависимость градиента таблицы ограничивает градиент свободной переменной на сетке. Количество возвращаемых выходов зависит от размеров сетки. |
Эти три таблицы можно использовать для проверки того, удовлетворяет ли настроенная задача ограничениям алгоритма. Например, в следующей таблице проверяется, удовлетворяет ли примерная задача (подробно описанная в разделе Пример задачи демонстрации элементов управления для оптимизации суммы) ограничениям алгоритма, выбранного для ее решения. fmincon.
| Цель | Максимальное количество значений всех входов | Количество выходов |
|---|---|---|
| Взвешенная сумма TQ по точкам цикла привода | 5 | 1 (с использованием таблицы Цель (Objective)) |
| Ограничение | Максимальное количество значений всех входов | Количество выходов |
|---|---|---|
| EXTEMP < = 1290 ° C в каждой точке цикла привода | 5 | 5 (с использованием таблицы Ограничение (Constraint)) |
| RESIDFRAC < = 17% в каждой точке цикла привода | 5 | 5 (с использованием таблицы Ограничение (Constraint)) |
| Изменение INT не более 5,5 ° на 500 об/мин и 5,5 ° на 0,1 изменение L | 5 | 24 (это значение является количеством выходных данных ограничений градиента таблицы, сгенерированных из таблицы 3 на 3) |
| Изменение EXH не более 5,5 ° на 500 об/мин и 5,5 ° на 0,1 изменение L | 5 | 24 (это значение является количеством выходных данных ограничений градиента таблицы, сгенерированных из таблицы 3 на 3) |
Таким образом, проблема примера имеет 1 целевой выход и 58 выходных сигналов ограничения. Это удовлетворяет ограничениям fmincon и поэтому алгоритм может быть использован.
Наборы точек приложения можно использовать для оценки ограничений и целей в других рабочих точках, отличных от указанных в оптимизации. Наборы точек приложения можно использовать только с оптимизацией суммы.
Это может быть полезно для некоторых проблем, например:
Проблема калибровки требует учета нескольких циклов привода, определенных в различных наборах рабочих точек. Например, обычно имеют различные циклы привода для производительности и выбросов.
Необходимо применить некоторые ограничения только к подмножеству точек оптимизации (иногда это называется «многорегиональными проблемами»). Например, часто существуют различные ограничения, которые необходимо учитывать при полной нагрузке.
Ваш полный набор интересующих рабочих точек велик, и оптимизация в каждой точке происходит медленно. Можно выполнить оптимизацию в подмножестве точек и вычислить интерполированные результаты в наборе точек приложения.
Возможно, потребуется вычислить двухточечные модели в различных рабочих точках до точек, в которых определены модели.
Чтобы использовать набор точек приложения для оценки цели или ограничения, выполните следующие действия.
Щелкните правой кнопкой мыши цель или ограничение и выберите «Выбрать набор точек приложения».
Откроется диалоговое окно Выбор переменных рабочих точек (Select Operating Point Variables).
Выберите пару переменных для использования в наборах точек приложения. Переменные должны быть фиксированными переменными в оптимизации. Переменные выбираются только один раз для каждой оптимизации. Нажмите кнопку ОК.
Откроется диалоговое окно «Выбор набора точек приложения».
Выберите набор точек приложения. Можно выбрать набор данных или New subset точек оптимизации. Чтобы выбрать подмножество точек, можно использовать флажки или щелкнуть точки на графике.
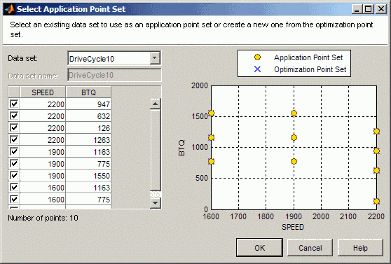
Просмотрите график, отображающий точки приложения и точки оптимизации. CAGE экстраполирует результаты оптимизации для оценки цели или ограничения в точках приложения.
Нажмите кнопку ОК.
Для просмотра примеров графиков, иллюстрирующих использование CAGE наборов точек приложения, введите mbcAppPointSetDemo для загрузки файла примера проекта mbcAppPointSetDemo.cag в CAGE. Выполните оптимизации в проекте для просмотра графиков.