Когда контроллер работает, он использует свое текущее состояние xc в качестве основы для прогнозов. По определению вектор состояния следующий:
xnT (k)].
Здесь,
xc - состояние контроллера, содержащее переменные состояния nxp + nxid + nxod + nxn.
xp - вектор состояния модели растения длиной nxp.
xid - вектор состояния модели входного возмущения длины nxid.
xod - вектор состояния модели выходного возмущения длины nxod.
xn - вектор состояния модели шума измерения длины nxn.
Таким образом, переменные, содержащие xc, представляют модели, представленные на следующей диаграмме системы MPC.
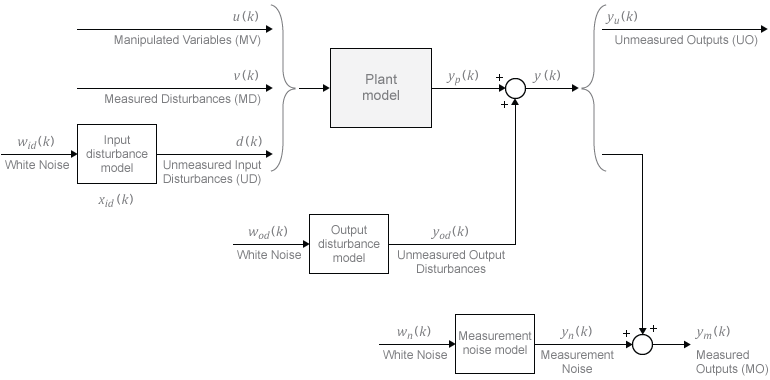
Некоторые векторы состояния могут быть пустыми. Если нет, они появляются в последовательности, определенной в каждой модели.
По умолчанию контроллер автоматически обновляет свое состояние с помощью последних измерений на заводе. Дополнительные сведения см. в разделе Оценка состояния. Кроме того, функция пользовательской оценки состояния позволяет обновлять состояние контроллера с помощью внешней процедуры, а затем передавать эти значения контроллеру. Дополнительные сведения см. в разделе Оценка пользовательского состояния.
Комбинация моделей, показанных на диаграмме, дает наблюдателю состояния:
Cxc (k) + Duo (k).
Контроллер ПДК использует наблюдателя состояния следующими способами:
Оценка значений неизмеренных состояний, необходимых в качестве основы для прогнозирования (см. Оценка состояния).
Чтобы предсказать, как предлагаемые регулятором корректировки регулируемой переменной (СН) повлияют на будущие выходные значения установки (см. Прогноз выходной переменной).
Входными сигналами наблюдателя являются безразмерная установка, управляемая и измеряемая входы возмущений, и входы белого шума для моделей возмущений и шума:
k) wnT (k)].
Выходы наблюдателя - это выходы безразмерной установки.
С точки зрения параметров, определяющих четыре модели, показанные на диаграмме, параметрами наблюдателя являются:
Здесь модели возмущений установки и выходного сигнала переупорядочиваются таким образом, что измеренные выходные сигналы предшествуют неизмеренным выходным сигналам.
В общем случае состояния контроллера не измеряются и должны быть оценены. По умолчанию контроллер использует стационарный фильтр Калмана, получаемый от наблюдателя состояния.
В начале k-го интервала управления состояние контроллера оценивается следующими шагами:
Получите следующие данные:
xc (k 'k-1) - оценка состояния контроллера по предыдущему интервалу управления, k-1
uact (k-1) - Управляемая переменная (MV), фактически используемая в установке от k-1 до k (предполагаемая константа)
uopt (k-1) - оптимальный СН, рекомендованный ПДК и предполагаемый для использования на установке от k-1 до k
v (k) - Измеренные по току возмущения
ym (k) - Текущие измеренные выходы установки
Bu, Bv - столбцы параметра наблюдателя B, соответствующие входам u (k) и v (k)
См - Ряды параметра наблюдателя С, соответствующие измеренным выходам установки
Dmv - Строки и столбцы параметра наблюдателя D, соответствующие измеренным выходам установки и входам измеренных возмущений
L, M - матрицы усиления константы Калмана
Входные и выходные сигналы установки перед использованием в расчетах масштабируются таким образом, чтобы они были безразмерными.
Пересмотрите xc (k 'k-1), когда uact (k-1) и uopt (k-1) различны.
− 1) − uopt (k − 1)]
Вычислите инновации.
) + Dmvv (k)]
Обновление оценки состояния контроллера для учета последних измерений.
1) + Me (k)
Затем программное обеспечение использует текущую оценку состояния xc (k 'k) для решения квадратичной программы на интервале k. Решением является uopt (k), рекомендуемое MPC значение манипулируемой переменной для использования между контрольными интервалами k и k + 1.
Наконец, программное обеспечение готовится к следующему интервалу управления, предполагая, что неизвестные входы, wid (k), wod (k) и wn (k) принимают свое среднее значение (ноль) между временами k и k + 1. Программное обеспечение предсказывает влияние известных входных данных и инноваций следующим образом:
+ Bvv (k) + Le (k)
Программное обеспечение Model Predictive Control Toolbox™ использует kalman команда для вычисления коэффициентов усиления оценщика Калмана L и M. Применяются следующие допущения:
Параметры A, B, C, D наблюдателя состояния являются инвариантными по времени.
Состояния контроллера, xc, являются обнаруживаемыми. (Если нет, или если наблюдатель численно близок к необнаруживаемости, вычисление коэффициента усиления Калмана терпит неудачу, генерируя сообщение об ошибке.)
Стохастические входы wid (k), wod (k) и wn (k) являются независимыми белыми шумами, каждый с нулевым средним и тождественной ковариацией.
Дополнительный белый шум wu (k) и wv (k) с одинаковыми характеристиками добавляет к безразмерным входам u (k) и v (k) соответственно. Это повышает производительность оценщика в определенных случаях, например, когда модель установки является нестабильной с разомкнутым контуром.
Без потери общности установите входы u (k) и v (k) в нуль. Влияние стохастических входов на состояния контроллера и измеряемые выходы установки:
Cmxc (k) + Dmw (k).
Здесь,
k) wnT (k)].
Входные данные для kalman команды представляют собой параметры наблюдателя состояния A, Cm и следующие ковариационные матрицы:
BwwTDmT} = BDmT.
Здесь E {...} обозначает ожидание.
Модельный предиктивный контроль требует прогнозирования безшумных будущих выходов установки, используемых при оптимизации. Это одна из ключевых заявок государственного наблюдателя (см. «Государственный наблюдатель»).
В контрольном интервале k требуемые данные следующие:
p - Горизонт прогнозирования (число контрольных интервалов, которое больше или равно 1)
xc (k 'k) - оценки состояния контроллера (см. Оценка состояния)
v (k) - Токовые измеренные входы возмущений (MD )
v (k + i 'k) - прогнозируемые будущие МД, где i = 1: p-1. Если предварительный просмотр MD не используется, то v (k + i 'k) = v (k).
A, Bu, Bv, C, Dv - константы наблюдателя состояния, где Bu, Bv и Dv обозначают столбцы матриц B и D, соответствующие входам u и v. Du, является нулевой матрицей из-за отсутствия прямого прохождения
Прогнозы предполагают, что неизвестные входные сигналы белого шума равны нулю (их ожидание). Кроме того, прогнозируемые выходы установки должны быть свободны от шума. Таким образом, все термины, включающие в себя состояния шума измерения, исчезают из уравнений наблюдателя состояния. Это эквивалентно обнулению последних элементов nxn xc (k 'k).
Учитывая вышеуказанные данные и упрощения, для первого шага государственный наблюдатель прогнозирует:
| k) + Bvv (k).
Продолжая для последовательных шагов, i = 2: p, наблюдатель состояния прогнозирует:
| k) + Bvv (k + i − 1 | k).
На любом шаге, i = 1: p, прогнозируемые выходы установки без шума:
Dvv (k + i 'k).
Во всех этих уравнениях используются безразмерные входные и выходные переменные установки. См. раздел Определение масштабных коэффициентов. Уравнения также предполагают нулевые смещения. Включение ненулевых смещений является простым.
Для более быстрых вычислений контроллер MPC использует альтернативную форму вышеприведенных уравнений, в которой постоянные члены вычисляются и сохраняются во время инициализации контроллера. См. Матрицы QP.