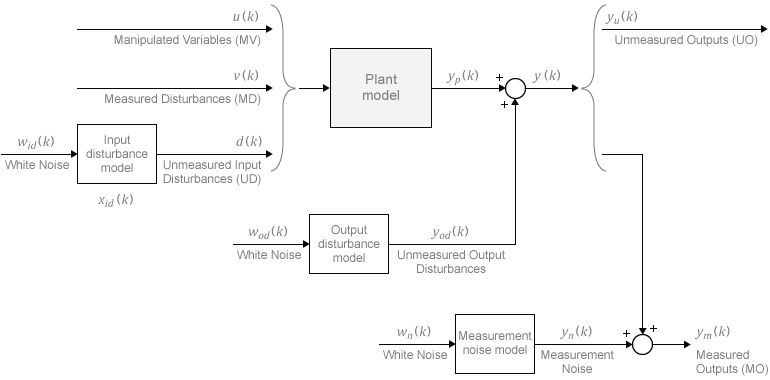
Модельные прогнозирующие контроллеры используют модели растений, возмущений и шума для прогнозирования и оценки состояния. Структура модели, используемая в контроллере MPC, показана на следующей иллюстрации.
Модель завода можно задать в одном из следующих форматов линейного инвариантного времени (LTI):
Числовые модели LTI - Передаточная функция (tf), пространство состояния (ss), нулевой полюс-коэффициент усиления (zpk)
Идентифицированные модели (требуется Toolbox™ идентификации системы) - idss(Панель инструментов идентификации системы), idtf(Панель инструментов идентификации системы), idproc(панель инструментов идентификации системы), и idpoly(Панель инструментов идентификации системы)
Контроллер MPC выполняет все вычисления оценки и оптимизации, используя систему дискретного времени, без задержки, с безразмерными входными и выходными переменными. Поэтому при указании модели завода в контроллере MPC программное обеспечение при необходимости выполняет следующее:
Преобразование в пространство состояний - ss преобразует предоставленную модель в модель состояния-пространства LTI.
Дискретизация или повторная выборка - если время выборки модели отличается от времени выборки контроллера MPC (определено в Ts ), происходит одно из следующих действий:
Если модель является непрерывной, c2d команда преобразует его в дискретный объект LTI с использованием времени выборки контроллера.
Если модель имеет дискретное время, d2d команда производит его повторную выборку для формирования дискретного объекта LTI с использованием времени выборки контроллера.
Удаление задержки - если модель дискретного времени включает какие-либо входные, выходные или внутренние задержки, absorbDelay команда заменяет их соответствующим числом полюсов при z = 0, увеличивая общее число дискретных состояний. InputDelay, OutputDelay, и InternalDelay все свойства результирующей модели состояния-пространства равны нулю.
Преобразование в безразмерные входные и выходные переменные - контроллер MPC позволяет задать масштабный коэффициент для каждой входной и выходной переменной установки. Если масштабные коэффициенты не заданы, они по умолчанию 1. Программное обеспечение преобразует входные и выходные переменные установки в безразмерную форму следующим образом:
k) + So − 1DSiup (k).
где Ap, B, C и D - постоянные матрицы с нулевым запаздыванием и пространством, полученные на этапе 3, и:
Si - диагональная матрица входных масштабных коэффициентов в инженерных единицах.
Как и диагональная матрица выходных масштабных коэффициентов в инженерных единицах.
xp - вектор состояния с шага 3 в инженерных единицах (включая любые состояния поглощенной задержки). Масштабирование переменных состояния не выполняется.
up - вектор безразмерных входных переменных растения, включая управляемые переменные, измеренные возмущения и неизмеренные входные возмущения.
yp - вектор безразмерных выходных переменных растения.
Полученная модель растения имеет следующую эквивалентную форму:
Dpuu (k) + Dpvv (k) + Dpdd (k).
Здесь − 1C, Bpu, Bpv и Bpd являются соответствующими столбцами BSi. Также Dpu, Dpv и Dpd являются соответствующими столбцами − 1DSi. Наконец, u (k), v (k) и d (k) являются безразмерными управляемыми переменными, измеренными возмущениями и неизмеренными входными возмущениями соответственно.
Контроллер MPC обеспечивает ограничение Dpu = 0, что означает, что контроллер не разрешает прямой проход от любой управляемой переменной к любому выходному сигналу установки.
Если модель установки включает неизмеренные входные возмущения d (k), модель входных возмущений определяет тип сигнала и характеристики d (k). Дополнительные сведения о модели см. в разделе Оценка состояния контроллера.
getindist обеспечивает доступ к используемой модели.
Модель входных возмущений является ключевым фактором, влияющим на следующие атрибуты производительности контроллера:
Динамическая реакция на видимые возмущения - характер реакции контроллера, когда измеренный выход установки отклоняется от прогнозируемой траектории вследствие неизвестного возмущения или ошибки моделирования.
Асимптотический отказ от устойчивых возмущений - если модель возмущений предсказывает устойчивое возмущение, регулировки контроллера продолжаются до тех пор, пока выход установки не вернется на желаемую траекторию, эмулируя классический интегральный контроллер обратной связи.
Можно предоставить входную модель возмущения как состояние-пространство LTI (ss), передаточная функция (tf) или с нулевым усилением полюсов (zpk) объект с использованием setindist. Контроллер MPC преобразует входную модель возмущений в дискретную, свободную от задержек, систему состояний-пространства LTI, используя те же шаги, которые используются для преобразования модели установки. Результат:
(k) + Didwid (k).
где Aid, Bid, Cid и Did - матрицы с постоянным пространством состояний, и:
xid (k) - вектор состояний входной модели возмущения nxid ≥ 0.
dk (k) - вектор безразмерных неизмеренных входных возмущений.
wid (k) - вектор nid ≥ 1 безразмерных входных сигналов белого шума, предполагаемый имеющим нулевое среднее значение и единичную дисперсию.
Если модель входного возмущения не предоставляется, то контроллер использует модель по умолчанию, в которой к его выходам добавляются интеграторы с безразмерным единичным усилением. Интегратор добавляется для каждого неизмеренного входного нарушения, если это не приведет к нарушению наблюдаемости состояния. В этом случае вместо него используется статическая система с безразмерным единичным усилением.
Модель выходного возмущения является частным случаем более общей модели входного возмущения. Его выход, yod (k), непосредственно добавляется к выходу установки, а не влияет на состояния установки. Модель выходного возмущения определяет тип сигнала и характеристики yod (k), и она часто используется на практике. Дополнительные сведения о модели см. в разделе Оценка состояния контроллера.
getoutdist обеспечивает доступ к используемой модели выходного возмущения.
В качестве состояния-пространства LTI можно указать пользовательскую модель нарушения выходного сигнала (ss), передаточная функция (tf) или с нулевым усилением полюсов (zpk) объект с использованием setoutdist. Используя те же шаги, что и для модели установки, контроллер MPC преобразует указанную модель выходного возмущения в дискретно-временную, свободную от задержек, систему состояния-пространства LTI. Результат:
(k) + Dodwod (k).
где Aod, Bod, Cod и Dod являются матрицами постоянного состояния-пространства, и:
xod (k) - вектор состояний модели выходного возмущения nxod ≥ 1.
yod (k) - вектор безразмерных выходных возмущений, добавляемый к безразмерным выходным сигналам установки.
wod (k) - вектор безразмерных входных сигналов белого шума, предполагаемый имеющим нулевое среднее и единичную дисперсию.
Если модель выходного возмущения не задана, то контроллер использует модель по умолчанию, в которой к некоторым или всем выходам добавляются интеграторы с безразмерным единичным усилением. Эти интеграторы добавляются в соответствии со следующими правилами:
Для неизмеренных выходов установки никакие нарушения не оцениваются, т.е. интеграторы не добавляются.
Для каждого измеренного выходного сигнала добавляют интегратор в порядке уменьшения выходного веса.
Для изменяющихся во времени весов сумма абсолютных значений во времени рассматривается для каждого выходного канала.
Для равных выходных весов следует порядок в пределах выходного вектора.
Для каждого измеренного выходного сигнала интегратор не добавляется, если это приведет к нарушению наблюдаемости состояния. Вместо этого используется коэффициент усиления со значением, равным нулю.
При наличии входной модели возмущения контроллер добавляет к этой модели интеграторы по умолчанию перед построением модели выходного возмущения по умолчанию.
Одна из целей конструкции контроллера состоит в том, чтобы отличать возмущения, которые требуют реакции, от шума измерения, который следует игнорировать. Модель шума измерения определяет ожидаемый тип и характеристики шума. Дополнительные сведения о модели см. в разделе Оценка состояния контроллера.
Используя те же шаги, что и для модели установки, контроллер MPC преобразует модель измеренного шума в дискретную, свободную от задержек, систему состояния-пространства LTI. Результат:
Cnxn (k) + Dnwn (k).
Здесь An, Bn, Cn и Dn являются матрицами пространства постоянного состояния, и:
xn (k) - вектор состояний шумовой модели nxn ≥ 0.
yn (k) является вектором nym безразмерных шумовых сигналов, добавляемых к безразмерным измеренным выходам установки.
wn (k) - вектор nn ≥ 1 безразмерных входных сигналов белого шума, предполагаемый имеющим нулевое среднее значение и единичную дисперсию.
Если модель шума не задана, по умолчанию используется статическое усиление единицы: nxn = 0, Dn - единичная единичная матрица, а An, Bn и Cn пусты.
Для mpc объект контроллера, MPCobj, собственность MPCobj.Model.Noise обеспечивает доступ к измерительной модели шума.
Примечание
Если минимальное собственное значение меньше 1x10-8, контроллер MPC добавляет 1x10-4 к каждому диагональному элементу Dn. Эта корректировка делает более вероятным успешное вычисление коэффициента усиления Калмана по умолчанию.