Автоматическая дифференциация (также известная как autodiff, AD или алгоритмическая дифференциация) - широко используемый инструмент в оптимизации. solve функция использует автоматическое дифференцирование по умолчанию в проблемной оптимизации для общих нелинейных объективных функций и ограничений; см. раздел Автоматическое дифференцирование в панели инструментов оптимизации.
Автоматическое дифференцирование - это набор методик численной оценки производных (градиентов). Метод использует символические правила дифференцирования, которые точнее конечных аппроксимаций разностей. В отличие от чисто символического подхода, автоматическое дифференцирование вычисляет выражения численно на ранних этапах вычислений, а не выполняет большие символьные вычисления. Другими словами, автоматическая дифференциация оценивает производные при определенных числовых значениях; он не создает символические выражения для производных.
Автоматическое дифференцирование прямого режима вычисляет числовую производную, выполняя операции с элементарной производной одновременно с операциями оценки самой функции. Как подробно описано в следующем разделе, программное обеспечение выполняет эти вычисления на вычислительном графике.
Автоматическое дифференцирование обратного режима использует расширение вычислительного графа прямого режима, чтобы разрешить вычисление градиента посредством обратного прохождения графа. Когда программное обеспечение запускает код для вычисления функции и ее производной, оно записывает операции в структуру данных, называемую трассировкой.
Как отметили многие исследователи (например, Байдин, Перлмуттер, Радул и Сискинд [1]), для скалярной функции многих переменных обратный режим вычисляет градиент более эффективно, чем прямой режим. Поскольку целевая функция является скалярной, solve автоматическое дифференцирование использует обратный режим для скалярной оптимизации. Однако для векторных функций, таких как нелинейные наименьшие квадраты и решение уравнений, solve использует прямой режим для некоторых вычислений. См. раздел Автоматическое дифференцирование в панели инструментов оптимизации.
Рассмотрим проблему оценки этой функции и её градиента:
+ x22)).
Автоматическая дифференциация работает в определенных точках. В этом случае возьмем x1 = 2, x2 = 1/2.
Следующий вычислительный граф кодирует вычисление функции f (x).
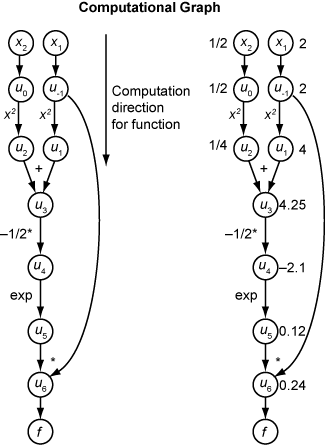
Чтобы вычислить градиент f (x) с помощью прямого режима, вычислите тот же график в том же направлении, но измените вычисление на основе элементарных правил дифференциации. Для дальнейшего упрощения вычисления необходимо заполнить значение производной каждого подэкспрессии. Чтобы вычислить весь градиент, нужно пройти график дважды, один раз для частной производной относительно каждой независимой переменной. Каждое вложенное выражение в правиле цепочки имеет числовое значение, поэтому всё выражение имеет тот же тип графа вычисления, что и сама функция.
Вычисление представляет собой повторное применение правила цепочки. В этом примере производная f относительно x1 расширяется до этого выражения:
Пусть представляет производную выражения ui относительно x1. Используя вычисленные значения ui из вычисления функции, вычисляется частная производная f относительно x1, как показано на следующем рисунке. Обратите внимание, что все значения становятся доступными при прохождении графика сверху вниз.
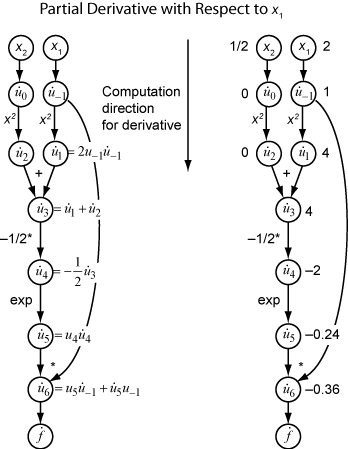
Чтобы вычислить частную производную относительно x2, нужно пройти аналогичный вычислительный график. Поэтому при вычислении градиента функции число проходов по графам совпадает с числом переменных. Этот процесс может быть медленным для многих приложений, когда целевая функция или нелинейные ограничения зависят от многих переменных.
Обратный режим использует одно прямое прохождение вычислительного графа для настройки трассировки. Затем вычисляет весь градиент функции в одном прохождении графа в противоположном направлении. Для проблем со многими переменными этот режим намного эффективнее.
Теория, лежащая в основе обратного режима, также основана на цепном правиле вместе со связанными смежными переменными, обозначаемыми overbar. Смежная переменная для ui
В терминах вычислительного графа каждая исходящая стрелка из переменной вносит вклад в соответствующую смежную переменную по её члену в правиле цепочки. Например, переменная u-1 имеет исходящие стрелки для двух переменных, u1 и u6. Граф имеет связанное уравнение
В этом вычислении, напоминая, что − 12 и u6 = u5u-1, вы получаете
1 + u pu6u5.
Во время прямого прохождения графика программное обеспечение вычисляет промежуточные переменные ui. Во время обратного обхода, начиная с начального значения , вычисление обратного режима получает смежные значения для всех переменных. Следовательно, обратный режим вычисляет градиент только за одно вычисление, экономя много времени по сравнению с прямым режимом.
На следующем рисунке показано вычисление градиента в обратном режиме для функции
+ x22)).
Опять же, вычисление занимает x1 = 2, x2 = 1/2. Вычисление обратного режима основано на значениях ui, которые получаются во время вычисления функции на исходном вычислительном графике. В правой части рисунка вычисленные значения смежных переменных появляются рядом с именами смежных переменных, используя формулы из левой части рисунка.
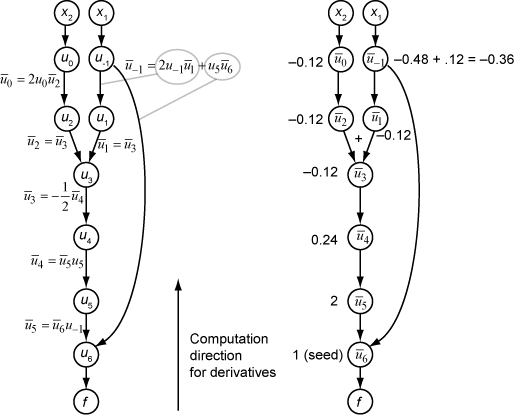
Конечные значения градиента отображаются как и .
Для получения более подробной информации см. Baydin, Pearlmutter, Radul и Siskind [1] или статью Википедии об автоматической дифференциации [2].
Автоматическое дифференцирование (AD) применяется к solve и prob2struct функционирует при следующих условиях:
Поддерживаются функции цели и ограничения, как описано в разделе Поддерживаемые операции с переменными и выражениями оптимизации. Они не требуют использования fcn2optimexpr функция.
Решатель, вызываемый solve является fmincon, fminunc, fsolve, или lsqnonlin.
Для задач оптимизации, 'ObjectiveDerivative' и 'ConstraintDerivative' аргументы пары имя-значение для solve или prob2struct имеют значение 'auto', 'auto-forward', или 'auto-reverse'.
Для задач уравнений, 'EquationDerivative' параметр имеет значение 'auto', 'auto-forward', или 'auto-reverse'.
| Когда применяется AD | Все поддерживаемые функции ограничения | Одно или несколько ограничений не поддерживаются |
|---|---|---|
| Целевая функция поддерживается | AD используется для целей и ограничений | AD используется только для цели |
| Целевая функция не поддерживается | AD используется только для ограничений | AD не используется |
Когда эти условия не выполняются, solve оценивает градиенты по конечным разностям, и prob2struct не создает градиенты в созданных файлах функций.
Решатели по умолчанию выбирают следующий тип AD:
Для общей нелинейной целевой функции fmincon по умолчанию для целевой функции используется обратный AD. fmincon По умолчанию для функции нелинейных ограничений используется обратная AD, если число нелинейных ограничений меньше числа переменных. В противном случае fmincon по умолчанию пересылает AD для функции нелинейных ограничений.
Для общей нелинейной целевой функции fminunc по умолчанию используется обратный AD.
Для целевой функции наименьших квадратов fmincon и fminunc по умолчанию пересылать AD для целевой функции. Определение целевой функции наименьших квадратов на основе задачи см. в разделе Запись целевой функции для наименьших квадратов на основе задачи.
lsqnonlin по умолчанию пересылается AD, если число элементов в целевом векторе больше или равно числу переменных. В противном случае lsqnonlin по умолчанию используется обратный AD.
fsolve по умолчанию пересылается AD, если число уравнений больше или равно числу переменных. В противном случае fsolve по умолчанию используется обратный AD.
Примечание
Использование автоматических производных в проблеме, преобразованной prob2struct, передайте параметры, определяющие эти производные.
options = optimoptions('fmincon','SpecifyObjectiveGradient',true,... 'SpecifyConstraintGradient',true); problem.options = options;
В настоящее время AD работает только для первых производных; он не относится ко вторым или более высоким производным. Так, например, если вы хотите использовать аналитический гессен для ускорения оптимизации, вы не можете использовать solve непосредственно и должен использовать подход, описанный в разделе Дериваты поставки в потоке операций на основе проблем.
[1] Байдин, Атилим Гюнес, Барак А. Перлмуттер, Алексей Андреевич Радул, Джеффри Марк Сискинд. «Автоматическая дифференциация в машинном обучении: опрос». Журнал исследований машинного обучения, 18 (153), 2018, стр. 1-43. Доступно по адресу https://arxiv.org/abs/1502.05767.
[2] Автоматическое дифференцирование. Википедия. Доступно по адресу https://en.wikipedia.org/wiki/Automatic_differentiation.