coneprog

Программный решатель второго порядка

свернуть все на странице

Синтаксис

x = coneprog (f, socConstraints)

x = coneprog (f, socConstraints, A, b, Aeq, beq)

x = coneprog (f, socConstraints, A, b, Aeq, beq, lb, ub)

x = coneprog (f, socConstraints, A, b, Aeq, beq, lb, ub, options)

x = coneprog (проблема)

[x, fval] = coneprog (___)

[x, fval, exitflag, output] = coneprog (___)

[x, fval, exitflag, output, lambda] = coneprog (___)

Описание

coneprog функция - это решатель программирования конуса второго порядка, который находит минимум задачи, указанный в

$\underset{}{}^{} minxfTx$

с учетом ограничений

$\begin{matrix} ‖_{} Asc (i)_{} \cdotx-bsc (i_{)}^{‖} \leqdscT (i) \\ ⋅x−γ \\ (i) \end{matrix}$ A⋅x≤bAeq⋅x=beqlb≤x≤ub.

f, x, b, beq, lb и ub - векторы, а A и Aeq - матрицы. Для каждого i матрица Asc (i), векторы _dsc (i) и _bsc (i) и скаляр γ (i) находятся в ограничении конуса второго порядка, которое создается с помощьюsecondordercone.

Дополнительные сведения об ограничениях конуса см. в разделе Ограничение конуса второго порядка.

пример

x = coneprog(f,socConstraints) решает проблему программирования конуса второго порядка с ограничениями в socConstraints закодировано как

Asc (i) =socConstraints.A(i)
bsc (i) =socConstraints.b(i)
dsc (i) =socConstraints.d(i)
γ (i) =socConstraints.gamma(i)

пример

x = coneprog(f,socConstraints,A,b,Aeq,beq) решает проблему, связанную с ограничениями неравенства A*x ≤ b и ограничения равенства Aeq*x = beq. Набор A = [] и b = [] если неравенства не существует.

пример

x = coneprog(f,socConstraints,A,b,Aeq,beq,lb,ub) определяет набор нижних и верхних границ для конструктивных переменных, x чтобы решение всегда находилось в диапазоне lb ≤ x ≤ ub. Набор Aeq = [] и beq = [] если равенства отсутствуют.

пример

x = coneprog(f,socConstraints,A,b,Aeq,beq,lb,ub,options) минимизирует использование опций оптимизации, указанных в options. Использовать optimoptions для установки этих параметров.

пример

x = coneprog(problem) находит минимальное значение для problem, структура, описанная в problem.

пример

[x,fval] = coneprog(___) также возвращает значение целевой функции в решении fval = f'*x, используя любую из комбинаций входных аргументов в предыдущих синтаксисах.

пример

[x,fval,exitflag,output] = coneprog(___) дополнительно возвращает значение exitflag который описывает условие выхода и структуру output содержит информацию о процессе оптимизации.

пример

[x,fval,exitflag,output,lambda] = coneprog(___) дополнительно возвращает структуру lambda поля которого содержат двойные переменные в решении x.

Примеры

свернуть все

Зависимость «Один конус»

Открыть сценарий в реальном времени

Чтобы настроить проблему с ограничением конуса второго порядка, создайте объект ограничения конуса второго порядка.

A = diag([1,1/2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = 0;
socConstraints = secondordercone(A,b,d,gamma);

Создайте вектор целевой функции.

f = [-1,-2,0];

Проблема не имеет линейных ограничений. Создайте пустые матрицы для этих ограничений.

Aineq = [];
bineq = [];
Aeq = [];
beq = [];

Установить верхние и нижние границы на x(3).

lb = [-Inf,-Inf,0];
ub = [Inf,Inf,2];

Решить проблему с помощью coneprog функция.

[x,fval] = coneprog(f,socConstraints,Aineq,bineq,Aeq,beq,lb,ub)

Optimal solution found.

fval = -8.2462

Компонент решения x(3) находится на верхней границе. Зависимость конуса активна в решении:

norm(A*x-b) - d'*x % Near 0 when the constraint is active

ans = -2.5677e-08

Несколько зависимостей конуса

Открыть сценарий в реальном времени

Чтобы настроить проблему с несколькими зависимостями конуса второго порядка, создайте массив объектов ограничения. Чтобы сэкономить время и память, сначала создайте ограничение с самым высоким индексом.

A = diag([1,2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = -1;
socConstraints(3) = secondordercone(A,b,d,gamma);

A = diag([3,0,1]);
d = [0;1;0];
socConstraints(2) = secondordercone(A,b,d,gamma);

A = diag([0;1/2;1/2]);
d = [1;0;0];
socConstraints(1) = secondordercone(A,b,d,gamma);

Создайте вектор линейной целевой функции.

f = [-1;-2;-4];

Решить проблему с помощью coneprog функция.

[x,fval] = coneprog(f,socConstraints)

Optimal solution found.

fval = -13.0089

Коническое программирование с линейными зависимостями

Открыть сценарий в реальном времени

Укажите вектор целевой функции и одно ограничение конуса второго порядка.

f = [-4;-9;-2];
Asc = diag([1,4,0]);
b = [0;0;0];
d = [0;0;1];
gamma = 0;
socConstraints = secondordercone(Asc,b,d,gamma);

Задайте линейное ограничение неравенства.

A = [1/4,1/9,1];
b = 5;

Решите проблему.

[x,fval] = coneprog(f,socConstraints,A,b)

Optimal solution found.

fval = -26.9225

Коническое программирование с опциями не по умолчанию

Открыть сценарий в реальном времени

Наблюдение за итерациями coneprog решатель, установите Display опция для 'iter'.

options = optimoptions('coneprog','Display','iter');

Создайте проблему программирования конуса второго порядка и решите ее с помощью options.

Asc = diag([1,1/2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = 0;
socConstraints = secondordercone(Asc,b,d,gamma);
f = [-1,-2,0];
Aineq = [];
bineq = [];
Aeq = [];
beq = [];
lb = [-Inf,-Inf,0];
ub = [Inf,Inf,2];
[x,fval] = coneprog(f,socConstraints,Aineq,bineq,Aeq,beq,lb,ub,options)

Iter           Fval  Primal Infeas    Dual Infeas    Duality Gap    Time
   1   0.000000e+00   0.000000e+00   5.714286e-01   1.250000e-01    0.02
   2  -7.558066e+00   0.000000e+00   7.151114e-02   1.564306e-02    0.02
   3  -7.366973e+00   0.000000e+00   1.075440e-02   2.352525e-03    0.02
   4  -8.243432e+00   0.000000e+00   5.191882e-05   1.135724e-05    0.02
   5  -8.246067e+00   1.387779e-17   2.430813e-06   5.317403e-07    0.02
   6  -8.246211e+00   0.000000e+00   6.154504e-09   1.346298e-09    0.03
Optimal solution found.

fval = -8.2462

Конусное программирование с проблемной структурой

Открыть сценарий в реальном времени

Создайте элементы проблемы программирования конуса второго порядка. Чтобы сэкономить время и память, сначала создайте ограничение с самым высоким индексом.

A = diag([1,2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = -1;
socConstraints(3) = secondordercone(A,b,d,gamma);
A = diag([3,0,1]);
d = [0;1;0];
socConstraints(2) = secondordercone(A,b,d,gamma);
A = diag([0;1/2;1/2]);
d = [1;0;0];
socConstraints(1) = secondordercone(A,b,d,gamma);
f = [-1;-2;-4];
options = optimoptions('coneprog','Display','iter');

Создайте структуру проблемы с требуемыми полями, как описано в описании проблемы.

problem = struct('f',f,...
    'socConstraints',socConstraints,...
    'Aineq',[],'bineq',[],...
    'Aeq',[],'beq',[],...
    'lb',[],'ub',[],...
    'solver','coneprog',...
    'options',options);

Решить проблему, позвонив coneprog.

[x,fval] = coneprog(problem)

Iter           Fval  Primal Infeas    Dual Infeas    Duality Gap    Time
   1   0.000000e+00   0.000000e+00   5.333333e-01   5.555556e-02    0.13
   2  -9.696012e+00   1.850372e-17   7.631901e-02   7.949897e-03    0.14
   3  -1.178942e+01   9.251859e-18   1.261803e-02   1.314378e-03    0.14
   4  -1.294426e+01   1.850372e-17   1.683078e-03   1.753206e-04    0.14
   5  -1.295217e+01   1.850372e-17   8.994595e-04   9.369370e-05    0.14
   6  -1.295331e+01   1.850372e-17   4.748841e-04   4.946709e-05    0.15
   7  -1.300753e+01   9.251859e-18   2.799942e-05   2.916606e-06    0.15
   8  -1.300671e+01   9.251859e-18   2.366136e-05   2.464725e-06    0.15
   9  -1.300850e+01   1.850372e-17   8.187205e-06   8.528338e-07    0.15
  10  -1.300843e+01   4.625929e-18   7.326330e-06   7.631594e-07    0.15
  11  -1.300862e+01   9.251859e-18   2.707005e-06   2.819797e-07    0.15
  12  -1.300892e+01   0.000000e+00   9.204457e-08   9.587976e-09    0.15
Optimal solution found.

fval = -13.0089

Исследовать `coneprog` Процесс решения

Открыть сценарий в реальном времени

Создайте проблему программирования конуса второго порядка. Чтобы сэкономить время и память, сначала создайте ограничение с самым высоким индексом.

A = diag([1,2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = -1;
socConstraints(3) = secondordercone(A,b,d,gamma);
A = diag([3,0,1]);
d = [0;1;0];
socConstraints(2) = secondordercone(A,b,d,gamma);
A = diag([0;1/2;1/2]);
d = [1;0;0];
socConstraints(1) = secondordercone(A,b,d,gamma);
f = [-1;-2;-4];
options = optimoptions('coneprog','Display','iter');
A = [];
b = [];
Aeq = [];
beq = [];
lb = [];
ub = [];

Решите проблему, запросив информацию о процессе решения.

[x,fval,exitflag,output] = coneprog(f,socConstraints,A,b,Aeq,beq,lb,ub,options)

Iter           Fval  Primal Infeas    Dual Infeas    Duality Gap    Time
   1   0.000000e+00   0.000000e+00   5.333333e-01   5.555556e-02    0.04
   2  -9.696012e+00   1.850372e-17   7.631901e-02   7.949897e-03    0.06
   3  -1.178942e+01   9.251859e-18   1.261803e-02   1.314378e-03    0.06
   4  -1.294426e+01   1.850372e-17   1.683078e-03   1.753206e-04    0.06
   5  -1.295217e+01   1.850372e-17   8.994595e-04   9.369370e-05    0.06
   6  -1.295331e+01   1.850372e-17   4.748841e-04   4.946709e-05    0.06
   7  -1.300753e+01   9.251859e-18   2.799942e-05   2.916606e-06    0.06
   8  -1.300671e+01   9.251859e-18   2.366136e-05   2.464725e-06    0.06
   9  -1.300850e+01   1.850372e-17   8.187205e-06   8.528338e-07    0.06
  10  -1.300843e+01   4.625929e-18   7.326330e-06   7.631594e-07    0.06
  11  -1.300862e+01   9.251859e-18   2.707005e-06   2.819797e-07    0.06
  12  -1.300892e+01   0.000000e+00   9.204457e-08   9.587976e-09    0.06
Optimal solution found.

fval = -13.0089

exitflag = 1

output = struct with fields:
           iterations: 12
    primalfeasibility: 0
      dualfeasibility: 9.2045e-08
           dualitygap: 9.5880e-09
            algorithm: 'interior-point'
         linearsolver: 'augmented'
              message: 'Optimal solution found.'

Итеративное отображение и структура вывода показывают, что coneprog использовал 12 итераций для получения решения.
Значение флага выхода 1 и output.message стоимость 'Optimal solution found.' указать, что решение является надежным.
output структура показывает, что несходимости имеют тенденцию уменьшаться в процессе решения, как и разрыв двойственности.
Вы можете воспроизвести fval вывод путем умножения f'*x.

f'*x

ans = -13.0089

Получить `coneprog` Двойные переменные

Открыть сценарий в реальном времени

A = diag([1,2,0]);
b = zeros(3,1);
d = [0;0;1];
gamma = -1;
socConstraints(3) = secondordercone(A,b,d,gamma);
A = diag([3,0,1]);
d = [0;1;0];
socConstraints(2) = secondordercone(A,b,d,gamma);
A = diag([0;1/2;1/2]);
d = [1;0;0];
socConstraints(1) = secondordercone(A,b,d,gamma);
f = [-1;-2;-4];

Решите проблему, запросив двойные переменные в решении вместе со всеми другими coneprog выход..

[x,fval,exitflag,output,lambda] = coneprog(f,socConstraints);

Optimal solution found.

Проверьте возвращенные lambda структура. Поскольку единственной проблемой являются ограничения конуса, проверьте только soc в поле lambda структура.

disp(lambda.soc)

Ограничения имеют ненулевые двойственные значения, указывающие на то, что ограничения активны в решении.

Входные аргументы

свернуть все

`f` - Вектор коэффициентов
вещественный вектор | вещественный массив

Вектор коэффициента, заданный как действительный вектор или вещественный массив. Вектор коэффициентов представляет целевую функцию f'*x. Запись предполагает, что f является вектором столбца, но можно использовать вектор строки или массив. Внутри, coneprog новообращенные f к вектору столбца f(:).

Пример: f = [1,3,5,-6]

Типы данных: double

`socConstraints` - Ограничения конуса второго порядка
вектор `SecondOrderConeConstraint` объекты

Ограничения конуса второго порядка, заданные как вектор SecondOrderConeConstraint объекты. Создайте эти объекты с помощью secondordercone функция.

socConstraints кодирует ограничения

$‖_{} Asc (i)_{} \cdotx-bsc (i_{)}^{‖} \leqdscT (i)$ ⋅x−γ (i)

где отображение между массивом и уравнением выглядит следующим образом:

Asc (i) =socConstraints.A(i)
bsc (i) =socConstraints.b(i)
dsc (i) =socConstraints.d(i)
γ (i) =socConstraints.gamma(i)

Пример: Asc = diag([1 1/2 0]); bsc = zeros(3,1); dsc = [0;0;1]; gamma = -1; socConstraints = secondordercone(Asc,bsc,dsc,gamma);

Типы данных: struct

`A` - Линейные ограничения неравенства
реальная матрица

Линейные ограничения неравенства, заданные как вещественная матрица. A является Mоколо-N матрица, где M - количество неравенств, и N - количество переменных (длина f). По большим проблемам проходите A в виде разреженной матрицы.

A кодирует M линейные неравенства

A*x <= b,

где x - вектор столбца N переменные x(:), и b - вектор столбца с M элементы.

Например, рассмотрим эти неравенства:

x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30.

Задайте неравенства, введя следующие ограничения.

A = [1,2;3,4;5,6];
b = [10;20;30];

Пример: Чтобы указать, что x-компоненты складываются до 1 или менее, возьмите A = ones(1,N) и b = 1.

Типы данных: double

`b` - Линейные ограничения неравенства
действительный вектор

Линейные ограничения неравенства, заданные как действительный вектор. b является M-элементный вектор, связанный с A матрица. Если вы проходите b как вектор строки, решатели внутренне преобразуют b к вектору столбца b(:). По большим проблемам проходите b как разреженный вектор.

b кодирует M линейные неравенства

A*x <= b,

где x - вектор столбца N переменные x(:), и A является матрицей размера Mоколо-N.

Например, рассмотрим эти неравенства:

x1 + 2x2 ≤ 10
3x1 + 4x2 ≤ 20
5x1 + 6x2 ≤ 30.

Задайте неравенства, введя следующие ограничения.

A = [1,2;3,4;5,6];
b = [10;20;30];

Пример: Чтобы указать, что компоненты x суммируются до 1 или менее, используйте A = ones(1,N) и b = 1.

Типы данных: double

`Aeq` - Линейные ограничения равенства
реальная матрица

Линейные ограничения равенства, заданные как вещественная матрица. Aeq является Meоколо-N матрица, где Me - количество уравнений, и N - количество переменных (длина f). По большим проблемам проходите Aeq в виде разреженной матрицы.

Aeq кодирует Me линейные равенства

Aeq*x = beq,

где x - вектор столбца N переменные x(:), и beq - вектор столбца с Me элементы.

Например, рассмотрим следующие равенства:

x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20.

Задайте равенства, введя следующие ограничения.

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Пример: Чтобы указать, что x-компоненты суммируются до 1, возьмите Aeq = ones(1,N) и beq = 1.

Типы данных: double

`beq` - Линейные ограничения равенства
действительный вектор

Линейные ограничения равенства, заданные как действительный вектор. beq является Me-элементный вектор, связанный с Aeq матрица. Если вы проходите beq как вектор строки, решатели внутренне преобразуют beq к вектору столбца beq(:). По большим проблемам проходите beq как разреженный вектор.

beq кодирует Me линейные равенства

Aeq*x = beq,

где x - вектор столбца N переменные x(:), и Aeq является матрицей размера Meоколо-N.

Например, рассмотрим следующие равенства:

x1 + 2x2 + 3x3 = 10
2x1 + 4x2 + x3 = 20.

Задайте равенства, введя следующие ограничения.

Aeq = [1,2,3;2,4,1];
beq = [10;20];

Пример: Чтобы указать, что компоненты x суммируются до 1, используйте Aeq = ones(1,N) и beq = 1.

Типы данных: double

`lb` - Нижние границы
вещественный вектор | вещественный массив

Нижние границы, определяемые как вещественный вектор или вещественный массив. Если длина f равна длине lb, то lb указывает, что

x(i) >= lb(i) для всех i.

Если numel(lb) < numel(f), то lb указывает, что

x(i) >= lb(i) для 1 <= i <= numel(lb).

В этом случае решатели выдают предупреждение.

Пример: Чтобы указать, что все компоненты X являются положительными, используйте lb = zeros(size(f)).

Типы данных: double

`ub` - Верхние границы
вещественный вектор | вещественный массив

Верхние границы, заданные как вещественный вектор или вещественный массив. Если длина f равна длине ub, то ub указывает, что

x(i) <= ub(i) для всех i.

Если numel(ub) < numel(f), то ub указывает, что

x(i) <= ub(i) для 1 <= i <= numel(ub).

В этом случае решатели выдают предупреждение.

Пример: Чтобы указать, что все компоненты X меньше 1, использовать ub = ones(size(f)).

Типы данных: double

`options` - Варианты оптимизации
вывод `optimoptions`

Опции оптимизации, указанные как выходные данные optimoptions.

Выбор	Описание
`ConstraintTolerance`	Допуск выполнимости для ограничений, скаляр из `0` через `1`. `ConstraintTolerance` измеряет предельно допустимую осуществимость. Значение по умолчанию: `1e-6`.
`Display`	Уровень отображения (см. Итерационный просмотр): `'final'` (по умолчанию) отображает только окончательный вывод. `'iter'` отображает выходные данные в каждой итерации. `'off'` или `'none'` не отображает выходные данные.
`LinearSolver`	Алгоритм решения одного шага итерации: `'auto'` (по умолчанию) - `coneprog` выбирает решатель шагов. Если проблема разрежена, решателем шага является `'prodchol'`. В противном случае решателем шага является `'augmented'`. `'augmented'` - Решатель шагов дополненной формы. См. [1]. `'normal'` - Стандартный решатель шагов формы. См. [1]. `'prodchol'` - Форма продукта Cholesky шагового решателя. См. разделы [4] и [5]. `'schur'` - решатель шагов метода дополнения Шура. См. [2]. Если `'auto'` не работает хорошо, попробуйте эти предложения для `LinearSolver`: Если проблема разрежена, попробуйте `'normal'`. Если проблема разрежена с некоторыми плотными колоннами или большими конусами, попробуйте `'prodchol'` или `'schur'`. Если проблема является плотной, используйте `'augmented'`. Разреженный пример см. в разделе Сравнение скоростей алгоритмов coneprog.
`MaxIterations`	Максимальное допустимое число итераций, положительное целое число. Значение по умолчанию: `200`. См. раздел Допуски и критерии остановки, итерации и подсчеты функций.
`MaxTime`	Максимальное время в секундах выполнения алгоритма, положительное число или `Inf`. Значение по умолчанию: `Inf`, что отключает этот критерий остановки.
`OptimalityTolerance`	Допуск окончания для двойной осуществимости, положительный скаляр. Значение по умолчанию: `1e-6`.

Пример: optimoptions('coneprog','Display','iter','MaxIterations',100)

`problem` - Структура проблемы
структура

Структура проблемы, заданная как структура со следующими полями.

Имя поля	Вход
`f`	Вектор линейной целевой функции `f`
`socConstraints`	Структурный массив ограничений конуса второго порядка
`Aineq`	Матрица линейных ограничений неравенства
`bineq`	Вектор линейных ограничений неравенства
`Aeq`	Матрица линейных ограничений равенства
`beq`	Вектор линейных ограничений равенства
`lb`	Вектор нижних границ
`ub`	Вектор верхних границ
`solver`	`'coneprog'`
`options`	Параметры, созданные с помощью `optimoptions`

Типы данных: struct

Выходные аргументы

свернуть все

`x` - Решение
вещественный вектор | вещественный массив

Решение, возвращаемое в виде вещественного вектора или вещественного массива. Размер x совпадает с размером f. x выходной сигнал пуст, если exitflag значение равно -2, –3, или -10.

`fval` - Значение целевой функции при решении
вещественное число

Значение целевой функции в решении, возвращаемое как вещественное число. Как правило, fval = f'*x. fval выходной сигнал пуст, если exitflag значение равно -2, –3, или -10.

`exitflag` - Причина `coneprog` остановленный
целое число

Причина coneprog остановлено, возвращено как целое число.

Стоимость	Описание
`1`	Функция сходилась к решению `x`.
`0`	Превышено число итераций `options.MaxIterations`или превышено время решения в секундах `options.MaxTime`.
`-2`	Выполнимая точка не найдена.
`-3`	Проблема безгранична.
`-7`	Направление поиска стало слишком маленьким. Дальнейшего прогресса достичь не удалось.
`-10`	Проблема численно нестабильна.

Совет

Если вы получаете флаг выхода 0, -7, или -10, попробуйте использовать другое значение LinearSolver вариант.

`output` - Информация о процессе оптимизации
структура

Информация о процессе оптимизации, возвращенная в виде структуры с этими полями.

Область	Описание
`algorithm`	Используемый алгоритм оптимизации
`dualfeasibility`	Максимум нарушений двойного ограничения
`dualitygap`	Разрыв двойственности
`iterations`	Количество итераций
`message`	Выйти из сообщения
`primalfeasibility`	Максимум нарушений ограничений
`linearsolver`	Используемый алгоритм внутреннего решателя шагов

output области dualfeasibility, dualitygap, и primalfeasibility пусты, когда exitflag значение равно -2, -3 или -10.

`lambda` - Двойные переменные в решении
структура

Двойные переменные в решении, возвращаемые в виде структуры с этими полями.

Область	Описание
`lower`	Нижние границы, соответствующие `lb`
`upper`	Верхние границы, соответствующие `ub`
`ineqlin`	Линейные неравенства, соответствующие `A` и `b`
`eqlin`	Линейные равенства, соответствующие `Aeq` и `beq`
`soc`	Ограничения конуса второго порядка, соответствующие `socConstraints`

lambda пуст ([]), когда exitflag значение равно -2, –3, или -10.

Множители Лагранжа (двойственные переменные) являются частью следующего Лагранжиана, который является стационарным (нулевой градиент) при решении:

$\begin{array}{l} ^{} \underset{}{}_{fTx+∑iλsoc} (i)_{(}^{} dsocT (i) x − {гамма}_{(i})_{−‖Asoc} (i) x \\ − bsoc_{(i) ‖)}^{+ (}_{b}^{-} Ax) + (_{Aeq}^{} x - {beq}_{) + (}^{} ub \end{array}$ − x) + (x − lowerT).

Условия неравенства, которые умножают lambda поля неотрицательны.

Подробнее

свернуть все

Ограничение конуса второго порядка

Почему ограничение

$^{} ‖A⋅x−b dTx−γ$

называется ограничением конуса второго порядка? Рассмотрим конус в 3-D пространстве с эллиптическими поперечными сечениями в плоскости x-y и диаметром, пропорциональным координате z. Координата y имеет масштаб ½, а координата x - масштаб 1. Неравенство, определяющее внутреннюю часть этого конуса с его точкой в [0,0,0], равно

$\sqrt{^{} \frac{^{}}{}} x2+y24≤z .$

В coneprog , этот конус имеет следующие аргументы.

A = diag([1 1/2 0]);
b = [0;0;0];
d = [0;0;1];
gamma = 0;

Постройте график границы конуса.

[X,Y] = meshgrid(-2:0.1:2);
Z = sqrt(X.^2 + Y.^2/4);
surf(X,Y,Z)
view(8,2)
xlabel 'x'
ylabel 'y'
zlabel 'z'

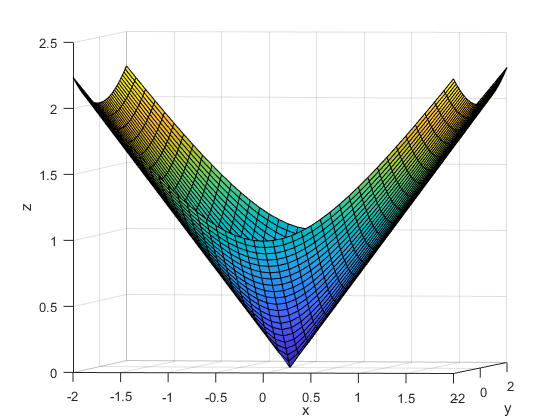
b и gamma аргументы перемещают конус. A и d аргументы поворачивают конус и изменяют его форму.

Алгоритмы

Алгоритм использует метод внутренней точки. Дополнительные сведения см. в разделе Алгоритм программирования конуса второго порядка.

Альтернативная функциональность

Приложение

Задача «Оптимизировать интерактивный редактор» обеспечивает визуальный интерфейс для coneprog.

Вопросы совместимости

развернуть все

Два `coneprog` `lambda` Структуры переименованы

В R2021a изменилось поведение

coneprog lambda поля выходных аргументов lambda.eq и lambda.ineq были переименованы в lambda.eqlin и lambda.ineqlinсоответственно. Это изменение вызывает coneprog lambda поля структуры должны иметь те же имена, что и соответствующие поля в других решателях.

См. также

linprog | Оптимизировать | quadprog | secondordercone | SecondOrderConeConstraint

Темы

Представлен в R2020b

Документация

coneprog

Синтаксис

Описание

Примеры

Зависимость «Один конус»

Несколько зависимостей конуса

Коническое программирование с линейными зависимостями

Коническое программирование с опциями не по умолчанию

Конусное программирование с проблемной структурой

Исследовать `coneprog` Процесс решения

Получить `coneprog` Двойные переменные

Входные аргументы

`f` - Вектор коэффициентов
вещественный вектор | вещественный массив

`socConstraints` - Ограничения конуса второго порядка
вектор `SecondOrderConeConstraint` объекты

`A` - Линейные ограничения неравенства
реальная матрица

`b` - Линейные ограничения неравенства
действительный вектор

`Aeq` - Линейные ограничения равенства
реальная матрица

`beq` - Линейные ограничения равенства
действительный вектор

`lb` - Нижние границы
вещественный вектор | вещественный массив

`ub` - Верхние границы
вещественный вектор | вещественный массив

`options` - Варианты оптимизации
вывод `optimoptions`

`problem` - Структура проблемы
структура

Выходные аргументы

`x` - Решение
вещественный вектор | вещественный массив

`fval` - Значение целевой функции при решении
вещественное число

`exitflag` - Причина `coneprog` остановленный
целое число

`output` - Информация о процессе оптимизации
структура

`lambda` - Двойные переменные в решении
структура

Подробнее

Ограничение конуса второго порядка

Алгоритмы

Альтернативная функциональность

Приложение

Вопросы совместимости

Два `coneprog` `lambda` Структуры переименованы

См. также

Темы

Документация по панели инструментов оптимизации

Поддержка

Документация

coneprog

Синтаксис

Описание

Примеры

Зависимость «Один конус»

Несколько зависимостей конуса

Коническое программирование с линейными зависимостями

Коническое программирование с опциями не по умолчанию

Конусное программирование с проблемной структурой

Исследовать coneprog Процесс решения

Получить coneprog Двойные переменные

Входные аргументы

f - Вектор коэффициентов вещественный вектор | вещественный массив

socConstraints - Ограничения конуса второго порядка вектор SecondOrderConeConstraint объекты

A - Линейные ограничения неравенства реальная матрица

b - Линейные ограничения неравенства действительный вектор

Aeq - Линейные ограничения равенства реальная матрица

beq - Линейные ограничения равенства действительный вектор

lb - Нижние границы вещественный вектор | вещественный массив

ub - Верхние границы вещественный вектор | вещественный массив

options - Варианты оптимизации вывод optimoptions

problem - Структура проблемы структура

Выходные аргументы

x - Решение вещественный вектор | вещественный массив

fval - Значение целевой функции при решении вещественное число

exitflag - Причина coneprog остановленный целое число

output - Информация о процессе оптимизации структура

lambda - Двойные переменные в решении структура

Подробнее

Ограничение конуса второго порядка

Алгоритмы

Альтернативная функциональность

Приложение

Вопросы совместимости

Два coneprog lambda Структуры переименованы

См. также

Темы

Документация по панели инструментов оптимизации

Поддержка

Исследовать `coneprog` Процесс решения

Получить `coneprog` Двойные переменные

`f` - Вектор коэффициентов
вещественный вектор | вещественный массив

`socConstraints` - Ограничения конуса второго порядка
вектор `SecondOrderConeConstraint` объекты

`A` - Линейные ограничения неравенства
реальная матрица

`b` - Линейные ограничения неравенства
действительный вектор

`Aeq` - Линейные ограничения равенства
реальная матрица

`beq` - Линейные ограничения равенства
действительный вектор

`lb` - Нижние границы
вещественный вектор | вещественный массив

`ub` - Верхние границы
вещественный вектор | вещественный массив

`options` - Варианты оптимизации
вывод `optimoptions`

`problem` - Структура проблемы
структура

`x` - Решение
вещественный вектор | вещественный массив

`fval` - Значение целевой функции при решении
вещественное число

`exitflag` - Причина `coneprog` остановленный
целое число

`output` - Информация о процессе оптимизации
структура

`lambda` - Двойные переменные в решении
структура

Два `coneprog` `lambda` Структуры переименованы